この冬休みに、選択公理bot(@AxiomderAuswahl)を再始動させました。
選択公理botはC#で書かれていて(最初はPHPでしたが…)、.NET Frameworkにより動いていました。それはつまりwindowsサーバー上で動いていたということです。windowsサーバーは(ライセンス料などもあって?)高いのですが、なんと月額250円(?!)のwindowsレンタルサーバーが以前あったのでそれを使っていました。ところが流石に安すぎたのかサービス終了、それに伴い選択公理botも停止状態となっていました。
ところで何年か前から.NET Frameworkをwindows以外でも動かせるようにしようという動きがあり、それが.NET Coreと呼ばれるものです。その最新バージョンである.NET 5が2020年11月にリリースされました。(.NET 5は.NET Frameworkの次期バージョンでもあります。)選択公理botはこの.NET 5を使い、Ubuntuサーバー上で動かしています。基本的には.NET Frameworkのときとほぼ同じソースコードで、対象フレームワークを.NET 5に変えただけで動いています。
実際にやり方についてはMicorsoftの公式ドキュメントが詳しいです(Nginx 搭載の Linux で ASP.NET Core をホストする)。また選択公理botのような、定期的に実行するようなものについても公式が参考になります(ASP.NET Core でホステッド サービスを使用するバックグラウンド タスク)。
また今回、リプライへの反応についてはTwitterの新しいAPIを使用するようにしました。webhookと言われているやつです。これはQiitaの記事が参考になります(【エラーコード別解説】Twitter の Account Activity API の Webhook URL が登録できないときの解決法)。
この前2019をインストールしたばかりな気がしますが、TeX Live 2020が出たのでインストールしました。やり方はいつもと同じ感じなので省略します
さて、インストール自体はこれで良かったのですが、TeX Live 2019以前をインストール済みでtexmf-localフォルダを使用していた場合、恐らくエラーが発生するようになると思います。このフォルダの権限設定がTeX Live 2020によって変更されてしまう(?)ようです。
権限周りの設定のことがよくわからないので、僕は必要なファイルを一個ずつ右クリックして権限を付けて回りました……
前回の通り、パソコンを新しくしたのでTeXの環境も整え直します。TeX Live 2019を入れる話は以前に書いた通りで、今回はエラーもなく1時間半程度で終わりました。
現在公開しているPDFファイルはフォントとして源ノ明朝というものを使っているので、これも入れます。これはZRさんのupLaTeX文書で源ノ明朝/Noto Serif CJKを簡単に使う方法(最新のdvipdfmxとpxchfonを使用)の通りで、要はWindows10に対して源ノ明朝というフォントをインストールすれば、あとは記事の通りTeXファイルを書くだけです。が、前のPCではこれでうまくいっていたのに今回はうまく動きませんでした。
調べた結果、Windows10 (のバージョン1809以降)ではフォントをインストールする際に「ユーザーごと」「全ユーザー」という2種類のインストール方法があり、「ユーザーごと」のインストールだとTeXではダメなようです(参考サイト: Windows 10にフォントを追加インストールする方法と注意点)。前のPCでフォントを入れたときは1809より前のバージョンで、エラーにならなかったのかもしれません。
というわけで、全ユーザーに対してフォントをインストールしなおすことで、無事に源ノ明朝が使えるようになりました。
実は今使っているパソコンは2016年1月頃に買ったものですが、なんか調子が悪いです。
まず、一年前くらいにこのパソコンは壊れました。↓当時のツイート
何が悪いのかはよく分かりませんが、とりあえずメモリを買って来て交換したら無事動きました。
(このとき実は最初に「とりあえずメモリ片方抜いてみたら」とアドバイスを貰ったのですが、このパソコンはメモリは8GB1枚だったのです。こういうときに困るということが分かったので今後は必ず2枚組にします。)
でまぁこのときはこれで治ったのですが、それから1年経った先日、また同じような現象が発生しました。今度はメモリを片方ずつ抜いて試したところ、正常に起動したので、またメモリが悪かったらしいと分かりました。
しかし……メモリって1年でそんな簡単に壊れるのか? 別の場所に根本的な原因があるのでは? とか、そもそもパソコンの調子が全体的に悪い感じがする(再起動にすごい時間かかるし…)とかで、なんかもう今使ってるパソコンが全然信用できない感じになってしまいました。
そこで、新しいパソコンを購入しました!! (続く?)
TeX Liveインストールチャレンジ2019をしました。手順は昨年と大体同じです。
- TeX Liveのページに行きdownloadのページから install-tl-windows.exe をDLします。
- DLした install-tl-windows.exe を実行する(後述するように右クリックして「管理者として実行」した方が良いと思います)と次の画面が表示されるので、「Next」をクリックします。
- すると次の画面が表示されるので、「Install」をクリックすると
- インストールっぽいことが始まります。
- ちょっと待つとこんな画面が出てきて
さらにこの画面に変わります。
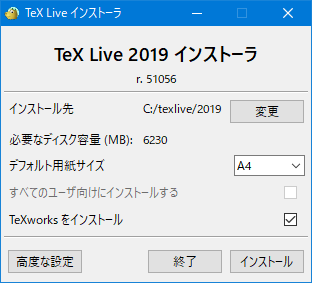
ここで、この画像だと「すべてのユーザ向けにインストールする」がグレーアウトしていて、チェック不可になっています。これは恐らくインストーラを管理者権限で実行していないからで、install-tl-windows.exe を右クリックして「管理者として実行」すればチェックがONにできるようになります。
- 好みの設定にしたら「インストール」をクリックすると、いつものようにインストールが始まります。
- これが終わるとこの画面になるので
「閉じる」をクリックすると次の画面になります。
- 「Close」をクリックしてインストール完了です。
で、うまく行くんですか? と思っている人もいるかもしれません。今年はなんと、1回目はエラーが出て失敗しましたが2回目で成功しました。成功したので昨年と同様、コマンドプロンプトを開いて「tex -version」とやってみると、確かにTeX Live 2019と出、ま、せん……。
で調べて分かったのが上記の「すべてのユーザ向けにインストールする」の話です。TeX Live 2018をインストールすると、システム環境変数のPathに必要な設定がされますが、TeX Live 2019のインストールを「すべての(ry」チェックOFFでやってしまうとユーザ環境変数の方にPathが設定されるようです(チェックONでインストールは試してないので、実際どうなのかは分かりませんが)。Windows10の仕様ではPathはシステム環境変数の方が優先される(正確な書き方ではないので、気になる人は調べてください)ようなので、これではtexを実行した時にTeX Live 2018の方が実行されてしまうわけです。
というわけで、環境変数を手で設定し直したところ、無事「tex -version」でTeX Live 2019と出るようになりました。
(2019/08/26追記: 「すべての(ry」チェックONでインストールするとシステム環境変数のPathに必要な設定がされることを確認しました。)
(2019/08/26追記その2: Windows10+upLaTeXで源ノ明朝を使う
も参考にしてください。)










