集合に関する命題

定理1 選択公理
⇔ 非空集合の族 ${X_λ}_{λ∈Λ}$ で全てのX_λの濃度が等しいもの，に対して $Π_{λ∈Λ}X_λ$ ≠ ∅

証明⇒ は明らかなので，逆を示せばよい． ${X_λ}_{λ∈Λ}$ を非空集合の任意の族とする．Y := ( $∪_{λ∈Λ}X_λ$ )^Nと置く．明らかに Y≠∅ である．λ∈Λに対し F_λ: Y×X_λ→Y を

F_λ(f, x)(0) := x
F_λ(f, x)(n+1) := f(n)

で定義する．F_λ は単射だから |Y×X_λ|≦|Y|．|Y|≦|Y×X_λ| だからBernsteinの定理より |Y×X_λ| = |Y|．従って仮定から Π_λ∈Λ(Y×X_λ) ≠ ∅．故に $Π_{λ∈Λ}X_λ$ ≠ ∅である．

この証明で，選択関数の存在が非自明な場合には |Y|=∞ となるから，次の系が分かる．

系2 選択公理
⇔ 無限集合の族 { X_λ }_λ∈Λ で全ての X_λ の濃度が等しいもの，に対して Π_λ∈ΛX_λ≠ ∅

定理3 選択公理
⇔ 集合の順序対からなる族 { <X_λ, Y_λ> }_λ∈Λが，各λ∈Λに対し |X_λ| = |Y_λ| を満たしているとする．このとき写像の族 {f_λ}_λ∈Λ で，「各λ∈Λに対し f_λ: X_λ→Y_λ は全単射」を満たすものが存在する．

証明 ⇒は明らかなので，逆を示せばよい． ${X_λ}_{λ∈Λ}$ を非空集合の任意の族とする．| X_λ×N | = | X_λ×N∪{ ∅ } | であるから，族 { <X_λ×N∪{ ∅ }, X_λ×N> }_λ∈Λに仮定を適用して全単射 f_λ: X_λ×N∪{ ∅ }→X_λ×N からなる族を得る．g(λ) := ( f_λ( ∅ )の第一成分 ) と置けば，gが選択関数である．

定理4 選択公理
⇔ 非空集合の族 ${X_λ}_{λ∈Λ}$ は全てのX_λの濃度が等しいとする．このとき写像の族{ f_{λ, μ} }_{λ, μ∈Λ}で，「各λ, μ∈Λに対し f_{λ, μ}: X_λ→X_μ は全単射」を満たすものが存在する．

証明 ⇒ は明らかなので，逆を示せばよい． ${X_λ}_{λ∈Λ}$ を非空集合の任意の族とする．Y := ( $∪_{λ∈Λ}X_λ$ )^N と置く．明らかにY≠ ∅ である．定理1の証明と同様にして | X_λ×Y | = |Y| が分かる．また，| X_λ×Y | = | X_λ×Y∪{ ∅ } | も容易に分かる．

I := {0}×Λ, J := {1}×Λ, K := I∪K と置き <0, λ>∈I に対し Y_{<0, λ>} := X_λ×Y∪{ ∅ }, <1, λ>∈J に対しY_{<1, λ>} := X_λ×Y と定める．族{ Y_i }_i∈K に仮定を適用して全単射の族 { f_{i, j} }_{i, j∈K} を得る．このとき各λ∈Λに対し

F_λ := f_{<0, λ>, <1, λ>}: X_λ×Y∪{ ∅ }→X_λ×Y

は全単射である．そこでg(λ) := ( F_λ( ∅ )の第一成分 ) と置けば，gが選択関数である．

集合 X に対して Aut(X) := { f: X→X | f は全単射 } とおく．

定理5 選択公理
⇔ 非空集合の族 { X_λ } _λ∈Λ は全ての X_λ の濃度が等しいとする．このときある λ₀∈Λ と写像の族 { f_λ } _λ∈Λ が存在して「各 λ∈Λ に対して f_λ: Aut(X_λ₀)→Aut(X_λ) は群同型」を満たす．

証明 ⇒ は明らかなので， ⇐ を示せばよい．その為には系2の条件を示せばよい．

その為に以下の事実を思い出しておく． X を集合とする． g∈Aut(X) に対して supp(g) := { x∈X | g(x)≠x } と置く． g が互換であるとは， |supp(g)| = 2 となることである． X, Y を無限集合とする． f: Aut(X)→Aut(Y) が群同型のとき， g∈Aut(X) が互換ならば f(g)∈Aut(Y) も互換である．また，二つの互換 g, h∈Aut(X) が交換不可能である為の必要十分条件は |supp(g)∩supp(h)| = 1 となることである．

さて， ${X_λ}_{λ∈Λ}$ を無限集合の族で， λ≠μ ならば |X_λ| = |X_μ| であるとする．仮定により λ₀∈Λ と写像の族 { f_λ }_λ∈Λ が存在して「各 λ∈Λ に対して f_λ: Aut(X_λ₀)→Aut(X_λ) は群同型」となる．元 x, y, z∈X_λ₀ を取り， g∈Aut(X_λ₀) を「 x, y を入れ替える互換」， h∈Aut(X_λ₀) を「 x, z を入れ替える互換」とする．このとき λ∈Λ に対して supp(f_λ(g))∩supp(f_λ(h)) = { x_λ } となる x_λ が一意に取れる．これにより Π_λ∈ΛX_λ≠ ∅ である．

補題6 ${X_λ}_{λ∈Λ}$ と { Y_λ }_λ∈Λ が $Π_{λ∈Λ}X_λ$ = Π_λ∈ΛY_λ≠ ∅ を満たすならば，各 λ∈Λ について X_λ=Y_λ となる．

証明 x = (x_λ)_λ∈Λ∈Π_λ∈ΛX_λ を一つ取る． μ∈Λ に対して X_μ=Y_μ を示す．その為に a∈X_μ を取り

y_λ := a　(λ=μのとき)
y_λ := x_λ　(λ≠μのとき)

とすれば (y_λ)_λ∈Λ∈Π_λ∈ΛX_λ = Π_λ∈ΛY_λ であるから a∈Y_μ である．故に X_μ⊂Y_μ であり，逆も同様であるから X_μ=Y_μ が分かる．

定理7 選択公理
⇔ 非空集合の族 ${X_λ}_{λ∈Λ}$ ，{ Y_λ }_λ∈Λ が $Π_{λ∈Λ}X_λ$ = Π_λ∈ΛY_λ を満たすならば，各λ∈Λについて X_λ=Y_λ となる．

証明 ( ⇒ ) 選択公理により $Π_{λ∈Λ}X_λ$ ≠ ∅ だから補題6より明らか．

( ⇐ ) ${X_λ}_{λ∈Λ}$ を非空集合の族とする． $Π_{λ∈Λ}X_λ$ = ∅ と仮定する． |X_μ|≧2 となる μ∈Λ を一つ取り， a∈X_μ を取る．非空集合の族 { Y_λ }_λ∈Λ を

Y_λ := X_λ＼{ a }　(λ=μのとき)
Y_λ := X_λ　(λ≠μのとき).

により定めれば Π_λ∈ΛY_λ⊂Π_λ∈ΛX_λ = ∅ により Π_λ∈ΛY_λ = Π_λ∈ΛX_λ である．よって仮定により X_μ = Y_μ = X_μ＼{ a } となり矛盾する．

定理8 以下の命題は(ZF上)同値．

選択公理
任意の X≠∅ と写像 F: X→Y に対して写像 G: Y→X が存在して FGF = F となる．
任意の全射 F: X→Y に対して，ある G: Y→X が存在して FG = id_Y．
任意の二項関係 R⊂X×Y に対して，ある関数 f が存在して dom(R) = dom(f) かつ f⊂R となる．
二項関係 R⊂X×Xが「任意のx∈Xに対してあるy∈Xが存在してxRy」を満たすとき，写像 f: X→X で「任意のx∈Xに対してxRf(x)」を満たすものが存在する．

証明 (1 ⇒ 2) X≠ ∅ , F: X→Y とする．Z := Im(F) と置く．各 y∈Z について F^-1(y) ≠ ∅ である．よって { F^-1(y) }_y∈Z に選択公理を適用して選択関数 f: Z→∪_y∈ZF^-1(y)=X を得る．y∈Z に対し f(y)∈F^-1(y)，即ち F(f(y))=y である．また X≠ ∅ だから，X から1つ元 a∈X が取れる．写像 G: Y→ X を

y∈Z のとき G(y) := f(y)
y ∉ Z のとき G(y) := a

と定義すれば，任意の元x∈Xに対し

FGF(x) = F(G(F(x))) = F(f(F(x))) = F(x)

(2 ⇒ 3) F: X→Y を全射とする．X = ∅ のときは自明なので X≠ ∅ とする．すると仮定2 よりある写像 G: Y→X があって FGF = F = (id_Y)F．よって F の全射性から FG = id_Y である．

(3⇒4) R⊂X×X を二項関係とする．写像 π_X: R→dom(R) を π_X(x, y) := x で定めればπ_Xは全射である．故に仮定3から，π_Xg = id となる写像 g: dom(R)→R が存在する．このとき π_Y: R→Y をπ_Y(x, y) := y で定めて f := π_Ygとすれば f⊂R である．

(4 ⇒ 5) 明らか．

(5 ⇒ 1) ${X_λ}_{λ∈Λ}$ を非空集合の族とする．X := Λ∪ $∪_{λ∈Λ}X_λ$ と置く．Λ∩ $∪_{λ∈Λ}X_λ$ =∅ としてよい．X上の二項関係Rを

aRb ⇔ a∈Λ, b∈X_a または a=b∈ $∪_{λ∈Λ}X_λ$

で定める．このRに仮定5 を適用し，写像f: X→X を得る．g を f をΛに制限した写像を g とすれば，明らかに g: Λ→X は選択関数である．

定理9 次の命題は(ZF上)同値．

選択公理，即ち
非空集合の族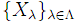 ${X_λ}_{λ∈Λ}$ に対して，ある写像 f: Λ→ 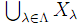$∪_{λ∈Λ}X_λ$ が存在して，任意のλ∈Λに対して f(λ)∈X_λ
集合族 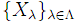${X_λ}_{λ∈Λ}$ に対して，ある写像g: 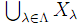$∪_{λ∈Λ}X_λ$ →Λが存在して，任意の x∈ 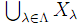$∪_{λ∈Λ}X_λ$ に対して x∈X_g(x)．
集合族 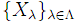${X_λ}_{λ∈Λ}$ に対して，互いに素な集合族{Y_λ}_λ∈Λが存在して Y_λ⊂X_λ, ∪_λ∈ΛY_λ=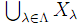 $∪_{λ∈Λ}X_λ$ を満たす．

証明(1 ⇒ 2) $X:=∪_{λ∈Λ}X_λ$ と置き，x∈Xに対し A_x := {λ∈Λ| x∈X_λ }≠∅ と定める．{ A_x }_x∈X に選択公理を適用し，選択関数 g: X→∪_x∈XA_x⊂Λを得る．この g は x∈X_g(x) を満たす．

(2 ⇒ 3) ${X_λ}_{λ∈Λ}$ を集合族とする．仮定2によりg: $∪_{λ∈Λ}X_λ$ →Λで「任意のx∈ $∪_{λ∈Λ}X_λ$ に対してx∈X_g(x)」を満たすものが取れる． Y_λ:=g^-1(λ)とすれば明らかに∪_λ∈ΛY_λ=XかつY_λ∩Y_μ = ∅ (λ≠μ)である．y∈Y_λとするとg(y)=λだから y∈X_g(y) = X_λ．よってY_λ⊂X_λとなる．

(3 ⇒ 1) 定理8の条件3を示す．F: A→B を全射とする．a∈A に対し X_a := { F(a) } と置き，族 { X_a }_a∈A に仮定を適用して Y_a⊂X_a, ∪_a∈A Y_a = ∪_a∈AX_a (=B), Y_a∩Y_b = ∅　(a≠b) を満たす { Y_a }_a∈A を得る．各 b∈B に対して b∈Y_G(b) となる G(b)∈A が唯一つ存在する．この写像 G: B→A は FG = id_B を満たす．

定理10 次の命題は(ZF上)同値．

選択公理
A を集合，B⊂A を部分集合，f: A→B を全射とするとき，任意の写像 g: A→B に対してある写像 h: A→A が存在して g = fh となる．
A を集合，B⊂A を部分集合，f: A→B を全射とするとき，任意の全射 g: A→B に対してある写像 h: A→A が存在して g = fh となる．
A を集合，B⊂A を部分集合，f: A→B を全射とする．写像 g: A→B が g|_B = id_B を満たすとき，ある写像 h: A→A が存在して g = fh となる．

証明 (1 ⇒ 2) 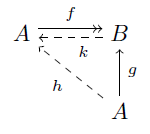定理8の3を f に適用して，fk = id_B となる写像 k: B→A を得る．そこで h := kg と置けば fh = fkg =id_Bg = g である．

2⇒3 と 3⇒4 は明らか．

(4 ⇒ 1) ${X_λ}_{λ∈Λ}$ を互いに素な非空集合の族とする． $X:=∪_{λ∈Λ}X_λ$ とする．X∩Λ= ∅ としてよい．XにもΛにも含まれない元 ∞ ∉ X∪Λ を一つ取る．A := X∪Λ∪{∞}, B := Λ∪{∞} として全射 f: A→Bを

a∈X_λ のとき　f(a) := λ
a∈Λ のとき　f(a) := ∞
a=∞ のとき　f(a) := ∞

と定める．写像 g: A→B を

a∈X_λ のとき　g(a) := ∞
a∈Λ のとき　g(a) := a
a=∞ のとき　g(a) := ∞

とする．仮定により，ある写像 h: A→A が存在して g = fh となる．このときλ∈Λに対して λ = g(λ) = f(h(λ)) だから，f の定義により h(λ)∈X_λ である．故に h|_Λ は ${X_λ}_{λ∈Λ}$ の選択関数である．

Linuxmetel | 2021年8月 5日 03:05

定理 4 の K := I∪K は K := I∪J の間違いだったりしませんか?

集合に関する命題

コメント

コメントする