線型空間の基底の存在
定理1 選択公理⇔任意の線型空間に基底が存在する.
証明(⇒) Vを任意な線型空間とする.A := { X⊂V | Xは一次独立 }とする.一次独立の定義から,A は明らかに有限性を持つ.
Aが有限性を持つとは「X∈A⇔任意の有限部分集合Y⊂ Xに対しY∈A」が成立すること.
よってTukeyの補題により A は極大元Bを持つ.
Tukeyの補題とは「有限性を持つ集合は(⊂についての)極大元を持つ」という選択公理と同値な命題のこと.Zornの補題・極大原理を参照.
B が V を生成しないと仮定する.すると B の元の一次結合で表せないような元 v∈V が存在するが,この時 B ⊊ B∪{v}∈A となり,B の極大性に矛盾する.よって B は V を生成する,即ち V の基底である.
(←) 選択公理と同値なAMCを示す.
AMC (= the Axiom of Multiple Choice)とは次の命題のこと.
非空集合の族![]() に対し,有限集合の族
に対し,有限集合の族![]() で
で
任意のλ∈Λに対して![]() となるものが存在する.
となるものが存在する.
同値性の証明はthe Axiom of Multiple Choiceを参照.
![]() を空でない集合の族とする.
を空でない集合の族とする.![]() (λ≠μ)としてよい.kを体とし,
(λ≠μ)としてよい.kを体とし,![]() を不定元の集合とみなして体 k(X) を考える.
を不定元の集合とみなして体 k(X) を考える.
単項式![]() に対し,
に対し,![]() と置き,
と置き,![]() をλ次数と呼ぶことにする.各項のλ次数が m の多項式をm次のλ斉次多項式と呼ぶことにし,その次数もλ-deg で表すことにする.f∈k(X) が
をλ次数と呼ぶことにする.各項のλ次数が m の多項式をm次のλ斉次多項式と呼ぶことにし,その次数もλ-deg で表すことにする.f∈k(X) が
f = g/h (g, hはλ斉次多項式,λ-deg(g) = λ-deg(h)+d )
と表せるとき,f をd次のλ斉次式と呼ぶことにする.
K := { f∈k(X) | 任意のλ∈Λに対し f は0次のλ斉次式 } は k(X) の部分体.よって k(X) はK上の線型空間とみなせる.V := <X> を X でK上生成される k(X) の部分空間とする.仮定より V はK上の基底をもつ.それを B と書く.
さて,λ∈Λとする.![]() の任意の元 x は
の任意の元 x は
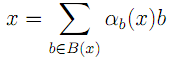
(B(x)⊂Bは有限集合,![]() )
)
と一意に表される.他の元![]() も同様に
も同様に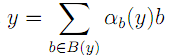 と書くと
と書くと
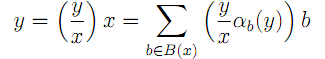
となる.表現の一意性から
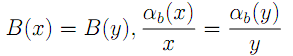
である.即ち,B(x)と![]() はxによらずにλから定まる.そこで
はxによらずにλから定まる.そこで![]() と書く.
と書く.
![]() だから
だから![]() は-1次のλ斉次式である.よって,
は-1次のλ斉次式である.よって,![]() を既約分数で表す事にすると,分母には必ず
を既約分数で表す事にすると,分母には必ず![]() の元が現れる.故に
の元が現れる.故に
![]()
と置けば各![]() は空でない有限部分集合である.よって the Axiom of Multiple Choice が成立する.
は空でない有限部分集合である.よって the Axiom of Multiple Choice が成立する.
AMC⇒選択公理 は基礎の公理を使っているから,この ⇐ の証明も基礎の公理を使っていることになる.この証明が基礎の公理無しでできるかどうかは未解決問題である.一方,次の定理の同値は基礎の公理なしで成り立つ.
定理 選択公理 ⇔ 任意の線型空間は整列可能な基底を持つ.
証明 ( ⇒ )明らか.
( ⇐ )整列可能定理を示す. X を任意の集合として, X で生成される F2 上の線型空間 F2(X) を考える.仮定より, F2(X) は整列可能な基底 B⊂F2(X) を持つ.即ち F2(X) ≅ F2(B) である. B が整列可能だから,|B| = |Pfin(B)| = |F2(B)| となり, F2(B) も整列可能であることが分かる.故に X⊂F2(B) も整列可能である.
定理2次の命題は(ZF上)同値.
- 選択公理
- 線型空間の生成系は基底を含む.
- Q-線型空間の生成系は基底を含む.
- F2-線型空間の生成系は基底を含む.
証明(1 ⇒ 2) 定理1と同様.
(2 ⇒ 3) 明らか.
(3 ⇒ 1) AMCを示す.
AMC⇒選択公理 は基礎の公理を使っているから,この 3⇒1 の証明も基礎の公理を使っていることになる.実は,3⇒1 の証明には基礎の公理は必要ない.何故ならば,仮定3から「有限集合の族についての選択公理」が導かれるからである.それをここで示しておく.
「有限集合の族についての選択公理」を示すには次の命題を示せばよい.
有限集合の族![]() が「任意のλ∈Λ に対し|Xλ|≧2」を満たすとき,
が「任意のλ∈Λ に対し|Xλ|≧2」を満たすとき,
ある族{Fλ}λ∈Λが存在して任意のλ∈Λ に対して∅≠ Fλ⊊ Xλとなる.
the Axiom of Multiple Choiceの定理2と同様である.
有限集合の族![]() が「任意のλ∈Λに対し|Xλ|≧2」を満たすとする.これらは互いに素であるとしてよい.λ∈Λとする.
が「任意のλ∈Λに対し|Xλ|≧2」を満たすとする.これらは互いに素であるとしてよい.λ∈Λとする.
Vλ := { Σx∈Xλ αxx | αx∈Q, Σx∈Xλ αx=0 }
とする.VλはQ上の線型空間で,明らかに dimQ Vλ = |Xλ|-1 である.
有限次元線型空間では,選択公理無しに次元が一意に定まることに注意する.
V := ⊕λ∈Λ Vλと置く. Gλ := { x-y∈Vλ | x, y∈Xλ, x≠y }, G := ∪λ∈Λ Gλ とすれば G は V を生成する.故に仮定から V の基底 B⊂G が存在する. Bλ := B∩Gλと置く. Gλ の定義から,Bλ は |Xλ|-1 個の x-y からなる. そこには Xλ の元が 2(|Xλ|-1) 回現れる.
(i) |Xλ|≧3 のとき.
このときは |Xλ| が 2(|Xλ|-1) を割らないから,全ての x∈Xλが同じ回数表れるということは無い.そこで mλ := min{ xが現れた回数 | x∈Xλ } として Fλ := { x∈Xλ | xが現れた回数=mλ } と置けばよい.
(ii) |Xλ|=2 のとき.
このときは |Bλ|=1 である.Bλ={b} とする.今Qは標数0だから1≠-1.そこで Fλ := { x∈Xλ | bに現れるxの係数=1 } と置けばよい.
AMCを示す為に,![]() を非空集合の族とする.各Xλは3つ以上元を持つとしても一般性を失わない.各λ∈Λに対しQ-線型空間Vλを
を非空集合の族とする.各Xλは3つ以上元を持つとしても一般性を失わない.各λ∈Λに対しQ-線型空間Vλを
Vλ := { f: Xλ→Q | ある有限集合 F⊂Xλがあって f は Xλ\F 上定数関数 }
と定義する.Gλ := { f∈Vλ | fは定数関数ではないが一点を除くと定数関数 } と置けばGλはVλを生成する.
V := ⊕λ∈Λ Vλとする.標準的な埋め込み iλ: Vλ→V が存在する.G := ∪λ∈Λ iλ(Gλ)と置けば G は V を生成する.そこで仮定より V の基底 B⊂G が存在する.Bλ := { x∈Vλ | iλ(x)∈G } とすれば Bλ⊂GλがVλの基底である.
定数関数 1∈Vλを基底 Bλの元 bi の一次結合で表す: 1=α1b1+…+αnbn.bi∈Gλで,Xλは3つ以上の元を持つから,bi: Xλ→Q が Xλ\{xi} 上定数関数になるような xi が唯一つ存在する.そこで Fλ := { x1, …, xn } とすればよい.
(2 ⇒ 4) 明らか.
(4 ⇒ 1)
![]() を互いに素な非空集合の族とする.
各Xλは無限集合としても一般性を失わない.λ∈Λとする.
Vλ := { f: Xλ→F2 | 有限個のx∈Xλを除いてfは定数関数 }⊂F2Xλ と置く.
VλはF2-線型空間F2Xλの部分空間である.x∈Xλに対して fx, gx∈Vλを
を互いに素な非空集合の族とする.
各Xλは無限集合としても一般性を失わない.λ∈Λとする.
Vλ := { f: Xλ→F2 | 有限個のx∈Xλを除いてfは定数関数 }⊂F2Xλ と置く.
VλはF2-線型空間F2Xλの部分空間である.x∈Xλに対して fx, gx∈Vλを
fx(x) := 1, y≠xのとき fx(y) := 0
gx(x) := 0, y≠xのとき gx(y) := 1
で定める.V := ⊕λ∈Λ Vλ とする. G := ∪λ∈Λ∪x∈Xλ{ fx, gx } は V の生成系である.故に仮定4から V の基底 B⊂G が存在する.
λ∈Λを取る.fxλ∈B かつ gxλ∈B となるような xλ∈Xλ が一意に存在する.
1λ∈Vλを 任意の x∈Xλ に対して 1λ(x) := 1 で定める. B が V の基底だから e(0), …, e(nλ)∈B が一意に存在して 1λ = e(0)+…+e(nλ)と書ける. e(i)∈V のVλ成分を e(i)λ と書く.
I := { 0≦i≦nλ | e(i)λは無限個の x∈Xλ に対して1を取る }
と置く.
| I | が偶数だとすると Σi∈I e(i)λは有限個の x∈Xλ を除いて 0 を取る. 故に 1λ∈Vλ は有限個の x∈Xλ を除いて 0 を取る. 今 1λ は x∈Xλ に対して 1 を取るから,Xλは有限集合で無ければならず,矛盾する.従って | I | は奇数である.
このときΣi∈Ie(i)λは有限個のx∈Xλを除いて1を取る. Yλ := { x∈Xλ | Σi∈Ie(i)λ(x)=0 } と置く. xλ∈Yλを一つ取る.今,| I | は奇数だったから, ある j∈I が存在して e(j)λ(xλ)=0 となる. j=0 としてよい.このとき,G の定義から明らかに e(0)λ=gxλである.故に n=1 かつ e(1)λ = fxλ となることが分かる. 即ち fxλ∈B かつgxλ∈B である. このとき 1λ = fxλ+gxλ だから,表現の一意性により, このような xλ は唯一つしか存在しない.
このxλを使って f: Λ→![]() をf(λ) := xλ と定めれば,f が選択関数である.
をf(λ) := xλ と定めれば,f が選択関数である.
2⇒1 の証明については,簡明な証明が知られています.かがみさんの日記の線型空間の基底の存在と選択公理 (簡単な場合)を参照.
Bases, spanning sets, and the axiom of choiceによれば「ある体Fが存在して,F-線型空間の生成系は基底を含む.」が選択公理と同値になるようです.
定義
V を集合,![]() を P(V) 上の二項関係とする.小文字 x, y は V の元を動き,大文字 X, Y, Z は V の部分集合を動くとする.次の条件を満たすとき,(V,
を P(V) 上の二項関係とする.小文字 x, y は V の元を動き,大文字 X, Y, Z は V の部分集合を動くとする.次の条件を満たすとき,(V, ![]() )を一般化線型空間と呼ぶことにする.
)を一般化線型空間と呼ぶことにする.
- Y⊂X ならば Y
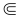 X.
X. - 「任意のλ∈Λに対してXλ
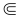 Y」ならば
Y」ならば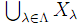
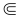 Y.
Y. - X
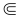 Y かつ Y
Y かつ Y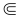 Z ならば X
Z ならば X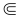 Z.
Z. - {x}
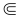 X∪{y} かつ {x}
X∪{y} かつ {x}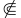 X ならば {y}
X ならば {y}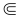 X∪{x}.
X∪{x}. - {x}
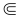 X ならば,ある有限部分集合 Y⊂X が存在して {x}
X ならば,ある有限部分集合 Y⊂X が存在して {x}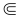 Y.
Y.
定義(V, ![]() )を一般化線型空間とする.
)を一般化線型空間とする.
- X⊂Vが独立 ⇔ {x}
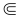 X\{x} となる x∈X は存在しない.
X\{x} となる x∈X は存在しない. - B⊂Vが基底 ⇔ B が独立でありかつ V
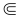 B.
B.
定理選択公理 ⇔ 任意の一般化線型空間に基底が存在する.
証明(⇒) Vを一般化線型空間とする.A := { X⊂V | Xは独立 } は有限性を持つ.
X が独立であるとする.有限部分集合 Y⊂X が独立でないと仮定する.
ある y∈Y が存在して{y}![]() Y\{y}となる.Y\{y}⊂X\{y} だから一般化線型空間の定義の1により Y\{y}
Y\{y}となる.Y\{y}⊂X\{y} だから一般化線型空間の定義の1により Y\{y}![]() X\{y} である.故に定義の3から {y}
X\{y} である.故に定義の3から {y}![]() X\{y}となり,X が独立であることに矛盾する.故に任意の有限部分集合 Y⊂X は独立である.
X\{y}となり,X が独立であることに矛盾する.故に任意の有限部分集合 Y⊂X は独立である.
逆に,任意の有限部分集合 Y⊂X が独立であるとする.X が独立でないと仮定する.ある x∈X が存在して {x}![]() X\{x} となる.このとき定義の5から,ある有限部分集合 Z⊂X\{x} が存在して{x}
X\{x} となる.このとき定義の5から,ある有限部分集合 Z⊂X\{x} が存在して{x}![]() Z である.このとき Y := Z∪{x} と置けば{x}
Z である.このとき Y := Z∪{x} と置けば{x}![]() Y\{x} となり,有限部分集合 Y⊂X が独立であることに矛盾する.故に X は独立である.
Y\{x} となり,有限部分集合 Y⊂X が独立であることに矛盾する.故に X は独立である.
従ってTukeyの補題により A は⊂に関する極大元 B∈A を持つ.B が基底でないとする.B は独立だから,V![]() Bである.V = ∪x∈V{x} だから,一般化線型空間の定義の2によりある x∈V が存在して {x}
Bである.V = ∪x∈V{x} だから,一般化線型空間の定義の2によりある x∈V が存在して {x}![]() B となる.C := B∪{x} と置けば C は独立である.
B となる.C := B∪{x} と置けば C は独立である.
C が独立でないと仮定するとある y∈C が存在して {y}![]() C\{y} である.{x}
C\{y} である.{x}![]() B だから y≠x,よって y∈B である.B は独立だから {y}
B だから y≠x,よって y∈B である.B は独立だから {y}![]() B\{y} となる.{y}
B\{y} となる.{y}![]() C\{y} = (B\{y})∪{x} だから定義の4により {x}
C\{y} = (B\{y})∪{x} だから定義の4により {x}![]() (B\{y})∪{y} = B となり矛盾する.
(B\{y})∪{y} = B となり矛盾する.
故にBの極大性に矛盾する.従ってBは基底である.
(←)
![]() を互いに素な非空集合の族とする.
V:=
を互いに素な非空集合の族とする.
V:=![]() として
として![]() を
を
X![]() Y ⇔ 任意のλ∈Λに対して「X∩Xλ≠ ∅ ならばY∩Xλ≠ ∅ 」
Y ⇔ 任意のλ∈Λに対して「X∩Xλ≠ ∅ ならばY∩Xλ≠ ∅ 」
と定める.(V, ![]() )は一般化線型空間である.
)は一般化線型空間である.
一般化線型空間の定義1から5を確かめる. 1,2,3は明らかである.
4について.{x}![]() X∪{y} かつ {x}
X∪{y} かつ {x}![]() X とする.x∈V だから,あるλ∈Λが一意に存在して x∈Xλ である.即ち {x}∩Xλ≠ ∅ である.任意のμ≠λに対して {x}∩Xμ= ∅ だから,{x}
X とする.x∈V だから,あるλ∈Λが一意に存在して x∈Xλ である.即ち {x}∩Xλ≠ ∅ である.任意のμ≠λに対して {x}∩Xμ= ∅ だから,{x}![]() X となるためには X∩Xλ= ∅ でなければならない.一方,{x}
X となるためには X∩Xλ= ∅ でなければならない.一方,{x}![]() X∪{y} の定義と {x}∩ Xλ≠ ∅ から(X∪{y})∩Xλ≠ ∅ である.故に y∈Xλ となる.従って {y}
X∪{y} の定義と {x}∩ Xλ≠ ∅ から(X∪{y})∩Xλ≠ ∅ である.故に y∈Xλ となる.従って {y}![]() X∪{x} が分かる.
X∪{x} が分かる.
5について.{x}![]() X とする.x∈V だから,あるλ∈Λが一意に存在して x∈ Xλ である.y∈X∩Xλ を一つ取る.このとき Y := {y} とすれば明らかに {x}
X とする.x∈V だから,あるλ∈Λが一意に存在して x∈ Xλ である.y∈X∩Xλ を一つ取る.このとき Y := {y} とすれば明らかに {x}![]() Y となる.
Y となる.
よって仮定により V の基底 B が存在する.V![]() B だから,任意のλ∈Λに対して B∩Xλ≠ ∅ である.x, y∈B∩Xλ とする.基底 B は独立だから {x}
B だから,任意のλ∈Λに対して B∩Xλ≠ ∅ である.x, y∈B∩Xλ とする.基底 B は独立だから {x}![]() B\{x} である.{x}∩Xλ≠ ∅,任意のμ≠λに対して {x}∩Xμ= ∅ だから,{x}
B\{x} である.{x}∩Xλ≠ ∅,任意のμ≠λに対して {x}∩Xμ= ∅ だから,{x}![]() B\{x} となるためには (B\{x})∩Xλ= ∅ でなければならない.y∈B∩Xλ だったから x=y である.従って,|B∩ Xλ|=1 が分かった.故に B が
B\{x} となるためには (B\{x})∩Xλ= ∅ でなければならない.y∈B∩Xλ だったから x=y である.従って,|B∩ Xλ|=1 が分かった.故に B が![]() の選択集合である.
の選択集合である.
参考文献
- A. Blass, Existence of bases implies the Axiom of Choice, Comtemporary Mathematics 31 (1984), 31-33, http://www.math.lsa.umich.edu/~ablass/set.html
- M. Bleicher, Some theorems on Vector Spaces and the Axiom of Choice, Fund. Math. 54(1964), 95-107
- Horst Herrlich『Axiom of Choice』
コメント
壱大整域さん、初めまして。
選択公理関連の資料を、大変興味深く拝見しております。
更新されるつど、pdf をダウンロードしております。
僕の専門はホモトピー論でしたが、数学基礎論も、
独学で勉強していたことがあります。
時機を見て、貴殿のサイトから勉強しようと思っております。
ところで、このページの基底の存在についての疑問ですが、定理1の証明で、β_{b, λ} を既約分数で表すとありますが、既約分数で表す表し方は、一意に定まるのでしょうか?不定元が一つだけの多項式であれば良いのですが、不定元がいくつもある多項式の場合、有理式を既約分数 P/Q で表すときの P と Q が、一意に決まるかどうか、疑問です。
もっとも、係数体kを有理数体Qとして、
β_{b, λ} = P/Q
とあらわしたとき、P または Q に現れる不定元の全体
H(P, Q) の基数が最小になるようにすれば、H(P, Q)
はそのような P と Q の選び方によらず一意に定まり、
F_λ として、b が B_λを動くときの、そのような
H(P, Q)∩X_λ の合併と定義すれば、
僕が感じたギャップは切り抜けられますが。
以上の点について、ご回答をいただけないでしょうか?
すみません、有理数体の Q と 多項式の Q がダブっていました。有理数体の Q は、Q' とでも置き換えてください。
一応、補足しておきます。
僕の最初のコメントで、「有理数体Q」とあるところだけ、
Q は有理数全体です。そのほかの部分の記号 Q は、多項式です。
指摘ありがとうございます。
既約分数については、一意に定まるものと思っていました。
(勿論、厳密には(x-1)/(x-2)=(1-x)/(2-x)のように一意ではありませんが、現在の議論には関係ありません。)
本当に一意か? と聞かれると自信がないのですが、とりあえずwikipedia( http://en.wikipedia.org/wiki/Irreducible_fraction )には
"The irreducible fraction for a given element is unique up to multiplication of denominator and numerator by the same invertible element."
との記述があります。
管理人様
ご回答ありがとうございます。
リンク先の記事と、更にそのリンク先を読んだところ、
確かに、既約分数表示は一意のようです。
ここで僕が問題にしているのは、定数倍を含んで一意になるかと言う意味ではないです。
体 k を係数とする多項式環が一意分解整域になるという性質が、エッセンシャルです。一意分解性域の分数体に於いては、既約分数表示が、「可逆元による定数倍を除いて」一意に決まるようですね。
以下のリンクも参考にしました:
http://en.wikipedia.org/wiki/Unique_factorization_domain#Examples
次の記述があります。
If R is a UFD, then so is R[X], the ring of polynomials with coefficients in R. Unless R is a field, R[X] is not a principal ideal domain. By iteration, a polynomial ring in any number of variables over any UFD (and in particular over a field) is a UFD.
ここで、UFD とは、一意分解整域のことです。
ありがとうございました。