定理1 Xは ￢∅∈X なる集合を表すとし，λは基数を表すとする．MC(X, λ)で命題

X上の写像fが存在して，任意のx∈Xに対し f(x)⊂x, 0< |f(x)| <λ を満たす

を表すことにする．mを2以上の整数とするとき，次の命題は(ZF上)同値．

1. 選択公理
2(m). 任意の X に対し MC(X, m)
3. ある m≧2 が存在して任意の X に対し MC(X, m)
4. 任意の X に対しある m≧2 が存在して MC(X, m)
5. 任意の X に対し MC(X, )　(the Axiom of Multiple Choice)

証明 1⇔2(2) と 2(m)⇒3 と 3⇒4 と4⇒5は明らか．m≦nに対し 2(m)⇒2(n) も明らか．なので 5⇒1 を示せばよい．その為に，選択公理と同値な命題「任意の順序集合(x, ≦)は極大反鎖を持つ」を示す．

y⊂(x, ≦)が反鎖 ⇔ yの任意の異なる2元が比較不可能
証明はZornの補題・極大原理の定理1を参照．

(X, ≦)を順序集合とする．P := P(X)＼{∅}，Q := { Y∈P | Yは有限集合 } と置く．P に仮定を適用して f: P→Q を得る．Y∈P に対し f(Y)⊂Y である．g(Y) := { a∈f(Y) | aは(f(Y), ≦)の極小元 } と置けば，各 g(Y)⊂X は反鎖で，∅ ≠g(Y)⊂Y である．反鎖 K に対し Y(K) := { x∈X＼K | K∪{x}は反鎖 } と定義する．

Xが極大反鎖を持たないと仮定すると，各 Y(K) は空でない．￢≦|P(X)|となる最小のアレフを取る．写像 h: →P(X)を

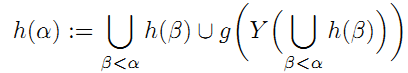
と定義すると，これは単射になるので矛盾する．故にXは極大反鎖を持つ．

「AMC(=the Axiom of Multiple Choice)⇒AC(=選択公理)」の証明に使われている命題を追っていくと，AMC⇒ACのこの証明には基礎の公理が使われていることが分かる．実は基礎の公理を仮定しない場合，AMC⇒ACは証明できないことが知られている．一方，定理における4⇒1は基礎の公理無しで証明することができるので，その証明を書いておく．

証明 選択公理と同値な次の命題を示す．

任意の集合 X に対しある正整数 m が存在して
ある順序数αとα上の関数fが存在して ∀β<α(|f(β)|≦m) かつ X=∪_β<α f(β)

整列可能定理についての定理5の条件4のこと．証明は整列可能定理についての一番最後を参照．

Xを任意の集合として P₀(X) := P(X)＼{∅} と置く． 仮定(定理の条件4)によりある正整数mとある関数 g: P₀(X)→P(X) が存在して 任意の Y∈P₀(X) に対し g(Y)⊂Y, 0 < |g(Y)| < m+1 を満たす． ￢U⊂X となる集合 U を一つ取り，g(∅) := Uと定義しておく． アレフで，￢≦ |P(X)| となるものが存在するので，その様なのうち最小のものを取る． 順序数α<に対し

G(α) := g(X＼∪_β<α G(β))

で写像 G: →P(X)∪{U} を定める． 明らかに，G(α)=G(β)≠U ならばα=βである． G(α)=U となるαが存在しないと仮定すると， G: →P(X) は単射となる． しかしこれは￢≦ |P(X)| に矛盾する． 従って G(α)=U となる順序数αが存在するので， そのようなαのうち最小のものを取る． このとき f := G|_α とする． U = G(α) = g(X＼∪_β<α G(β)) だから， ∪_β<α G(β)=X である． またβ < αに対し f(β) = G(β) = g(X＼∪_γ<β G(γ)) だから g の性質より |f(β)| ≦ mが分かる． よってこの f が条件を満たす．

定理2 選択公理
⇔集合 X が「任意の x∈X に対し |x|≧2 」を満たすとするとき， X 上の写像 f が存在して，任意の x∈X に対し f(x) ⊊ x, 0<|f(x)|<∞ を満たす．

証明 (⇒)明らか．

(←) を互いに素な非空集合の族とする． P := {A⊂ | |A|≧2 } として P に仮定を適用し写像 f を得る． |A|=1 となるような A⊂に対しては f(A) := A として f の定義を拡張しておく． S := ∪_λ∈Λ∩_n∈N fⁿ(X_λ)と置く． (但し fⁿ は f のn回合成である．) このときSがの選択集合である．

定理3次の命題は(ZF上)同値．

1. 選択公理
2. 集合 X が「任意の x∈X に対し x≠ ∅ 」を満たすとするとき， X 上の写像 f が存在して「任意の x∈X に対し ∅ ≠ f(x)⊂x, |f(x)| は奇数」を満たす．
3. 集合 X が「任意の x∈X に対し |x|≧2 」を満たすとするとき， X 上の写像 f が存在して「任意の x∈X に対し ∅ ≠ f(x)⊂x, |f(x)| は偶数」を満たす．

証明AMC ⇒選択公理により明らか．

定理3の条件2をOAC(=Odd Axiom of Choice)，条件3をEAC(=Even Axiom of Choice)という． この証明は勿論基礎の公理が使われているが，実は基礎の公理無しで次のことが言える．

定理選択公理 ⇔ OACかつEAC

証明定理2を使う． 集合 X が「任意の x∈X に対し |x|≧2 」を満たすとする． X にEACを適用して写像 g を得る． 集合 { g(x) | x∈X }にOACを適用して写像 h を得る． このとき x∈X に対して f(x) := h(g(x)) と置けば 写像 f は「任意の x∈X に対し ∅ ≠f(x) ⊊ x, |f(x)|<∞」を満たす．