∪∩の分配法則
集合の共通部分や和集合を取る演算は分配法則 x∩(y∪z) = (x∩y)∪(x∩z),x∪(y∩z) = (x∪y)∩(x∪z) が成り立つことが良く知られているが,これを無限個に拡張すると選択公理と同値になる.
定理
![]() は非空集合の族を表すとし,X :=
は非空集合の族を表すとし,X :=![]() と置く.
次の命題は同値.
と置く.
次の命題は同値.
- 選択公理
任意の
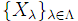 と,
定義域が∪λ∈Λ({λ}×Xλ)である写像Aに対し
と,
定義域が∪λ∈Λ({λ}×Xλ)である写像Aに対し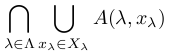 =
=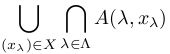
任意の
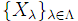 に対し
に対し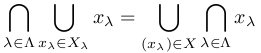
証明 (1⇒2) まず⊃は選択公理によらずZFで成立している.
任意のu∈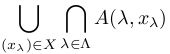 を取る.
即ち,ある元 (yλ)λ∈Λ ∈X が存在して
u∈∩λ∈Λ A(λ, yλ) となる.
よって各λ∈Λに対して
u∈A(λ, yλ)⊂
を取る.
即ち,ある元 (yλ)λ∈Λ ∈X が存在して
u∈∩λ∈Λ A(λ, yλ) となる.
よって各λ∈Λに対して
u∈A(λ, yλ)⊂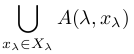 だからu∈
だからu∈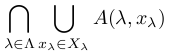 である.
である.
なので⊂を示せばよい.u∈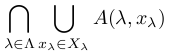 とする.
即ち,任意のλ∈Λに対してu∈
とする.
即ち,任意のλ∈Λに対してu∈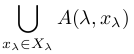 である.
つまりBλ := { xλ∈ Xλ | u∈A(λ, xλ) }は空でない.
そこで{Bλ }λ∈Λ に選択公理を適用して
元(yλ )λ∈Λ∈Πλ∈Λ Bλ⊂X を得る.
このとき
である.
つまりBλ := { xλ∈ Xλ | u∈A(λ, xλ) }は空でない.
そこで{Bλ }λ∈Λ に選択公理を適用して
元(yλ )λ∈Λ∈Πλ∈Λ Bλ⊂X を得る.
このとき
u∈∩λ∈Λ A(λ, yλ)
⊂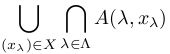 .
.
(2⇒3) A(λ, x) := x として仮定を適用すれば明らか.
(3⇒1) 集合uを任意に一つ選んでおく.
任意の![]() を取り,
λ∈Λに対して Yλ := { {u, x} | x∈Xλ } と置く.
Y := Πλ∈Λ Yλとして
{Yλ }λ∈Λ に仮定3を適用すれば
を取り,
λ∈Λに対して Yλ := { {u, x} | x∈Xλ } と置く.
Y := Πλ∈Λ Yλとして
{Yλ }λ∈Λ に仮定3を適用すれば
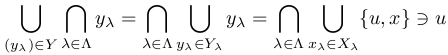
従って,ある(yλ)∈Yが存在して u∈∩λ∈Λ yλ となることが分かる.Yλの定義から yλ = {u, xλ} となるxλ∈Xλが唯一つ存在する. このとき (xλ)λ∈Λ ∈X だから X ≠ ∅ .
コメント
①「{X_λ}_{λ∈Λ}は非空集合の族を表すとし」の仮定は2.と3.に不要。
②∪_{x_λ∈X_λ}A(λ,x_λ)は∪_{x∈X_λ}A(λ,x)など、等号の左辺側のx_λの添え字λはなしと思います。