順序数・濃度の簡単なまとめ
このページでは選択公理を仮定しない．
順序数についてはそのうち書きます． |X| で X の濃度を表す．
定義 X と Y を集合とする．
- |X|≦|Y| ⇔ 単射 X→Y が存在する
- |X|=|Y| ⇔ 全単射 X→Y が存在する
- |X| < |Y| ⇔ |X|≦|Y| かつ |X|≠|Y|
- |X|≦*|Y| ⇔ 全射 Y→X が存在するか， X= ∅
- |X| <* |Y| ⇔ |X|≦* |Y| かつ |X|≠|Y|
命題1
- |X|≦|Y| かつ |Y|≦|X| ならば |X|=|Y| (Bernsteinの定理)
- |X| < |P(X)| (Cantorの定理)
- |X|≦|Y| ならば |X|≦*|Y|
- |X|≦*|Y| ならば |X|≦|P(Y)|
定義 κ と λ を濃度とする． κ=|X|, λ=|Y|, X∩Y= ∅ となるような X, Y を取る．
- κ+λ:=|X∪Y|
- κ・λ:=|X×Y|
- κλ :=|XY| (XY:= { f: Y→X } )
- κ=λ+μ となる濃度 μ が唯一つ存在するとき， κ-λ:=μ
- κ=λ・μ となる濃度 μ が唯一つ存在するとき， κ÷λ:=μ
もちろんこれらはwell-definedである．
定義
整列された無限集合 X を使って |X| と表される濃度をアレフと言い， 
で表す．特に，自然数全体がなす整列集合で表されるアレフを 0 と書く．
命題2 二元集合 2= { 0, 1 } の濃度を 2 と表せば，任意の濃度 κ に対して 2・κ=κ+κ, κ2=κ・κ である．また κ=| X | のとき 2κ=| P(X) | ．
命題3
任意の濃度 κ, λ について
κ≦λ ⇔ ある濃度 μ が存在して κ+μ= λ
命題4 濃度 κ, λ≧2 に対し κ+λ≦κ・λ ．
証明 κ=|X|, λ=|Y|, X∩Y= ∅ となる集合を取る． a≠b となる a, b∈X ， s≠t となる s, t∈Y を取る． φ: X∪Y→X×Y を
φ(x) := <x, s> (x∈X のとき)
φ(x) := <a, x> (x∈Y＼{ s } のとき)
φ(x) := <b, t> (x=s のとき) .
と定めれば φ は単射である．
命題5
任意のアレフ に対して2= ．
証明 無限順序数 α に対し |α×α| = |α| を示せばよい． 任意の順序数 β>0 は
β = ωβ1・m1+…+ωβn・mn, 1≦n, m1, …, mn < ω, β≧β1 > … > βn
の形に一意に書ける(Cantor標準形．キューネン第I章演習問題6の解答を参照)． 全単射 g: ω×ω→ω を g(0, 0)=0 となるように一つ取る． β, β'<α が与えられたとき α≧β1 > … > βn を使って
β = ωβ1・m1+…+ωβn・mn
β' = ωβ1・m1'+…+ωβn・mn'
と書いて f(β, β') := ωβ1・g(m1, m1')+…+ωβn・g(mn, mn') と定めれば，これは全単射 f: α×α→α を与える．
命題6
任意のアレフ, 'に対し・'=+'=max{ , ' } ．
証明
'≦ としても一般性を失わない．このとき
命題7
濃度 κ, λ, μ とアレフ が κ・≦λ+μ を満たすとき， κ≦μ または ≦λ である．
証明
κ=|X|, λ=|Y|, μ=|Z| となる集合 X, Y, Z と =|W| となる整列順序集合 W を取る．
Y∩Z = ∅ としてよい．
仮定より単射 f: X×W→Y∪Z が存在する．
A := f-1(Y), B := f-1(Z) とすれば |A|=|Y|=λ, |B|=|Z|=μ, X×W=A∪B である．
(i) {x}×W⊂A となる x∈X が存在するとき．
=|W| = |{x}×W|≦|A|=λ である．
(ii)どの x∈X についても ￢{x}×W⊂A となるとき．
wx := min{ w∈W | <x, w>∈B } と書けば κ= |X| = |{ <x, wx> | x∈X }|≦|B|=μ である．
命題8
濃度 κ, λ, μ とアレフ が κ・λ≦+μ を満たすとき， κ≦ または λ≦μ である．
証明
κ=|X|, λ=|Y|, μ=|Z| となる集合 X, Y, Z と =|W| となる整列順序集合 W を取る．仮定より単射 f: X×Y→W∪Z が存在する．
(i) ある x∈X について f({x}×Y)⊂Z となるとき．
g: Y→Z を g(y) := f(x, y) で定めれば g は単射で λ=|Y|≦|Z|=μ である．
(ii)任意の x∈X について ￢f({x}×Y)⊂Z となるとき．
Yx := { y∈Y | f(x, y)∈W } ≠ ∅ である． g: X→W を g(x) := min{ f(x, y) | y∈Yx } で定めれば g は単射で κ=|X|≦|W|= である．
命題10
濃度 κ, λ とアレフ が ≦κ・λ を満たすとき， ≦κ または ≦λ である．
証明
κ=|X|, λ=|Y| となる集合 X, Y と =|W| となる整列順序集合 W を取る．単射 f: W→X×Y が存在する． πX, πY をそれぞれ X×Y から X, Y への射影として U := πX(f(W))⊂X, V := πY(f(W))⊂Y と置く．
W の整列順序を使って， U, V は整列可能である．また f(W)⊂U×V である．
このとき命題6を使って
= |W|≦|U×V| = |U|・|V| = max{ |U|, |V| }
となる．
故に ≦|U| または ≦|V| であるが，それぞれ ≦κ, ≦λ を導く．
命題11
Pfin(X) := { Y⊂X | Y は有限集合 } と置く．
整列可能な無限集合 X に対し |X| = | Pfin(X) |
証明 X の整列順序 ≦ を取る．
Y∈Pfin(X) を取り， |Y| = n とする．このとき順序同型 fY: n→(Y, ≦) が一意に存在する．そこで f(Y) := <n, fY(0), …, fY(n-1)> ∈ {n}×Xn と定める．これにより単射 f: Pfin(X)→∪n=0∞({n}×Xn) が定義できる．
次に，命題5により単射 g2: X2→X が存在する．そこで n > 2 に対して gn: Xn→X を
gn(x1, …, xn-1, xn) := g2(gn-1(x1, …, xn-1), xn)
で定めると，各 gn は単射である． g0: X0→X を一つ取り， g1 := idX とする．この { gn }n=0∞ より単射 g: ∪n=0∞({n}×Xn)→∪n=0∞({n}×X) が
g(n, x1, …, xn) := (n, gn(x1, …, xn))
で定義できる．
また，命題6により |ω×X| = |X| である．
以上により
|X|≦|Pfin(X)|≦|∪n=0∞({n}×Xn)|≦|∪n=0∞({n}×X)| = |ω×X| = |X|
である．
補題12 基数 λ, μ, κ が λ+μ=λ+κ を満たすとき，ある基数 ξ, ζ, η が存在して λ=λ+ξ=λ+ζ，μ=ξ+η，κ=ζ+η を満たす．
証明 互いに素な集合 X, Y, Z を |X|=λ，|Y|=μ，|Z|=κとなるように取る．すると |X|+|Y| = |X|+|Z| だから全単射 f: X∪Y→X∪Z が存在する．
Y0 := { y∈Y | 任意の n>0 に対して fn(y)∈X }
Y1 := Y＼Y0
X0 := ∪n > 0fn(Y0)
X1 := X＼X0
とする．このとき f|X0∪Y0: X0∪Y0→X0 は全単射である．よって ξ:=|Y0| と置けば
λ+ξ = |X|+|Y0| = |X1|+|X0|+|Y0| = |X1|+|X0| = |X| = λ
である． η := |Y1| とすれば μ= |Y| = |Y0|+|Y1| =ξ+η である．
g:=f-1 に対しても同様のことをする．即ち
Z0 := { z∈Z | 任意の n>0 に対して fn(z)∈X }
Z1 := Z＼Z0
としてζ := |Z0|，η' := |Z1| とすれば λ+ζ=λ，κ=ζ+η'となる．後はη=η'を示せばよい．
y∈Y1 とすると，定義からある ny > 0 が一意に存在して f1(y), …, fny-1(y)∈X ， fny(y)∈Z が成り立つ．このとき gny(fny(y))∈Y だから fny(y)∈Z1 である．よって写像 Y1→Z1 が Y1∋y |→ fny(y)∈Z1 により定義される．これは明らかに全単射である．よって η= |Y1| = |Z1| =η' である．
補題13 濃度 κ, λ, μ が 2κ=κ+λ と κ=κ+μ を満たすとき， λ≧2μ である．
証明 κ=|X| となる X を取る．仮定より，集合 M, N⊂P(X) ， Y, Z⊂X を
P(X) = M∪N, M∩N= ∅, |M|=κ, |N|=λ,
X = Y∪Z, Y∩Z= ∅, |Y|=κ, |Z|=μ
となるように取れる． |Y|=κ=|M| だから，全単射 f: Y→M が取れる． A∈P(Z) に対して
h(A) := A∪{ y∈Y | y ∉ f(y) } ⊂ Z∪Y = X
と定義する． Y∩Z = ∅ だから， h: P(Z)→P(X) は単射である．また A∈P(Z) に対して h(A) ∉ M である．
h(A)∈M と仮定する． f: Y→M が全単射だから f(y)=h(A) となる y∈Y が取れる．このとき y ∉ A に注意すると
y∈f(y) ⇔ y∈h(A) ⇔ y ∉ f(y)
となり矛盾する．
従って h は単射 P(Z)→N を定め， λ≧2μ が分かる．
命題14
0≦κ ならば
2κ-κ=2κ である．
証明
まず 2κ+κ=2κ を示す．
明らかに 2κ+κ≧2κ だから 2κ+κ≦2κ を示せばよい．
今 0≦κ だから κ+1=κ である．
故に 2κ+κ≦2κ+2κ=2κ+1=2κ となる．
後は κ+λ=2κ ならば λ=2κ を示せばよい． まず κ+λ=κ+2κ が成り立つから，補題12によりある ξ, ζ, η が存在して κ=κ+ξ=κ+ζ，λ=ξ+η，2κ=ζ+η が成り立つ． 2κ=κ+λ かつ κ=κ+ζ に 補題13を適用すれば λ≧2ζ > ζ を得る．従って 2λ≧ζ+η=2κ=2κ+1 である．一方 2κ≧λ だったから 2κ+1≧2λ である．故に 2λ=2κ+1 を得る．従って λ=2κ である．
命題15
X を集合とする． |α|
|X| となるような順序数 α が存在する．
証明 Γ(X) := { α | α は順序数， |α|≦|X| } と置く． Γ(X) は集合である．
W:= { R⊂X×X | R は X のある部分集合を整列する } と定義する． W は集合である．よって「 W に現れる整列順序と同型な順序数全体」も集合である．この集合は Γ(X) と一致する．
順序数の推移的な集合は順序数だから， Γ(X) も順序数である．よって Γ(X) ∉ Γ(X) だから | Γ(X) || X | となる．
この Γ をHartogs関数という．
また κ=|X| のとき κ* := |Γ(X)| と書く．これをHartogs numberという．Hartogs numberはアレフである．
命題16
- Γ(X) は |α|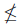|X| となるような順序数 α のうち最小の順序数である．
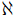
- κ* は 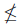κ となるようなアレフ 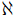のうち最小のアレフである．
- κ*≦22κ2
- κ*≦222κ
- 無限濃度 κ に対して κ**=(κ+κ*)*
- 無限濃度 κ に対して (κ2)*=κ*
証明 (3) κ=|X| となる X を取り
W:= { R⊂X×X | RはXのある部分集合を整列する }
と置く．明らかに |Γ(X)|≦*|W| である．よって |Γ(X)|≦|P(W)| であり
κ*=|Γ(X)|≦|P(W)|≦|P(P(X×X))|=22|X|2=22κ2
となる．
(4) κ=|X| となる X を取り α∈Γ(X) とする．単射 f: α→X に対して Af := { f''β | β < α } ∈P(P(X)) と定める． B := { Af | α∈Γ(X), f: α→X は単射 } と置けば B⊂P(P(X)) となる． φ: B→Γ(X) を φ(Af) := dom(f) とすれば φ は全射となる．よって |Γ(X)|≦*B だから |Γ(X)|≦P(B)≦|P(P(P(X)))| ．
(5) κ*≦κ+κ* だから κ**≦(κ+κ*)* である． κ** < (κ+κ*)* と仮定すると κ** はアレフだから， (κ+κ*)* の最小性より κ**≦κ+κ* となる．よって命題9により「 κ**≦κ または κ**≦κ* 」となり矛盾する．故に κ**=(κ+κ*)* である．
(6) κ≦κ2 だから κ*≦(κ2)* である． κ* < (κ2)* と仮定すると κ* はアレフだから (κ2)* の最小性により κ*≦κ2 となる．故に命題9から κ*≦κ となり矛盾する．故に κ*=(κ2)* である．
定義 集合 X に対して K(X) := { f: α→X |α は順序数， f は単射 } をKruse関数という． κ=|X| のとき κ† := |K(X)| と書く．
明らかに，次が成り立つ．
命題17
- κ† ≦ 2κ2
- κ† ≦ 22κ
- κ < κ†
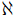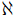- アレフ に対して †=2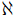
命題18
- κ†・μ† ≦ (κ+μ)†
- κ≧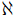0 ⇒ κ†+κ†=κ†
- κ+κ=κ ⇒ (κ†)2=κ†
命題19
κ≧0 とアレフ が κ†≦κ+ を満たすとき， κ < κ†=2κ≦ である．
証明
κ≧0 だから命題18より κ†+κ†=κ† である．よって κ+κ≦κ†+κ†=κ†≦κ+ となる．故にある '≦ が存在して κ+κ=κ+' となる．このとき '≦κ+κ だから命題9により '≦κ が分かる．故に κ+'=κ であるから κ+κ=κ となる．従って命題18より (κ†)2=κ† が従う．仮定より κ†≦κ+ だから，ある μ≦κ と ''≦ が存在して κ†=μ+'' と書ける．このとき ''≦κ† だから κ†・''≦(κ†)2=κ†≦κ+ である．命題7により κ†≦ または ''≦κ が分かる．
''≦κ と仮定すると κ†=μ+''≦κ+κ=κ となり κ < κ† (命題17)に矛盾する．従って κ†≦ である．よって κ < κ†≦ であり， κ がアレフだから κ†=2κ となる．
コメント
悩める門外漢に教えてください
（よく出会うアマチュア質問とは思いますがお願いします）：
N: 自然数
N1: 各数の先頭に”0. “をつけて得る集合。（自然数には最高桁が見える、が前提）
N2: N1の要素に”3”を無限につけて得る数のうち異なるものだけの集合。
注 Nの328と3283 はN1では0.328と0.3283 になります。N2を作る際、両数はともに0.328333333….. と0.328333333… になるので一つになります。つまりN2はNよりはるかに小さい集合になります。
命題は：N2は可算か？
自明に可算と思えます。では並べて見せてください：（中略）対角線論法で列挙されなかった数が生成できました。（それは終わり？の方は３でない数が続く特殊数です。）
それがN2に入っていたらN2はNより大きい、となるので嘘でしょう。
つまり、対角線論法が生成する数はN2に入っていません。
なぜそう言える？
私が思いつく答えらしい答えは、「自然数は有限最高桁を持つから。。。」でしょう。すると、更に疑問がわきます：ならば、Nは有限集合なのか？Nは最高桁数の上限MをパラメータとしてN(M)と表され、Mが有限のときは有限である集合なのか？Mを段々大きくして無限に持って行く可能無限集合の世界なのか？カントールのお話しは「実無限と可能無限の比較話だったのか」「無限集合（実数集合）は有限集合より大きい」と言うアホ話だったのか？
N２にあたる集合を持ってきてカントールの意義の説明は読んだことがありますが、それらは「自然数は最高桁があるから」でした。Nは有限集合と言うなら、私は更に納得できない！！！
もし、「自然数には最高桁があるが、見ることはできない」ならば、自然数を鏡像反転し、後には３を無限個つける、というアルゴリズムで定義することもできます。328 → 0.8233333….
ここら辺で何か、お助けマン公理が登場のようにも思いますが教えてください。
対角線論法で(具体的に)どうやって数を生成したのか分かりませんが、その数xはある桁から先に無限個3が並ぶ数なのですか? もしそうでないならば、N2の定義からxはN2に含まれません。
前回は、試し、とばかりスイッチを押したので名無しになりました。失礼。迷える狼
前回質問は、
1) 自然数集合Nは、最高桁Mを引数とするN(M)と表せる有限集合か？
2) 小数が、小数点M桁以降から異なるとき、両数は異なる、と言えるか？Mが有限なら当然ですが、Mは無限です。
今回の質問は「背理法の適用について」です。背理法は、YES,NO回答をもつ命題を決め、YES者とNO者を想定し、相手の矛盾を上げつらい勝者を決める方法です。今の場合「(0,1)全実数Rの全要素をNに沿って並べ得るか？」です。
知られている論は「NO者がYES者に向かって、YESと言うなら見せてください」から始まります。公平な審判は疑問を持ちます：
１．「ある」なら見せ得るものか？見せる義務はあるのか？
２．N者先攻は不公平ではないか？
３．Nはアルゴリズム定義（KがあればK+１もある）ですが、Rの方は列挙定義しかありません。これは異なる集合の比較ではないか？
です。背理法は例外なく「NOと言う方が有利」ですが、有限問題ならその差は問題ない、ことは明らかです。以下の例は以上の疑問を踏まえています。
YES者は以下のようにアルゴリズムで提示します：最初に任意の数aを挙げます。 次にこれから対角線論法（以下D論と呼ぶ）で得られるすべての数を並べます。（例えば小さい順に。）一般にｋ個まで得たら、それら全部からD法で生成される異なる数全部を並べます。このように生成される順序つき実数系列をR(a)とします。これをNO者に見せるのです。
NO者は、それでは見えないよ、と言うかもしれません。しかし、アルゴリズムはNO者が使うであろうD法を使って記述しているのです。自縄自縛です。じゃんけんで相手に「先に良く見えるように見せろ」と言えばジャイアンです。
更に言えば、我々はアルゴリズムで定義されていない集合（今の場合実数）をa, b, ……..と表記してわかったような気がします。これにD法を適用する、などと軽く言います。しかし、上に定義したR(a) では、aの後に無限個が並びます。１個でも増えるたびに無限個の数が並びます。したがって無理に書くとすれば
a …… b…. c ….. のように 無限部分「…..」が分散して現れます。このような表現数列にD法をどのように適用するのでしょうか？D法の記述では、bは何桁目、とか指定することが必要でしょう。bはすでに無限番の後です。これはつまり、NO者にはこの表現の解析能力がない、と思われます。
NO者は言うかもしれません：反論を見て作り直している。後出しでずるい。
ではYES者も、並べてみせるから実数を見せて下さい、とNO者に求める権利があります。NO者は（できないと言うその主張から）当然できません。でも並べてみよ、と言う限りその義務が発生します。問題自身を提示できない、ので戦わずしてYES者の勝ち（＝Nから実数Rへの全単射が存在する）と言えるでしょう。
これは一休の屏風の虎退治と同じ話です。虎を追い出せば退治してみせる、と言う一休は正論だ、が一般人の了解です。
長く書きましたが、内容は前回と同じルーツです：自然数集合は実数集合とは、写像などは考えてはいけない異質のものではないか。
あるいは：無限集合については、その要素のどれとも異なるものがその要素であることもある、と言う命題が成り立つ世界はどの公理にも反しない、のではないか？（既存の集合定義とには矛盾することはわかりますが。）
著者は公理系の権威とお見受けしますので教えてください。
今見ました。ありがとうございます。
その数ｘがN２に属さない理由を話題にしています。「ある桁」に言及しなければ説明できないではないかと。
自然数集合は「ある桁」が引数なのですか？そうであれば、そのことを初めから言ってもらえば、実数への全単射がない、ということはカントールを要しません。この理解困難で発生する数学嫌いは無くなるでしょう。
ç¹°ãè¿ãã§ç³ã訳ããã¾ãããä»åã®è³ªåãã¼ãã¯ãèªç¶æ°éåã ã£ã¦ã¹ãéåã ãã§ãã
æ©ããç¼ã¯ãã«ã³ãã¼ã«ã®å®çãã«çããæ±ãã¦ããã®ã§ã¯ããã¾ãããéã«ããããé©ç¨ãã¦ããªããã¨è¨ãããã®ã§ãã
対è§ç·è«æ³ããåæ¡ã§ç°ãªãæ°ãæ¡ç¨ãããã¨è¨ãããã¹ãéåãèãã¦ãããã¨ãæããã«ãªããå®çã®å³è¾ºãæ³ãã¾ãããããèªç¶æ°éåã ã£ã¦ã¹ãéåã§ãã100æ¡ã¾ã§ã®èªç¶æ°ã¯ã¹ãéå10ã®100ä¹ãã®è¦ç´ ã§ããã ãããããã«ã³ãã¼ã«å½é¡ã®å³è¾ºã§ãã左辺ã¯ãã¤ç»å ´ããã®ã§ãããï¼
ããå°ãæ¸ããªãã°ï¼å®æ°ã®å°æ°ç¹ä»¥ä¸100æ¡ã¾ã§èªç±å¤ã§ã以éã¯ãã¹ã¦3 ã¨ããå°æ°å ¨ä½ã¯ã100æ¡èªç¶æ°ï¼ã¹ãéå10ã®100ä¹ã¨åãè¦æ¨¡ã§ãããã®äºå®ããN(100)=R(100)ã¨æ¸ãã¾ããããä¸è¬ã«ã¯ãèªç¶æ°ã®Mæ¡ãå®æ°ã®å°æ°ç¹ä»¥ä¸Pæ¡ãèããã¨ãã¦ãN(M) ã¨R(P)ã大å°æ¯è¼åé¡ã«ãªãã¾ããM>Pãªãèªç¶æ°ã®æ¹ãå®æ°ããå¤ãããã¨ããçºçãã¾ãããã®æå³ã§ã®èªç¶æ°ã¨å®æ°ã¨ã®ã©ã£ã¡ãå¤ããã¯Nã¨Pã®å¤§å°ã¨åãã§ãã
ã«ã³ãã¼ã«ã«ãããèªç¶æ°ããå®æ°ãå¤ããã¨ã®è¨¼æãã¯ã«ã³ãã¼ã«ã®å½é¡ã使ã£ã¦ã¯ããªãã¦ãæé»ã®æ¡æ°ä»®å®ãM<Pãã®èªæãªå¸°çµã§ããã²ã©ãã¯ãMã¯æéã¨ããèè ããã¾ããä½æ ãããªãã¨ã許ãããï¼
正直何いってんのか分からないのですが。
＞その数ｘがN２に属さない理由を話題にしています。「ある桁」に言及しなければ説明できないではないかと。
「ある桁」に言及する必要はありません。何故ならばそんなもの存在しないからです。今証明すべきことは「その数xはある桁から先に無限個3が並ぶ数」でない、ということです。
先には文字化けに気づかず失礼しました。
考え方の説明は伝わらないものである、ですので、具体的な実数列挙アルゴリズムを提案します。どうでしょう？
嘘！に決まっている、と思わないで、どこから誤りか教えて頂きたいのですが。
提案：対角線論法で新数を生成できない実数の並べ方
任意の一つの実数をa1 とする。
例
a1=0.862848585....
対角線論法（以下D法と呼ぶ）を、k個の実数並びから一つの数を生成する規則と考える。
対角がないときにはそれ以前の数と同じ並びとする。（厳密ルールは以下の例からわかるでしょう。）それをa2とする。
a2=0.962848585....
しかし、多進数表示では、D法による生成が一意でないので、議論の簡明さのために２進表示を使います。あらためて例を作ります。
a1=0.1100100.......
これからD法で生成される数をa2として並べる。
a2=0.0100100.......
a1, a2からD法で得る数をa3とする。
a3=0.0000100.......
以下同様にa1, a2, .., ak からD法で得る数をak+1とする。
以下のような表ができる。
a1 : 0.1100100.......
a2 : 0.0100100.......
a3 : 0.0000100.......
a4 : 0.0010100.......
a5 : 0.0011100.......
a6 : 0.0011000.......
a7 : 0.0011010
::::::::
定理１：実数の並び R(a1) から対角線論法は R(a1) に属さない数は生み出せない。
理由：定義から。
定理２：R(a1)と自然数は同じ濃度である。
理由：自然数は kからk+1を一意に生成する。
R(a1)は、1からkまでからk+1を一意に生成する。
考察１：この表右辺数字部分をマトリクスと考える。
ここでは、マトリクスの(1,1)から下への対角線で考えた。しかし、任意の列
(1,k)から始めれば（たぶん）異なる数が生成される。それら全部をR(1,p)と書く。
するとD法を拡大解釈すると、R(1,1) R(1,2) R(1,3) ....を生成するとみなすこともできる。
しかしこれら全部合わせて一列に列挙して考えることができる。
考察２：R(a1)は実数の、無限集合とは言え、ほんの一部です。真部分集合であることの証明も簡単です。だからこれだけでは全部を挙げてはいない、と言えます。しかしそれは今の主旨、対角線論法はどんな並びからでも新数を列挙するは否定される、とは関係ない話です。
>>迷える素人さん
1年以上前のポストに対するレスになり申し訳ないのですが…
あなたのおっしゃるR(a1)と言うのは、a1,a2,...を並べた表のことですか？
ならば、「定理１：実数の並び R(a1) から対角線論法は R(a1) に属さない数は生み出せない。」は誤っています。
よく見ると分かるように、自然数kに対して、この表(R(a1))の中の実数akは、a1の小数第(k-1)位までの0と1を反転させて、第k位以降はa1と同じ、という実数になっています。
したがって、この表に属する任意の実数は、十分先の桁では(akなら第k位以降)、a1と同じになっています。
対角線論法で得られる数と言うのは、（私の理解が正しければ、）「すべての自然数kに対して」、小数第k位がakの小数第k位と異なる数、のことです。
この表に対角線論法を適用した場合、得られる実数は、a1の「すべての桁」を反転させた数です(この実数をbと呼ぶことにします)。
先ほど述べたように、表の中の任意の実数akは、第k位以降はa1と同じですから、bとは異なります(bは第k位もa1とことなる)。
ですから対角線論法は表に属さない数を生み出しています。
I don't fully understand Japanese, but it seems that for proposition 5 you only proved 2^κ+κ=2^κ; I believe that to prove 2^κ-κ=2^κ, you need to show that for any μ satisfying μ+κ=2^κ, we have μ=2^κ.
コメントありがとうございます。
指摘の通り、命題5の証明は間違っているので、そのうち直します。
Thank you very much for your comment.
Actually, as you pointed out, the proof of proposition 5 is completely wrong.
Now I have been trying to fix it.
I hope I'll understand the correct proof.
命題5(現在の番号は命題14)の証明を直しました。