選択公理について

定義 Xを集合とするとき，次の条件を満たす写像 f: X＼{∅} → ∪_x∈X x を集合 X の選択関数という．

任意の非空集合 x∈X に対して f(x)∈x

次の命題を選択公理と呼ぶ．

選択公理 任意の集合は選択関数を持つ．

定義全射 g: Λ→A をΛを添え字集合とする集合族という．X_λ := g(λ) と置いて，この集合族を ${X_λ}_{λ∈Λ}$ で表すことが多い．また，次の条件を満たす写像f: Λ→ $∪_{λ∈Λ}X_λ$ を集合族 ${X_λ}_{λ∈Λ}$ の選択関数という．

任意のλ∈Λに対して f(λ)∈X_λ

集合族 ${X_λ}_{λ∈Λ}$ の選択関数全体からなる集合を $Π_{λ∈Λ}X_λ$ で表す．f∈ $Π_{λ∈Λ}X_λ$ に対して x_λ := f(λ) と置くとき，f = ( x_λ )_λ∈Λ 等と表すことがある．

定理次のの命題は(ZF上)同値．

選択公理
非空集合の族 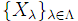${X_λ}_{λ∈Λ}$ に対して，選択関数が存在する．
互いに素な非空集合の族 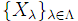${X_λ}_{λ∈Λ}$ に対して，選択関数が存在する．
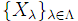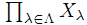非空集合の族 ${X_λ}_{λ∈Λ}$ に対して， $Π_{λ∈Λ}X_λ$ ≠∅．
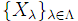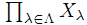互いに素な非空集合の族 ${X_λ}_{λ∈Λ}$ に対して， $Π_{λ∈Λ}X_λ$ ≠∅．
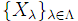${X_λ}_{λ∈Λ}$ を互いに素な非空集合の族とするとき，ある集合 C が存在して「任意のλ∈Λに対し|X_λ∩C| = 1」を満たす．この C を選択集合という．

証明(1 ⇒ 2) 集合 { X_λ | λ∈Λ } の選択関数を g とすれば f(λ) := g(X_λ) が ${X_λ}_{λ∈Λ}$ の選択関数である．

2⇒3 と 3⇒5 と 2⇒4 と 4⇒5 は明らか．

(5 ⇒ 6) ${X_λ}_{λ∈Λ}$ を互いに素な非空集合の族とする．仮定5により元 ( x_λ )_λ∈Λ ∈ $Π_{λ∈Λ}X_λ$ が取れる．このとき C := { x_λ | λ∈Λ } と置けばよい．

(6 ⇒ 1) X を集合とする．￢∅ ∈X としてよい．Y := { {x}×x }_x∈X とすればY は互いに素な集合の族であるから，選択集合 C が存在する．このとき x∈X に対して C∩({x}×x) = { <x, f(x)> } と置けば f が X の選択関数である．

manifolds | 2016年3月11日 09:28

初歩の質問です。最初の式
f: X→∪x∈X x
において、一番右にある x は、元(要素)なのでしょうか。部分集合なのでしょうか。

記号 ∪ が和集合を表しているならば、 x を部分集合として
f: X→∪x∈X { x }
とでも書くべきでは？

管理人 | 2016年3月12日 16:57

xは元です。
Xは集合の集合なので和集合の取り方はこれでよいです。

選択公理無理太郎 | 2017年5月 7日 22:24

はじめまして。唐突なコメント失礼します。

A……添え字集合
{X_a}……Aで添え字付けられた集合族(任意のa∊Aに対してX_aが定まっている)

このとき、任意のa∊Aについて、X_aが唯一つの元を持つ集合であるときでも、∏X_a≠∅を言うのに、選択公理は必要ですか?

管理人 | 2017年8月 6日 23:53

返信遅くてすみません。その場合選択公理は不要です。

匿名 | 2019年3月29日 02:10

「次の命題」が一箇所「次のの命題」になっています。

(名無し) | 2019年7月 2日 11:32

X={φ}の場合に選択関数が存在しませんね。
なぜならば、X≠φかつ∪x∈X x =φだから。

選択関数は、f:X-{φ}→∪x∈X xとするのが
普通です。

匿名 | 2019年7月 2日 11:36

誤植：記号φは∅のつもりでした。

管理人 | 2019年9月17日 18:29

修正しました。

コメント