式変形? なんか思ったことをつらつら書いただけ
例えば群論で逆元が一意であることを示すときに、xの逆元をy, zだとして
y = y1 = y(xz) = (yx)z = 1z = z
などとします。こういう、式の変形(もっときちんと言えば、文字列の形式的な変形)だけで証明が終わったりするのが「数学」って感じがしたし、こういう証明こそがよい証明だと思ってたりしたわけです。(※個人の感想です)(※なんか中1~学部くらいの頃の感想)
圏というのを触り出すと
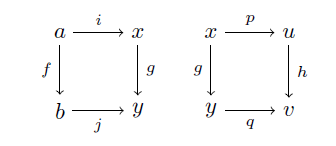
という二つの図式が可換の時に
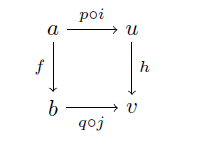
が可換であることを示せ、なんて問題が出てきて(出てきませんが)
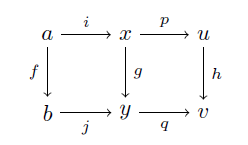
と二つの図式をくっつければそれは明らかですが,これを
h〇(p〇i) = (h〇p)〇i = (q〇g)〇i = q〇(g〇i) = q〇(j〇f) = (q〇j)〇f
と式変形でやる人はそんなにいないでしょう。(これくらいなら居るかもしれません。これくらいなら……)
図式がもっと複雑になっていくと
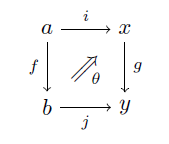
というような図式が出てきます。これは「θ」が「j〇f」から「g〇i」への「射」であることを意味しています。 意味はともかく「θ」は「射」なのです。するとこのような「射」を合成したくなることがよくあります。 そういうような「計算」を図式でやると
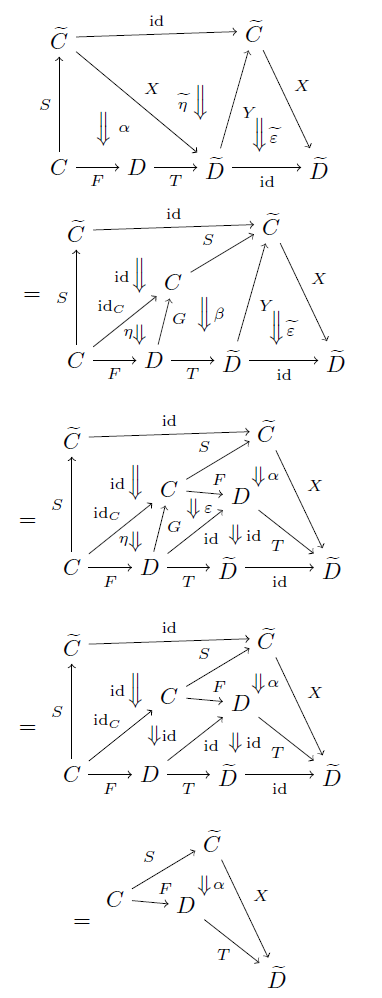
というような感じになるわけです。これをよく見ると分かるかもしれませんが(分からないかもしれませんが)、この「式変形」では文字の置き換えではなく図式の置き換えをして「式変形」をしています。そういう意味では、この計算も最初の計算も「同じ」かもしれませんが、しかし同じには全然見えません。