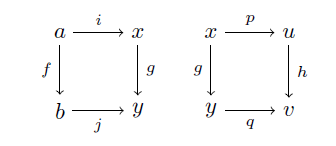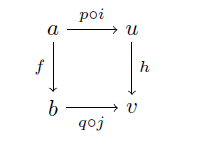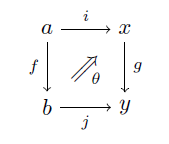algebraic dialy(数学カテゴリ)

この前2019をインストールしたばかりな気がしますが、TeX Live 2020が出たのでインストールしました。やり方はいつもと同じ感じなので省略します

さて、インストール自体はこれで良かったのですが、TeX Live 2019以前をインストール済みでtexmf-localフォルダを使用していた場合、恐らくエラーが発生するようになると思います。このフォルダの権限設定がTeX Live 2020によって変更されてしまう(?)ようです。

TeX Live2020入れてから(?) C:\texlive\texmf-local\tex\latex のファイルが一切開けなくなってる　なぜ

— alg_d (@alg_d) April 14, 2020

この表示は初めて見た　なんやねん pic.twitter.com/HTC5OuIuBI

— alg_d (@alg_d) April 14, 2020

初心者なのでこの画面も初めて見る　　所有者を自分にしてアクセス許可を自分に付けたらファイル開けるようになったけどこれはなんだ pic.twitter.com/jxwpvurfsb

— alg_d (@alg_d) April 14, 2020

C:\texlive\texmf-local\ls-R も同じく開けない状態で、このせいで自作パッケージの読み込みができない状態だった(権限設定をしたら治った) TeX Live 2020なんかおかしくない? 僕がなんか勘違いしてるのかな

— alg_d (@alg_d) April 14, 2020

権限周りの設定のことがよくわからないので、僕は必要なファイルを一個ずつ右クリックして権限を付けて回りました……

前回の通り、パソコンを新しくしたのでTeXの環境も整え直します。TeX Live 2019を入れる話は以前に書いた通りで、今回はエラーもなく1時間半程度で終わりました。

現在公開しているPDFファイルはフォントとして源ノ明朝というものを使っているので、これも入れます。これはZRさんのupLaTeX文書で源ノ明朝／Noto Serif CJKを簡単に使う方法（最新のdvipdfmxとpxchfonを使用）の通りで、要はWindows10に対して源ノ明朝というフォントをインストールすれば、あとは記事の通りTeXファイルを書くだけです。が、前のPCではこれでうまくいっていたのに今回はうまく動きませんでした。

調べた結果、Windows10 (のバージョン1809以降)ではフォントをインストールする際に「ユーザーごと」「全ユーザー」という2種類のインストール方法があり、「ユーザーごと」のインストールだとTeXではダメなようです(参考サイト: Windows 10にフォントを追加インストールする方法と注意点)。前のPCでフォントを入れたときは1809より前のバージョンで、エラーにならなかったのかもしれません。

というわけで、全ユーザーに対してフォントをインストールしなおすことで、無事に源ノ明朝が使えるようになりました。

TeX Liveインストールチャレンジ2019をしました。手順は昨年と大体同じです。

1. TeX Liveのページに行きdownloadのページから install-tl-windows.exe をDLします。
2. DLした install-tl-windows.exe を実行する(後述するように右クリックして「管理者として実行」した方が良いと思います)と次の画面が表示されるので、「Next」をクリックします。
   
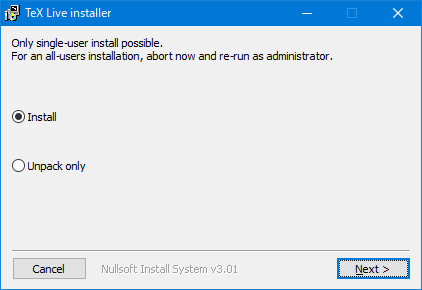
3. すると次の画面が表示されるので、「Install」をクリックすると
   
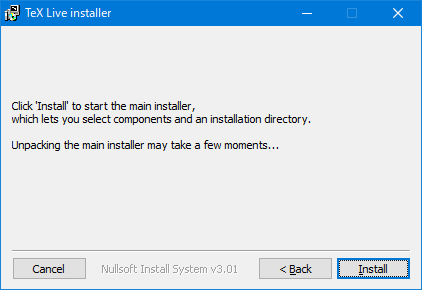
4. インストールっぽいことが始まります。
   
5. ちょっと待つとこんな画面が出てきて
   
   さらにこの画面に変わります。
   
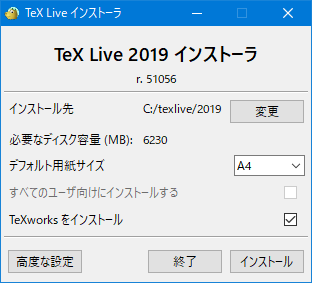
   ここで、この画像だと「すべてのユーザ向けにインストールする」がグレーアウトしていて、チェック不可になっています。これは恐らくインストーラを管理者権限で実行していないからで、install-tl-windows.exe を右クリックして「管理者として実行」すればチェックがONにできるようになります。
6. 好みの設定にしたら「インストール」をクリックすると、いつものようにインストールが始まります。
   
7. これが終わるとこの画面になるので
   
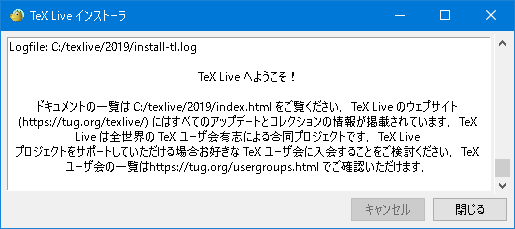
   「閉じる」をクリックすると次の画面になります。
   
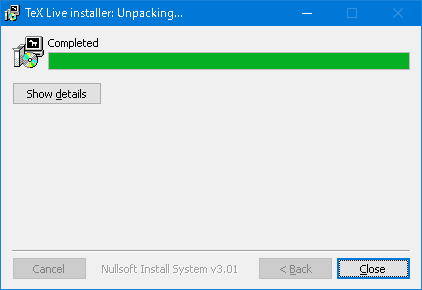
8. 「Close」をクリックしてインストール完了です。

で、うまく行くんですか? と思っている人もいるかもしれません。今年はなんと、1回目はエラーが出て失敗しましたが2回目で成功しました。成功したので昨年と同様、コマンドプロンプトを開いて「tex -version」とやってみると、確かにTeX Live 2019と出、ま、せん……。

で調べて分かったのが上記の「すべてのユーザ向けにインストールする」の話です。TeX Live 2018をインストールすると、システム環境変数のPathに必要な設定がされますが、TeX Live 2019のインストールを「すべての(ry」チェックOFFでやってしまうとユーザ環境変数の方にPathが設定されるようです(チェックONでインストールは試してないので、実際どうなのかは分かりませんが)。Windows10の仕様ではPathはシステム環境変数の方が優先される(正確な書き方ではないので、気になる人は調べてください)ようなので、これではtexを実行した時にTeX Live 2018の方が実行されてしまうわけです。

というわけで、環境変数を手で設定し直したところ、無事「tex -version」でTeX Live 2019と出るようになりました。

(2019/08/26追記: 「すべての(ry」チェックONでインストールするとシステム環境変数のPathに必要な設定がされることを確認しました。)

(2019/08/26追記その2: Windows10+upLaTeXで源ノ明朝を使う も参考にしてください。)

先日、第3回関東すうがく徒のつどいにて「全ての概念入門」というタイトルで講演をしてきました。実況のまとめもあります。実況の人たちが頑張っているので、読むとなんとなく講演内容も分かるかもしれません。

実は第2回でも講演をしているのですが、後で確認してみるとなんと同じ講演タイトルでやっていました。(これは狙っていたのではなく、講演応募後に気付きました。)

ところでこれらは同じタイトルではありますが、実は講演のテーマは違います。

第2回の「全ての概念入門」では、全ての概念=Kan拡張であり、要はKan拡張入門となっています。内容もKan拡張に絞っており、オチは「選択公理はKan拡張である」でした。(オチに選択公理を持ってくる辺りが、当時の状況を表しているなという感じがします。)

一方で第3回の「全ての概念入門」は、まさに「全ての概念」がテーマになっています。どういうことかというと、圏論には様々な概念があるわけですが(そして、それらが全てKan拡張で「書ける」というのがすべKanです)、それらは互いに関係があります。

• 普遍射が存在すれば随伴が得られる
• 逆に随伴が存在すれば普遍射が得られる
• 特に余極限が存在すれば対角関手の左随伴が得られる
• 逆に対角関手の左随伴があればそれは余極限を与える
• 普遍射は表現可能関手を使って定義できる
• 特に余極限は表現可能関手を使って定義できる
• Kan拡張は随伴である
• 逆に随伴はKan拡張で書ける
• Kan拡張は余極限で計算できる
• 逆に余極限はKan拡張である
• ……

というわけで圏論はまさに「全ての概念は全ての概念である」とでも言うべき状態になっており、これを説明するというのが今回のテーマでした。

これは勿論当サイトのPDFを読めば分かることですから、詳しく知りたい人は是非PDFを読んで勉強してみてください。

いつの間にかTeX Live 2018がリリースされていたようなので、Windows10にインストールしてみました。

1. TeX Liveのページに行きdownloadのページから install-tl-windows.exe をDLします。
2. DLした install-tl-windows.exe を実行すると次の画面が表示されるので、「Next」をクリックします。
   
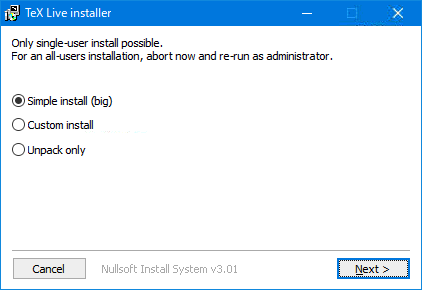
3. すると次の画面が表示されるので、「Install」をクリックすると
   
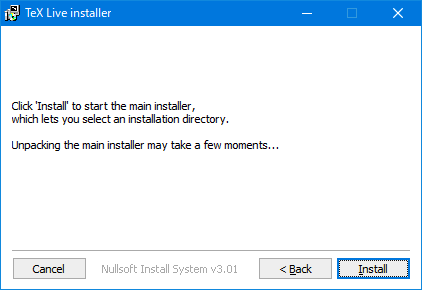
4. インストールっぽいことが始まります。
   
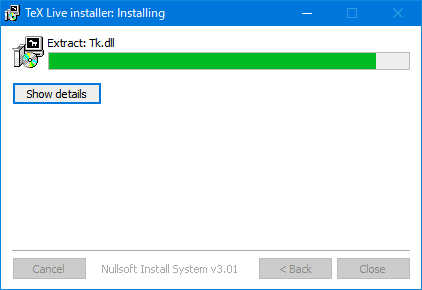
5. ちょっと待つとこの画面が出てくるので「次へ」をクリックします。
   
6. この画面になりますが、「少し時間がかかります!」とのことなので待っていると
   
7. こうなるので「次へ」をクリックします。
   
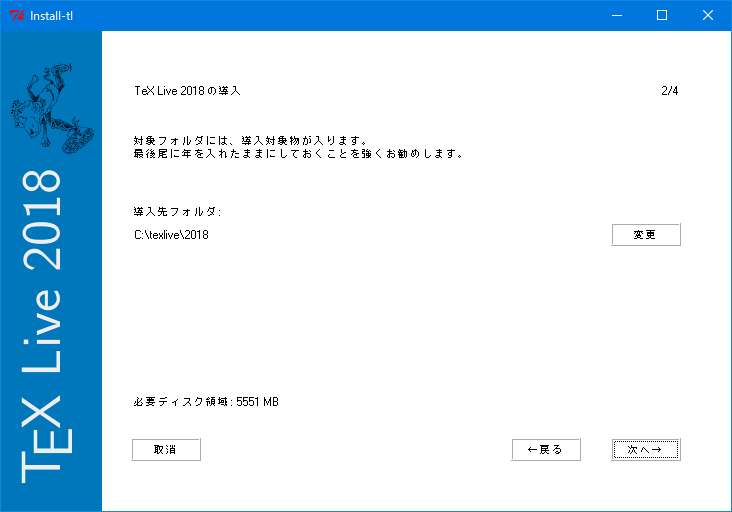
8. この画面になるので、好みの設定にします。
   
   メニューショートカットっていうのは、スタートメニューに出来るこれですかね?
   
   TeXworksフロントエンドというのはよく分かりませんが、私はTeXworksは使わないのでチェックをOFFにしました。
9. 次に進むとこうなるので「導入」をクリックすると
   
10. 長いインストールが始まります。これが終わると
    
11. この画面になるので、「終了」をクリックしてインストール終わりです。
    
12. コマンドプロンプトを開いて「tex -version」とやってみると、確かにTeX Live 2018と出て、インストールができてるっぽいことが分かります。
    

と、うまく行けばいいんですけどね～。実際の所、私の環境では、5回くらいやっても

というエラーが途中で出てしまい、インストールできませんでした。 3GBくらいある texlive2018-20180414.iso をDLして、その中にある install-tl-windows.bat を実行したらうまくインストールできました(手順は上に書いたのと大体おなじ)。

Category Theory Advent Calendar 2017の3日目です。

Category Theory Advent Calendar 2017 3日目 PDF

「選択公理⇒排中律」です。参考文献で上げているJohnstoneを読んで昔証明を書いたのですが、まだトポスのページが無くて出せていなかったものを引っ張り出してきたものになります。多少ギャップがありますが仕方ない。

Category Theory Advent Calendar 2017の2日目「明日使える? Kanリフトの話」です。

Category Theory Advent Calendar 2017 2日目 PDF

Category Theory Advent Calendar 2017の1日目ということで、Math Advent Calendar 2017 1日目に対抗してp進整数環の話を書きました。

Category Theory Advent Calendar 2017 1日目 PDF

ちなみに、代トポのサイトを眺める日課でFractalのページを発見して、こういうのもあるのかと思って書きました。

例えば群論で逆元が一意であることを示すときに、xの逆元をy, zだとして

y = y1 = y(xz) = (yx)z = 1z = z

などとします。こういう、式の変形(もっときちんと言えば、文字列の形式的な変形)だけで証明が終わったりするのが「数学」って感じがしたし、こういう証明こそがよい証明だと思ってたりしたわけです。(※個人の感想です)(※なんか中1～学部くらいの頃の感想)

圏というのを触り出すと

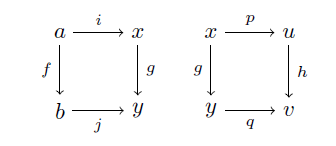
という二つの図式が可換の時に

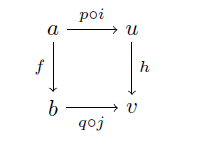
が可換であることを示せ、なんて問題が出てきて(出てきませんが)

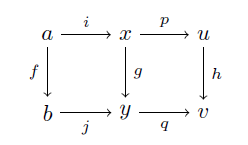
と二つの図式をくっつければそれは明らかですが，これを

h〇(p〇i) = (h〇p)〇i = (q〇g)〇i = q〇(g〇i) = q〇(j〇f) = (q〇j)〇f

と式変形でやる人はそんなにいないでしょう。(これくらいなら居るかもしれません。これくらいなら……)

図式がもっと複雑になっていくと

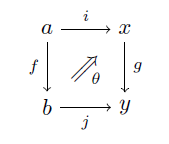
というような図式が出てきます。これは「θ」が「j〇f」から「g〇i」への「射」であることを意味しています。 意味はともかく「θ」は「射」なのです。するとこのような「射」を合成したくなることがよくあります。 そういうような「計算」を図式でやると

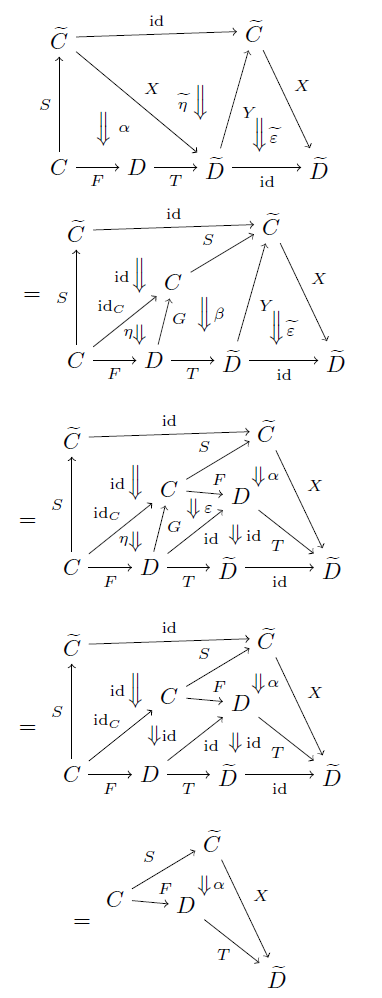
というような感じになるわけです。これをよく見ると分かるかもしれませんが(分からないかもしれませんが)、この「式変形」では文字の置き換えではなく図式の置き換えをして「式変形」をしています。そういう意味では、この計算も最初の計算も「同じ」かもしれませんが、しかし同じには全然見えません。

この記事はTeX & LaTeX Advent Calendar 2015 4日目です。 3日目は@p_typoさんの今さら人に聞けないローマ数字とその組み方でした。 5日目は@neruko3114さんのLaTeXで得られる出力をMSWordのそれに近付けようとするためにです。

皆さんも普段からTeX/LaTeXで色々命令を定義して使っていると思います。私も色々定義していますが、今回は初心者大歓迎(重要)の「今さら人に聞けない、TeXのキホン」がテーマとのことですので、私が普段使っている命令を紹介することで、「TeXのキホン」が理解できたらいいなぁと思います。

私がLaTeXを使うのは数学に関する文書を作るためですが、最近は特に圏論について色々書いているので、射(写像)の合成を頻繁にします。2つの射(写像) f: x→y と g: y→z の合成は g\circ f と書くと思いますが、「fを適用して、gを適用する」のに g ⇒ f の順でタイピングするのは非常に難しいです(まあ手書きするときも同じ問題があるのですが)。

そこで、引数を f ⇒ g の順で与えたら g\circ f を出力するような命令(ここでは \compo とすることにする)を作ってみたいと思いました。

簡単にやるには \newcommand{\compo}[2]{#2\circ #1} とでも書けば、 \compo{f}{g} で g\circ f が出ます。が、これだと3つ合成する場合 \compo{\compo{f}{g}}{h} となり、書きやすいとは言えません。 ここは \compo{f}{g}{h} で h\circ g\circ f と出て欲しいです。

このように引数の数を可変にしたい場合どうすればいいかというと、次のような方法で実現できることが分かります。 まず \compo を \newcommand{\compo}[2]{\compo{#2\circ #1}} のような定義にします。すると、\compo{f}{g} と書いた場合 \compo{g\circ f} と展開されるわけです。つまり \compo{f}{g}{h} と書いた場合は \compo{g\circ f}{h} 即ち \compo{h\circ g\circ f} と展開されます。ただ、これでは処理がいつまで経っても終わらない、というか命令 \compo から見るとどこまでが引数なのか分からないので、終わりを明示してやる必要があります。

そこで、とりあえず「第二引数に \relax が指定された場合はそこで処理を終了する」ということにします(\relax が大変便利な命令であることは2日目の\relax の使い方 12連発で見ましたね!!)。つまり、\compo を

• \compo{f}{\relax} の場合: f
• \compo{f}{g} の場合: \compo{g\circ f}

と出力するように変えてやるわけです。こうすれば \compo{f}{g}{\relax} は g\circ f となるし、\compo{f}{g}{h}{\relax} は h\circ g\circ f となります。TeXにはいわゆるif文的な命令があるので、それを使えばこれはできそうです。なのでそれをやってみると、以下のようにすれば良さそうです……

\newcommand{\compo}[2]{
    \ifx#2\relax
        #1
    \else
        \compo{#2\circ #1}
    \fi
}

(※ \ifx#2\relax の部分が「#2 が \relax に等しいならば」を表します。)

が、これはやってみると上手くいきません。展開順がどうとか色々あってそんなに簡単ではないようです。で、色々調べて試行錯誤してみたところ、次のように書くと上記が実現できることが分かります。

\newcommand{\compo}[2]{
    \def\compox{\compo{#2\circ #1}}
    \ifx#2\relax 
        #1 
    \else 
        \expandafter\compox
    \fi 
}

みんなの大好きな \expandafter ですね!!!! (\expandafter についてはここでは触れませんが、「TeXのキホン」なので \expandafter のプロが何日目かに解説してくれるでしょう)

これでもいいですが(いや、よくないところはあるんですが)、これだと一々 \relax を後ろに付ける必要があり、面倒だし忘れそうです。そこで一番後ろに \relax を付加する命令も用意しましょう。どういうことかというと、新しい命令 \componew を \newcommand{\componew}[1]{\compo#1{\relax}} と定義します。こうすると例えば \componew{{f}{g}} とすれば \compo{f}{g}{\relax} となるので g\circ f が出力されるし、 \componew{{f}{g}{h}} とすれば h\circ g\circ f が出力されます。(ただ、中括弧が二重になってしまうので、どっちもどっちとも言えますが…。) ただ、1日目の完全攻略! LaTeX 命令の"引数の規則"の通り、 \componew{{f}{g}{h}} は実は \componew{fgh} と書けるので、\componew の方が便利だと思っています。

と、こんな感じで随分前に命令を作ってずっと使っています(特に圏論のPDFでは使いまくっています)が、便利だし特に問題も起きてないので、折角のこのタイミングで書いてみました(あと、公開すればTeXのプロがまずい点を指摘してくれると思って…)。上で作った命令は説明用のものなので、実際使っているのは以下の通りです。(下記はスタイルファイル用になっているのでスタイルファイルに書いてください)

\def\compo#1{
    \algd@compo#1\algd@end
}

\def\algd@compo#1#2{
    \def\algd@temp{\algd@compo{#2 \circ #1}}
    \ifx#2\algd@end
        #1
    \else
        \expandafter\algd@temp
    \fi
}

\def\algd@end{\algd@end@}

「全ての概念はKan拡張である」この言葉はそれなりに有名になったと思いますが、これがどういう意味なのか、私なりの見解をここに書いておきたいと思います。

まず「すべての概念はカン拡張である(all concepts are Kan extensions)」というのは圏論の教科書『圏論の基礎(Categories for the Working Mathematician)』(以下、この本をCWMと呼ぶ)に書いてある言葉です。CWMの前書き(初版への序)には以下のように書いてあります。

圏論の基本概念が終わりの二章にまとめられている．たとえば極限の，より差し迫って必要となる性質，特にフィルター極限の性質，「エンド」の計算，そしてカン拡張の概念，といったものである．カン拡張は随伴の基本的構成の，より深い形式である．圏論のすべての概念はカン拡張である，ということを見て本書は終わる(第X章第7節)．

この第X章第7節のタイトルは「すべての概念はカン拡張である」であり，簡単にいうと次のようなことが書いてあります。

1. 余極限は左Kan拡張である(双対的に極限は右Kan拡張である)
2. 随伴はKan拡張である
3. 米田の補題はKan拡張である

確かに、圏論では大抵の概念が普遍性(極限や余極限)や随伴で定義されるので、そういう意味で全ての概念はKan拡張であると言えそうです。ですが、そう言われても「それで?」としか思えないのではないでしょうか。

実際の所、Kan拡張というのは圏論をやっていると至る所で現れるものであって、そういう意味で「全ての概念はKan拡張」なのです。ところが、そういう風に書いてある本があまり無いので、言われないと気付かなかったりします。そこで「全ての概念はKan拡張である」ことを示そうというのが圏論のページの目的でもあります。なのでこのページを読んでもらえればいいのですが、折角なのでその中からいくつか簡単に紹介しましょう。

まず、定理「任意の前層は表現可能関手の余極限で書ける」。CWMでは第III章第7節に同様の定理の証明があります。この証明は、なんか余極限が突然与えられてそうなる、というような証明です。この証明を読んだだけだと何故こういう余極限を考えればよいのか分かりませんが、それはKan拡張を考えれば直ちに分かることなのです。

次に、単体的集合から位相空間を作る「幾何学的実現」と呼ばれる操作があります。これは大抵余極限で定義され、色々な性質を持つ事が分かりますが、何故このような余極限を考えればいいのか分かりません。実はこれもKan拡張を知っていれば、ただの各点Kan拡張をしただけだということが分かるのです。(なおCWMでは第IX章第6節にコエンドを使った定義が載っていますが、これはコエンドを使った各点Kan拡張です。)

最後に「随伴関手定理」。CWMだと第V章第6節です。この定理では解集合条件(Solution Set Condition)という条件が出てきて、この条件がなんなのか良くわかりませんが、これも随伴がKan拡張であることを知っていれば、この条件があれば各点Kan拡張ができるという定理だということが分かります。

関西すうがく徒のつどいで発表してきた。

今回は二日とも何故かのあん氏というフォローすらしてなかった人とずっと遊んでいた感がある。うける

懇親会では、持参したNEW GAME!を持って皆にひたすら買えと言っておいた(売っているとは言っていない)。

なお、つどい一日目にalg_dを名乗っていたのはワヘイヘイですので。

最近2-categoryというのを調べていたのですが、パッと見面白そうなので勉強していた所どんどんつらみが出てきました。

圏であって、各Hom(X, Y)がまた圏になっているようなものを2-category(もしくはstrict 2-category)といいます。(例は圏の圏Cat。)ただし、射の合成から得られるHom(Y, Z)×Hom(X, Y)→Hom(X, Z)は関手になる、という条件もつけます。

これはこれでいいのですが、2-categoryは圏ですから、当然、射の合成は結合律を満たします。この結合律というのは言い換えれば，2通りの合成から得られる2つの関手Hom(Z, W)×Hom(Y, Z)×Hom(X, Y)→Hom(X, W) が一致するということです。しかし、関手が一致するという条件はかなり強いです。そこで、これを「関手が自然同型である」という条件に弱めることを考えることができます。そういうのをbicategory(もしくはweak 2-category)といいます。

ここで面白いのは、任意のbicategoryは2-categoryと「bicategoryの意味で同型」となるという定理があることです。

この証明は米田から得られます。つまり、まずbicategory Bに対してCat^Bopというのを考えます。実は、これは2-categoryとなります。そして米田埋込y: B→Cat^Bopを考えることができます。(ちなみに米田の補題のbicategoryバージョンが成り立ちます。)このときyの像(?)をC⊂Cat^Bopとすればこれも2-categoryでyが同型B→Cを与えるわけです。

この証明を追い始めてみたらつらすぎてつらいという近況報告

Mathematics Advent Calendar 2013

数学徒アドベントカレンダー26日目の記事です ! ! 　いや、本当は25日目が空いてたのでそこにしようかと思ってたら双対性に詳しいまれいんさんが25日目もやるという素晴らしい行動に出たので、じゃあ26日目でいいやということになりました。ちなみに、形式上は6日目の記事になります。

内容は、モチのロンで選択公理で、タイトルは「選択公理が証明できないこと」です。PDFファイル

元々は「選択公理の独立性」とするつもりでしたが、これをやろうとすると開始数ページでGödelのLを構成し終えるという誰も分からない記事になりそうだったので、半分諦めることにしました。最初に書いてあることを認めてもらえれば特に数学基礎論を知らなくても雰囲気は伝わるのではと思います。ZFCの定義くらいは知ってたほうが読みやすいとは思いますが。本当は強制法も入れようかと思ってたんですがわけが分からなくなりそうだったのでやめました。

ちなみに全部ちゃんと証明をつけたバージョンのPDFを書くプロジェクトも進行しています。そっちはトポスまで書くつもりですが…あれよくわかんないので #つらい

選択公理についてググると以下のようなページがヒットするわけですが、この説明は良くないと思うのでここで少し説明を書いておこうと思います。

選択公理 - Wikipediaより

この公理を認めると、一つの球を有限個に分割してそれぞれを集めて元の球と同じ体積の球を二つ作ることができるという、常識では考えられないことが起こる（バナッハ＝タルスキーのパラドックス）。従って、この公理の妥当性に疑問を持つ数学者もいる。しかし、この公理を用いないと、証明できない事柄が多くでてきてしまう。

選択公理: 役に立たない数学用語事典より

これに関してはさまざまな解釈、打開策が考えられたが、実は現在も誰もが納得するすっきりとした結論が出ているわけではない。選択公理はいまなお現代数学ののどの奥に小骨のように突き刺さっている。

選択公理でググってこういう説明がすぐ見つかるの、ヤバイと思うんですよね。選択公理の妥当性に疑問を持っているような数学者はいないと思うし(居たらごめんなさい)、選択公理は認めるべきというのが誰もが納得するすっきりとした結論だと思います。Banach-Tarskiについては後述。

まず、選択公理とは「 { X_λ }_λ∈Λを空でない集合からなる族とすれば、直積 Π_λ∈ΛX_λも空でない」という主張でした。これが成り立つのは直感的には明らかだし、逆に言えばこれが成り立たないなんてのは(Banach-Tarskiなんかよりもよっぽど)直感に反していると思います。

選択公理を認めなければならないのは、普通に数学をやっている中で普通に現れるからです。一番有名と思われるのは「無限集合 X は可算無限部分集合を含む」の証明でしょう。この証明は以下の通りです。

まず a₀∈X を取ります。X は無限だから X＼{ a₀ } は空ではありません。よって a₁∈X＼{ a₀ } が取れます。 X＼{ a₀, a₁ } も空でないから a₂∈X＼{ a₀, a₁ } が取れます。これを繰り返していけば可算無限集合 { a₀, a₁, a₂, a₃, … }⊂X が得られます。

この証明は実は選択公理を使っています。それは元 a_n∈X＼{ a₀, …, a_n-1 } を取るという操作を無限回行わなければならないからです。そして、「この命題は選択公理なしでは証明できないこと」が証明されています。こういうような操作は数学の様々なところで行われています。例えば関数解析なんかだと「各n∈Nについて～～～を満たす x_n∈X を取れば、これはCauchy列をなすから極限 x が存在し、……」なんてことを何度もやりますが、この x_n∈X を取るというのは選択公理を使っています。(選択公理を使わずに取れる場合もあります。)

これ以外にも、証明に選択公理が要る命題はたくさん知られていて、それはこのサイトの選択公理のページにも書いてあるとおりです。例えば線型空間の基底の存在、体の代数閉包の存在、コホモロジーの性質、Hahn-Banachの定理、等々…。

さて、選択公理が直感に反すると言われるのは何故かといえば、既に引用したようにBanach-Tarskiが原因でしょう。これは、そもそも定理を「一つの球を有限個に分割してそれぞれを集めて元の球と同じ体積の球を二つ作ることができる」という風に「日本語で」そのまま解釈するのが間違いでしょう。

例えば、|N| = |Q| であることを「自然数の個数と有理数の個数は同じ」と表現することがありますが、これを見て「自然数は有理数で、自然数でない有理数があるんだからこれはおかしい! 直感に反する!」と言う人は居ないでしょう。それは「個数が同じ」というのは「全単射が存在する」という意味だと分かっているからです。Banach-Tarskiの場合も同じです。

「一つの球を有限個に分割して」とありますが、これは正確に述べると、B = { (x, y, z)∈R³ | x^2+y^2+z^2≦1 } を球体としたときに B = X₀∪X₁∪…∪X_n (i≠jならば X_i∩X_j= ∅) と書けるということです。これは集合として「有限個に分割できる」ということです。例えば X₀ を有理数全体、 X₁ を無理数全体とすれば R = X₀∪X₁、X₀∩X₁= ∅ です。つまり、この分割はBanach-Tarskiが言っている「有限個に分割」の条件を満たしているのです。しかし、物理的にこれを「有限個の分割」というでしょうか? Banach-Tarskiでは球体をこれよりももっとヤバイ方法で分割しているので、そりゃ球体が増えるくらい起こりえるわけです。

ところで、Banach-Tarskiの証明はそれなりの長さがありますが、その内容は殆ど「群」や「群が作用している集合」についての議論であって、選択公理は関係ありません。そして選択公理を使うのは「商集合の代表系」を一回とるだけです。つまり、実はBanach-Tarskiは選択公理とはあまり関係がないのです。証明を見ると分かりますが、Banach-Tarskiはどちらかというと自由群 F₂ の性質から来ているような感じがします。

所で

選択公理よりも弱い公理として、可算選択公理というものも考えられている。これは選択公理の成立する範囲を可算濃度以下に限定したものだ。この公理を採用すると非常に都合がよい。「選択公理がないと証明ができない」とされる正当な定理のほとんどは、可算選択公理で証明される。「選択公理を用いると証明できるが、感覚的に奇妙である」とされる変な定理の多数（全てではない）は、可算選択公理では証明されない。結局、選択公理のかわりに可算選択公理を採用すると、非常に自然な（納得の行く）数学体系ができる。

というようなことが書かれていますが、「選択公理がないと証明ができない」とされる正当な定理のほとんどは、可算選択公理では証明できないが正しいと思われます。実際、このサイトに載っている「選択公理と同値な命題」は勿論可算選択公理では証明できないからです。また、「可算無限まで認めるなら任意の無限でも認めていいでしょ」という感じがします。

ちなみに、Hahn-Banachを認めるとBanach-Tarskiが証明できますので、どっちにしろBanach-Tarskiについては諦めてください。