定義Cを圏とする．

1. 対象 I∈C が入射的(injective)
   ⇔関手 Hom_C(-, I) がモノ射をエピ射に送る
2. 対象 P∈C が射影的(projective)
   ⇔関手 Hom_C(P, -) がエピ射をエピ射に送る(エピ射を保つ)
3. C が十分豊富に入射的対象を持つ(enough injective)
   ⇔任意の対象 X∈C に対し，ある入射的対象 I∈C とモノ射 f: X→I が存在する． これを EI(C)で表す．
4. C が十分豊富に射影的対象を持つ(enough projective)
   ⇔任意の対象 X∈C に対し，ある射影的対象 P∈C とエピ射 f: P→X が存在する． これを EP(C)で表す．

例 集合と写像のなす圏 Set の場合．

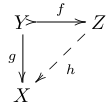集合Xが入射的
⇔任意の単射 f: Y→Z と任意の写像 g: Y→X に対しある写像 h: Z→X が存在して g=hf となる．

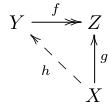集合Xが射影的
⇔任意の全射 f: Y→Z と任意の写像 g: X→Z に対しある写像 h: X→Y が存在して g=fh となる．

命題1 EI(Set)である．

証明任意の空でない集合が入射的だからである．

定理2 次の命題は(ZF上)同値

1. 選択公理
2. 任意の集合が射影的．
3. 任意の集合 X に対して，射影的な集合 Y が存在して X⊂Y．

証明 (1 ⇒ 2) Xを任意の集合とする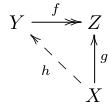． 任意の全射 f: Y→Z と任意の写像 g: X→Z を取る． f が全射だから各 x∈X に対し f^-1(g(x)) は空でない． そこで { f^-1(g(x)) }_x∈Xに選択公理を適用して 選択関数 h: X→∪_x∈X f^-1(g(x))⊂Y を得る． すると，h(x)∈f^-1(g(x)) だから fh=g である．

(2 ⇒ 3) Y=Xとすればよいから明らか．

(3 ⇒ 1) 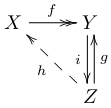全射の右逆写像の存在を示す．f: X→Y を全射とする．仮定3により，射影的な集合 Z で Y⊂Z となるものが存在する． a∈Y を一つ取る．写像 g: Z→Y を

z∈Y のとき　g(z) := z
そうでないとき　g(z) := a

で定める．i: Y→Z を包含写像とすれば明らかに gi = id_Y である．Z が射影的だから，ある写像 h: Z→X が存在して fh=g を満たす．このとき k := hi: Y→X と置けば fk = fhi = gi = id_Y である．

例 R を単位的可換環とし，R-加群とR-準同型のなす圏 R-Mod を考える．

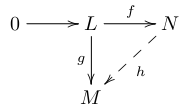R-加群 M が入射的
⇔任意の単射準同型 f: L→N と任意の準同型 g: L→M に対し， ある準同型 h: N→M が存在して g=hf となる．

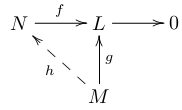R-加群 M が射影的
⇔任意の全射準同型 f: N→L と任意の準同型 g: M→L に対し， ある準同型 h: M→N が存在して g=fh となる．

アーベル群と群準同型のなす圏 Ab を考える．(Ab = Z-Modである．)よく知られているように，EI(Ab)とEP(Ab)が成立している． EP(Ab)のよく知られた証明は

1. 任意のアーベル群Aに対し，自由アーベル群Bと全射準同型 f: B→A が存在する．
2. 自由アーベル群は射影的

という手順で与えられる． EI(Ab)の証明も同じように

1. 任意のアーベル群Aに対し，可除アーベル群Bと単射準同型 f: A→B が存在する．
2. 可除アーベル群は入射的

という手順で与えられる．

どちらの証明も1は選択公理を使わずに(ZFで)できる．問題は2である．

定理3 次の命題は(ZF上)同値

1. 選択公理
2. 任意の単位的可換環 R とR-加群 M に対して次が成り立つ．

   任意のイデアル I⊂R と任意の準同型 φ: I→ M に対して
   ある準同型 ψ: R→M が存在して ψ|_I=φ となる．
   ⇒ Mが入射的

3. 任意の単項イデアル整域 R に対して，可除R-加群は入射的
4. 可除アーベル群は入射的

証明(1 ⇒ 2) 単射準同型 f: L→N と準同型 g: L→M を取る．f により L⊂N とみなす．集合

X := { (A, h) | L⊂A⊂N は部分加群，h: A→M, h|_L=g }

を考える．(L, g)∈X だから X≠ ∅ である．X に順序≦を

(A, h)≦(B, k) ⇔ A⊂B, k|_A=h

で定めると(X, ≦)は帰納的順序集合となり，Zornの補題より極大元(A, h)∈Xが存在する．

A ⊊ Nと仮定する．元 x∈N＼A が取れる．B := A+Rx と置く．I := { r∈R | rx∈A }⊂R はイデアルである． 準同型φ: I→M をφ(r) := h(rx) で定める．仮定からψ: R→M が存在してψ|_I=φである．さて，準同型 k: B→M を任意の a∈A と r∈R に対して k(a+rx) := h(a)+rψ(1) と定める．これはwell-definedである．

このとき k|_A=h だから (A, h)≦(B, k) である． 明らかに A ⊊ B だから (A, h) の極大性に矛盾する． 故に A=N が分かり，g=hf である．

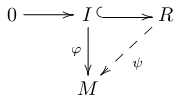
(2 ⇒ 3) R を単項イデアル整域，M を可除R-加群とする．任意のイデアル I⊂R と任意のφ: I→M を取る．仮定2によりψ|_I=φとなる準同型ψ: R→M を見つければよい．I=0 のときは自明だから I≠0 とする．R が単項イデアル整域だから，ある α(≠0)∈R を使って I=(α) と書ける．φ(α)∈M なので M の可除性により，ある m∈M が存在して φ(α)=αm となる．そこでψ: R→M をψ(r) := rm で定めれば ψ(α) = αm = φ(α) だからψ|_I=φである．

(3 ⇒ 4) Zは単項イデアル整域である．

(4 ⇒ 1) 選択公理と同値な次の命題を示す．

集合族が「任意のλ∈Λに対し |X_λ|≧2 」を満たすとき， Λ上の関数 f が存在して任意のλ∈Λに対して ∅ ≠f(λ) ⊊ X_λかつ|f(λ)|<∞ となる．

同値性の証明はthe Axiom of Multiple Choiceの定理2を参照．

集合族が「任意のλ∈Λに対し |X_λ|≧2 」を満たすとする．これらは互いに素としてよい．X := と置く． X を基底とする Q 上の線形空間を V とする．以下これを可除アーベル群として考える H := < x-y | あるλ∈Λが存在して x, y∈ X_λ >⊂V は部分群で，D := V/H も可除アーベル群になる．v∈V の属する同値類を [v]∈D で表す．任意の x, y∈X_λ に対し [x]=[y] である．よって [x]∈D は x∈X_λ の取り方によらず，λのみから定まる．そこで [λ] := [x] と定める． Λで生成される自由アーベル群を F とする．

|X_λ|<∞ のとき m_λ := |X_λ|
|X_λ|=∞ のとき m_λ := 2

として，f(λ) := m_λλと g(λ) :=[λ] により，単射準同型 f: F→F と準同型 g: F→D が得られる．仮定4より可除アーベル群 D は入射的，よって準同型 h: F→D でhf=g を満たすものが存在する．λ∈Λに対して

[λ] = g(λ) = h(f(λ)) = h(m_λλ) = m_λh(λ).

h(λ)∈D = V/H だから，あるv_λ∈Vを使って h(λ)=[v_λ] と書ける．v_λ = Σ_x∈Xα^(v_λ)_xx (α^(v_λ)_x∈Qは有限個を除いて0) と一意的に書けて，このとき

[λ] = m_λh(λ) = m_λv_λ] =[m_λv_λ] =[Σ_x∈Xm_λα^(v_λ)_xx].

任意の y∈X_λ を一つ取れば取れば [λ] = [y] だったから [y] = [Σ_x∈Xm_λα^(v_λ)_xx] である． 故に(m_λα^(v_λ)_y-1)y+Σ_x≠ym_λα^(v_λ)_xx∈H だから， 任意の x∈X_λ に対して m_λα^(v_λ)_x∈Z となる． よってある n_x∈Z が存在して α^(v_λ)_x = n_x/m_λ と書ける．このとき

[Σ_x∈Xλm_λα^(v_λ)_xx] = [Σ_x∈Xλn_xx] = Σ_x∈Xλn_x[x] = Σ_x∈Xλn_x[λ]

だから Σ_x∈Xλn_x = 1 である． 従って α^(v_λ)_x∈(1/m_λ)Z かつ Σ_x∈Xλα^(v_λ)_x = 1/m_λ が分かった．そこで

n_λ := min{ n>0 | あるx∈X_λに対して α^(v_λ)_x≡n/m_λ (mod 1) }
F_λ := { x∈X_λ | α^(v_λ)_x≡n_λ/m_λ (mod 1) }

とすれば(これらは v_λ の取り方によらない)，F_λ⊂X_λ, 0<|F_λ|<∞である．

あとは F_λ ⊊ X_λ を示せばよい．これは |X_λ|=∞ のときは明らかだから |X_λ|<∞ としてよい．F_λ=X_λ と仮定する．即ち任意の x∈X_λ に対し α^(v_λ)_x≡n_λ/m_λ (mod 1)である．このとき1/m_λ = Σ_x∈Xλα^(v_λ)_x≡(n_λ/m_λ)m_λ≡0 (mod 1) となりm_λ>1に矛盾する．

定理4 次の命題は(ZF上)同値

1. 選択公理
2. 任意の環 R とR-加群の族 { M_λ }_λ∈Λ に対して

   全てのλ∈Λについて M_λ が射影的 ⇒ M :=⊕_λ∈Λ M_λ が射影的

3. 任意の環 R に対して，任意の自由R-加群は射影的
4. 任意の自由アーベル群は射影的
5. ある環 R が存在して，任意の自由R-加群は射影的

証明(1 ⇒ 2) 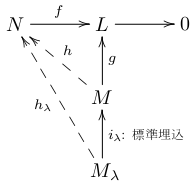任意の全射準同型 f: N→L と準同型 g: M→L を取る． λ∈Λに対し i_λ: M_λ→M を標準的な埋め込みとして， A_λ := { h_λ: M_λ→N | fh_λ = gi_λ } と置く．M_λは射影的だから A_λ≠ ∅ である．よって選択公理により (h_λ)∈Π_λ∈Λ A_λ が取れる．すると直和の普遍性から h: M→N でhi_λ=h_λ となるようなものが存在する．このとき fhi_λ = fh_λ = gi_λ だから f=g である．

逆「 M が射影的 ⇒ 各 M_λ が射影的」は選択公理によらず成り立つ．

(2 ⇒ 3) R 自身をR-加群とみるとき，R は射影的．よって自由R-加群 ⊕R は射影的である．

3⇒4 と 4⇒5 は明らか．

(5 ⇒ 1) 選択公理と同値なAMCを示す．

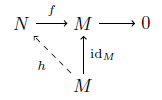
を互いに素な非空集合の族とする．と置く．Λで生成される自由R-加群を M とし，X で生成される自由R-加群を N とする．X_λの元をλに写す全射 X→Λ から自然に 全射準同型 f: N→M が得られる．仮定より自由R-加群 M は射影的，よってある h: M→G が存在して fh=id_M となる．λ∈Λ⊂M に対し h(λ) = Σ_x∈Xα_{λ, x}x (α_{λ, x}∈Rは有限個を除いて0) と書く．λ = fh(λ) = Σ_μ∈Λ (Σ_x∈Xμα_{λ, x})μ であり， 表現の一意性から Σ_x∈Xλα_{λ, x}=1 となる．故に F_λ := { x∈X_λ | α_{λ, x}≠0 }⊂X_λは空でない有限集合である．

定理5 k を体とするとき，次の命題は同値

1. 選択公理
2. k-線型空間は入射的．
3. k-線型空間は射影的．
4. 基底を持つk-線型空間は射影的．

証明 (1 ⇒ 2)体は単項イデアル整域で，線型空間は可除だから定理3の条件3より明らか．

(2 ⇒ 1)選択公理と同値な「任意の k-線型空間 V とその部分空間 A に対し， A の補空間 B が存在する」を示す．

V を k-線型空間とし A⊂V を部分空間とする．仮定(2)より A は入射的である．故に，次の図式を可換にする線型写像 f: V→A を得る．

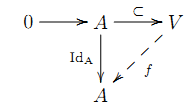
B := ker f とすれば A⊕B = V である．

(1 ⇒ 3) V を k-線型空間 V とする．選択公理により V の基底が存在し， V は自由 k -加群である．故に定理4の条件3により V は射影的である．

(3 ⇒ 4)明らか．

(4 ⇒ 1)AMCを示す． { X_λ } _λ∈Λ を互いに素な非空集合の族とする． X := ∪_λ∈ΛX_λ と置く． f: X→Λ を f(x) := (x∈X_λ となる λ ) で定める．集合 B に対して k^(B) で B を基底とする k-線型空間を表すと， f から線型写像 f^-: k^(X)→k^(Λ) が自然に得られる． f が全射だから， f^- も全射である．仮定(4)より， k^(Λ) は射影的，よって次の図式を可換にする線型写像 g: k^(Λ)→k^(X) が存在する．

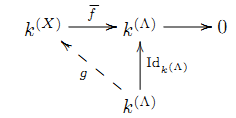
λ∈Λ に対し g(λ)=Σ_x∈Xa(x, λ)x と一意に表す．この表示を使って

F_λ:= { x∈X_λ | a(x, λ)≠0 }

と置く． Σ_x∈Xa(x, λ)x は有限和だから F_λ も有限集合である．また

λ
= id_k^(Λ)(λ)
= f^-(g(λ))
= f^-(Σ_x∈Xa(x, λ)x)
= Σ_x∈Xa(x, λ)f^-(x)
= Σ_λ∈Λb_λλ　(b_λ := Σ_x∈Xλa(x, λ))

となるから，表現の一意性より a(x, λ)≠0 となる x∈X_λ は存在する．即ち F_λ≠ ∅ ．故にAMCが成り立つ．

では EI(Ab) や EP(Ab) そのものは ZF で証明できるのであろうか，というと以下のことが知られている．

定理 非自明な入射的アーベル群の存在は ZF で証明できない．よって EI(Ab) は ZF で証明できない．

また， EP(Ab) からDMC(従属選択公理についてを参照)が従うことが知られている．ここから EP(Ab) が ZF で証明できないことが分かる．

定理 EP(Ab) ⇒ DMC

証明 DMCと同値な次の命題を示す．

{ X_n }_n=0^∞ を互いに素な非空集合の族で， |X₀|=1 とする． X := ∪_n=0^∞X_n として，全射 f: X→X は「x∈X_n+1 に対して f(x)∈X_n」を満たすとする．このときある { F_n }_n=0^∞ が存在して F_n⊂X_n, 0 < |F_n| < ∞, f(F_n+1)=F_n となる．

これを示すため， G を X で生成される自由アーベル群とする． X₀={ x₀ } と書く． EP(Ab) により射影的アーベル群 P と全射準同型 f: P→G が存在する． g: G→G を

g(x) := 0　(x∈X₀)
g(x) := f(x)　(x∈X＼X₀)

により定まる準同型とする．g は全射である．よって gf も全射である．

P が射影的だから，ある h: P→P が存在して f=gfh となる． f は全射だから f(p)=x₀ となる p∈P が存在する．

E_n := { x∈X_n | xがfhⁿ(p)∈Gの表示に現れる }

として F₀ := E₀ ， F_n+1 := E_n+1∩f^-1(F_n) と定める．もちろん F_n⊂X_n, 0 < |F_n| < ∞ である．よって f(F_n+1)=F_n を示せばよい． f(F_n+1)⊂F_n は定義から明らか． x∈F_n とする． E_n+1={ y₀, …, y_s } と置けば fhⁿ⁺¹(p)=m₀y₀+…+m_sy_s と書ける．よって fhⁿ(p)=gfhhⁿ(p)=g(fhⁿ⁺¹(p))=m₀g(y₀)+…+m_sg(y_s) である． x∈E_n だから，ある番号 i について x=g(y_i)=f(y_i) となる．故に y_i∈E_n+1∩f^-1(F_n)=F_n+1 であり， x∈f(F_n+1) となる．

系 EP(Ab)⇒ Urysohnの補題

証明 DMC ⇒ Urysohnだからである．Urysohnの補題を参照．