定理 k を体とするとき，
選択公理
⇔ 任意の k -線型空間 V とその部分空間 A に対し， A の補空間 B が存在する．
(即ち， A⊕B=V となる B ．)

証明 (⇒) X := { W⊂V | W は部分空間， A∩W=0 } にZornの補題を適用すればよい．

( ⇐ ) 選択公理と同値なAMCを示す．

{ X_λ }_λ∈Λ を互いに素な非空集合， X := ∪_λ∈ΛX_λ とする．集合 Y に対して k^(Y) で Y を基底とする k-線型空間を表す．各 λ∈Λ に対し

A_λ := { Σ_x∈Xλa(x)x∈k^(X_λ) | Σ_x∈Xλa(x)=0 }

と定義する． A := ⊕_λ∈ΛA_λ⊂ ⊕_λ∈Λk^(X_λ) = k^(X) に仮定を適用すると A⊕B = k^(X) となる部分空間 B⊂k^(X) が存在する．

x∈X_λ を x∈k^(X) とみなして x = a(x)+b(x) (a(x)∈A, b(x)∈B) と表す．任意の x, y∈X_λ をとる． x-y∈A に注意すると

b(x)-b(y) = (x-a(x))-(y-a(y)) = (x-y)-a(x)+a(y)∈A

となるから b(x)-b(y)∈A∩B = 0 ，即ち b(x) = b(y) である．従って， b_λ := b(x) は x∈X_λ の取り方によらず λ のみから定まる． b_λ∈B⊂k^(X) なので， b_λ = Σ_y∈Xα_λ(y)y と一意に表せる．そこで F_λ := { y∈X_λ | α_λ(y)≠0 } と置く． Σ_y∈Xα_λ(y)y は実質有限和だから F_λ も有限集合である．また， x∈X_λ に対し

x-Σ_y∈Xα_λ(y)y = x-b_λ = x-b(x) = a(x)∈A = ⊕_λ∈ΛA_λ

であるが， x-Σ_y∈Xα_λ(y)y の A_λ 成分は明らかに x-Σ_y∈Xλα_λ(y)y である． A_λ の定義より 1-Σ_y∈Xλα_λ(y) = 0 ，故に α_λ(y)≠0 となる y∈X_λ は存在する．即ち F_λ は空でない．以上によりAMCが成立する．

定理 次の命題は( ZF 上)同値．

1. 選択公理
2. 0 でない線型空間の族 { V_λ }_λ∈Λ に対して，空でない有限集合の族 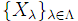で各 X_λ は一次独立な部分集合 X_λ⊂V_λ となるものが存在する．(Vector Space Multiple Choice)
3. 0 でない線型空間の族 { V_λ }_λ∈Λ に対して，非空集合の族 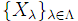で各 X_λ は一次独立な部分集合 X_λ⊂V_λ となるものが存在する．(Vector Space Kinna-Wagner Principle)

証明 1⇒2 と 2⇒3 は明らか．

(3 ⇒ 1) AMCを示す． を互いに素な非空集合の族とする．

K_λ := { f∈Q(X_λ) | f は 0 次の斉次式 }⊂Q(X_λ)

は部分体である． Q(X_λ) を K_λ 上の線型空間と見なし， X_λ で生成される部分空間を V_λ⊂Q(X_λ) とする． dim V_λ = 1 である．

仮定3を { V_λ } _λ∈Λ に適用して { Y_λ } _λ∈Λ を得る． Y_λ⊂V_λ は 0 でない一次独立な集合で， dim V_λ = 1 だったから Y_λ = { v_λ } と書ける．このとき

F_λ := { x∈X_λ | x は v_λ∈Q(X_λ) の表示に現れる }

と置けばよい．