関数解析学の定理
ZFでは証明できない関数解析学の定理としてHahn-Banachの定理が有名である. Hahn-Banachの定理はある種の写像の延長の存在を保証する定理だが, 実はHahn-Banachの定理に「延長に関する条件」を付け加えると,選択公理と同値になることが知られている.
定義Xを実線型空間とする.
- S⊂Xが凸集合
⇔ 任意の二点u, v∈Sに対し { tu+(1-t)v | t∈[0, 1] }⊂ S - S⊂Xを凸集合とする.x∈Sがextreme point
⇔ 任意の二点u, v∈Sに対し x ∉ { tu+(1-t)v | t∈(0, 1) } p: V→Rが劣線型汎関数(sublinear functional)
⇔ 任意のv, w∈Vと任意の実数ξ≧0に対し
p(v+w)≦p(v)+p(w), p(ξ v)=ξp(v)このときp(0)=p(0v)=0p(v)=0であり,
0=p(0)=p(v+(-v))≦p(v)+p(-v)
だから-p(-v)≦p(v)である.
定義 Xを集合とし,f, g: X→Rを部分関数とする(定義域をdomで表す). S⊂Xを部分集合とするとき
f≦Sg ⇔ S⊂dom(f)∩dom(g)かつ任意のx∈Sに対しf(x)≦g(x)
f=Sg ⇔ S⊂dom(f)∩dom(g)かつ任意のx∈Sに対しf(x)=g(x)
と定義する.f=Sg ⇔ f≦Sgかつg≦Sf である.
定義 Xを実線型空間,p, f: X→Rを部分関数とする. 更にpは劣線型,fは線型で,f≦dom(f)pを満たすとする.このとき
Z(p, f) := { g: dom(p)→R:線型汎関数 | g=dom(f)f, g≦dom(p)p }
と書く.明らかにZ(p, f)は凸集合である.
Hahn-Banachの定理 選択公理を仮定する. Vを実線型空間,W⊂Vを部分空間として,p: V→Rを劣線型汎関数とする. f: W→Rを線型汎関数とし,f≦Wpを満たすとする. このときZ(p, f)≠∅である.
証明A := {φ: V→R:部分線型汎関数 | W⊂dom(φ), φ≦dom(φ)p, φ=Wf} と置き,Aに順序を包含関係⊂で定める. C⊂Aを全順序部分集合とすると,φ := ∪_{ψ∈C}ψ∈Aは明らかにCの上界である. 故に(A, ⊂)にZornの補題を適用できて,極大元φ∈Aを得る. φの極大性によりdom(φ)=Vである.故にφ∈Z(p, f)である.
Hahn-Banachの定理の証明は選択公理よりも真に弱いBPI(=Boolean Prime Ideal theorem)があれば可能である.Hahn-Banachの定理を参照.
定理1
選択公理
⇔ Vを実線型空間,W⊂Vを部分空間,S⊂Vを部分集合とする.
p: V→Rを劣線型汎関数とし,線型汎関数f: W→Rはf≦Wpを満たすとする.このとき前順序集合(Z(p, f), ≦S)の極大元が存在する.
即ちあるg∈Z(p, f)が存在して,任意のh∈Z(p, f)に対し「g≦Shならばg=Sh」が成り立つ.
証明(⇒) Hahn-Banachの定理によりZ(p, f)≠∅であるから,S⊂Wのときは明らか. S⊂Wでないとする. U⊂VをWとSで生成される部分空間とする.
A := { (M, φ) | W⊂M⊂Uは部分空間, MはWとM∩Sで生成される, φは(Z(p|M, f), ≦M∩S)の極大元}
に順序関係≦を
(M, φ)≦(N, ψ) ⇔ M⊂N, φ=Mψ
で定める.C⊂Aを全順序部分集合とする. φ:=∪_{(N, ψ)∈ C}ψ,M := dom(φ)と定める. 明らかにφ∈Z(p|M, f)である. g∈Z(p|M, f)がφ≦M∩Sgを満たすとする. 任意のs∈M∩Sを取る.Mの定義よりある(N, ψ)∈Cが存在してs∈Nとなる. (N, ψ)∈C⊂Aだから,ψは(Z(p|N, f), ≦N∩S)の極大元. g|N∈Z(p|N, f), ψ≦N∩Sgだから,ψの極大性により ψ(s)=g(s)である.即ちφ(s)=g(s), 従ってφ=M∩Sgが分かり, φ∈ Z(p|M, f)は極大元である. 故に(M, φ)∈A.よって明らかに(M, φ)はCの上界である. そこで(A, ≦)にZornの補題を適用して極大元(M, φ)∈Aを得る. 極大性よりM=Uである. このときHahn-Banachの定理によりg∈Z(p, φ)⊂Z(p, f)を取れば, このgが(Z(p, f), ≦S)の極大元である.
(←)選択公理と同値なAMCを示す.
AMC (= the Axiom of Multiple Choice)とは次の命題のこと.
空でない集合の族![]() に対し,空でない有限集合の族
に対し,空でない有限集合の族![]() で∀λ∈Λ,
で∀λ∈Λ, ![]() を満たすものが存在する.
を満たすものが存在する.
同値性の証明はthe Axiom of Multiple Choiceを参照.
![]() を互いに素な非空集合の族とする.
を互いに素な非空集合の族とする.
![]() として
として
V := {φ∈R^X | 有限個のλ∈Λを除いてφ(Xλ)=0}
と定める.Vは実線型空間である.A⊂Xに対しchAでAの特性関数を表す.即ち
x∈Aのとき chA(x) := 1
x∉Aのとき chA(x) := 0
特にx∈Xに対し chx := ch{x} と書く. S := {chx|x∈X}⊂V, Sλ := {chx| x∈Xλ}⊂Vと定める. v∈Vに対し,v+(x) := max{v(x), 0}と定義して
p(v) := Σ_{λ∈Λ}sup_{x∈Xλ}v+(x)
と定めるとp: V→Rは劣線型汎関数である.f:=0: 0→Rを線型汎関数として,仮定を適用し極大元g∈(Z(p, f), ≦S)を得る. このとき
ρλ := (1/2)sup_{x∈Xλ}g(chx)
Fλ := { x∈Xλ | g(chx)>ρλ }
と定める.
λ∈Λを取る.Fλ=∅と仮定すると,g=Sλ0でなければならない.
ρλ>0と仮定すると,supの性質によりあるx∈Xλが存在してg(chx)>ρである. 故にFλ=∅に矛盾する.従ってρλ≦0となる. 即ちg≦Sλ0. pの定義より,明らかに0≦Vp.故に0∈Z(p, f)である. よってgの極大性によりg=Sλ0である.
以下,簡単のため ch = chXλ と書く.a∈Xλを一つ取り,h: V→Rを h(v) := g((1-ch)v)+v(a) で定める.pの定義により
p(v)=p((1-ch)v)+p(chv)≧ g((1-ch)v)+v+(a)≧h(v)
だからh∈Z(p, f)である.しかしx∈Xに対し
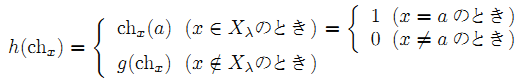
であるからg≦Shかつg≠Shとなり,gの極大性に矛盾する. 故にFλ≠∅である.またρ>0である.
|Fλ|=∞と仮定する.自然数nをnρ>1となるように決める. このときFλから互いに異なるn個の元a1, …, an∈ Fλが取れる.すると
1=p(ch{a_1, …, a_n})≧ g(ch{a_1, …, a_n}) =g(cha_1)+… +g(cha_n)≧nρ>1
となり矛盾する.故に|Fλ|<∞となる.
以上よりAMCが示された.
定理2 以下の命題は(ZF上)同値
- 選択公理
- Vを実線型空間,W⊂Vを部分空間として,p: V→Rを劣線型汎関数とする. f: W→Rを線型汎関数とし,f≦Wpを満たすとする. このときZ(p, f)はextreme pointを持つ.
- 「実ノルム空間の双対空間」の単位球体はextreme pointを持つ
証明(1 ⇒ 2) 整列可能定理を使ってV\Wを整列し,順序数λを使ってV\W = { vα| α<λ } と書く. α<λに対し(qα, Kα, pα)を以下の性質(a)~(e)を満たすように超限帰納法で定義する.
(a) pα, qα: V→Rは劣線型汎関数である.
(b) f≦Wpα
(c) pα(v)≧-p0(-v)
(d) β<αのときpβ≧Vpα
(e) Kα=Z(pα, f)
(i) α=0のとき.
q0 := p
K0 := { g∈Z(q0, f) | gは(Z(q0, f), ≦{v0})の極大元}
p0(v) := sup{ g(v) | g∈K0 } (v∈V)
と定める.この定義が可能なこと,またこれらが性質(a)から(e)を満たすことを確認する. q0が劣線型であることは良い.勿論 f ≦W q0である. 故に定理1により K0 ≠ ∅ である. g∈K0(⊂Z(q0, f)) のとき g ≦V q0だから, 各v∈Vについて { g(v) | g∈K0 } は上に有界である. 故にp0(v)=sup{ g(v) | g∈K0 } は定義され, 特にp0≦Vq0となる. p0, K0の定義から明らかに
(f) 任意のg∈K0に対しg(v0)=p0(v0)
となる.また,任意のv, w∈ V, ξ≧0に対し
p0(v+w)
=sup{ g(v+w) | g∈K0 }
=sup{ g(v)+g(w) | g∈K0 }
≦sup{ g(v) | g∈K0 } + sup{ g(w) | g∈K0 }
=p0(v)+p0(w)
p0(ξv)
=sup{ g(ξv) | g∈K0 }
=sup{ ξg(v) | g∈K0 }
=ξp0(v)
だから,p0: V→Rは劣線型汎関数である. 故に(c) p0(v)≧-p0(-v)が成り立つ. またp0の定義より f ≦W p0 だからZ(p0, f)を考えることができる. このとき(e) K0=Z(p0, f)が分かる.
p0の定義より,任意のg∈K0に対し g ≦V p0 だから,K0⊂Z(p0, f) は明らか. 逆を示すため,g∈Z(p0, f)を取る. p0 ≦V q0 だったからg∈Z(q0, f)である.また
-p0(-v0)
=-sup{ h(-v0) | h∈K0 }
=inf{ h(v0) | h∈K0 }
=inf{ p0(v0) | h∈K0 } (∵ (f)より)
=p0(v0).
g≦Vp0だからg(v0)≦p0(v0)であり,かつ
g(v0) = -g(-v0)≧-p0(-v0) = p0(v0).
故にg(v0)=p0(v0)となる.よってg∈K0が分かる.
以上よりα=0の時は(a)から(e)が成り立つことが分かった.
(ii) 0<α<λのとき.
qα(v) := inf{ pβ(v) | β<α } (v∈ V)
Kα := { g∈Z(qα, f) | gは (Z(qα, f), ≦{vα})の極大元 }
pα(v) := sup{ g(v) | g∈Kα } (v∈V)
と置く.この定義が可能なこと,またこれらが性質(a)から(e)を満たすことを確認する. 帰納法の仮定(c)よりβ<αに対しpβ(v)≧-p0(-v)だから, {pβ(v)|β<α}は下に有界である. 故にqα(v)=inf{ pβ(v) | β<α } は定義される. 任意のv, w∈V, ξ≧0に対し
qα(v+w)
=inf{ pβ(v+w) | β<α }
≦inf{ pβ(v)+pβ(w) | β<α } (∵帰納法の仮定(a))
=inf{ pβ(v) | β<α } + inf{ pβ(w) | β<α } (∵帰納法の仮定(d))
=qα(v)+qα(w).
qα(ξv)
=inf{ pβ(ξv) | β<α }
=inf{ ξpβ(v) | β<α } (∵帰納法の仮定(a))
=ξqα(v).
即ちqα: V→Rは劣線型汎関数である. 帰納法の仮定(b)により qα(v)=inf{ pβ(v) | β<α }≧f(v)だから f≦Wqαである. 故に定理1によりKα≠∅である. g∈Kα(⊂Z(qα, f))のときg≦qαだから, { g(v) | g∈Kα } は上に有界である. よって pα(v)=sup{ g(v) | g∈Kα} は定義され, 特にpα≦Vqαである.従ってβ<αに対し pα(v)≦qα(v)=inf{ pβ(v) | β<α }≦ pβ(v), 即ち(d)が成り立つ. 特にpα(-v)≦p0(-v)であるから, pα(v)≧-pα(-v)≧-p0(-v),即ち(c)が成り立つ. pα, Kαの定義から明らかに
(g) 任意の g∈Kα に対し g(vα)=pα(vα)
となる.また,任意のv, w∈V, ξ≧0に対し
pα(v+w)
=sup{ g(v+w) | g∈Kα }
=sup{ (g(v)+g(w)) | g∈Kα }
≦sup{ g(v) | g∈Kα } + sup{ g(w) | g∈Kα }
=pα(v)+pα(w).
pα(ξ v)
=sup{ g(ξv) | g∈Kα}
=sup{ ξg(v) | g∈Kα}
=ξpα(v).
従ってpα: V→Rは劣線型汎関数である. またpαの定義より f ≦W pα だからZ(pα, f)を考えることができる.このとき(e) Kα=Z(pα, f)が成り立つ.
pαの定義より,任意のg∈Kαに対し g ≦V pαだから, Kα⊂Z(pα, f) は明らか. 逆を示すため,g∈Z(pα, f) を取る. pα ≦V qα だったから g∈Z(qα, f) である.また
-pα(-vα)
=-sup{ h(-vα) | h∈Kα }
=inf{ h(vα) | h∈Kα }
=inf{ pα(vα) | h∈Kα } (∵ (g)より)
=pα(vα).
g≦Vpαだったからg(vα)≦pα(vα)であり,かつ
g(vα)=-g(-vα)≧-pα(-vα)=pα(vα).
故にg(vα)=pα(vα)でなければならない. よってg∈Kαが分かる.
さて,v∈Vに対しqλ(v):=inf{ pα(v) | α<λ } と定める. 明らかに,α<λに対しpα≧Vpλである. 性質(b)によりf≦Wqλであるから, Hahn-Banachの定理によりZ(qλ, f)≠∅である. 0<α≦λとする.このときZ(qα, f)=∩β<α Kβとなる.
任意のβ<αを取ると,qα≦V pβだから Z(qα, f)⊂Z(pβ, f)=Kβ. 故にZ(qα, f)⊂∩β<α Kβである.
逆にg∈∩β<α Kβとする.任意のβ<αに対し g∈ Kβ=Z(pβ, f)だからg≦Vpβである. よってg(v)≦inf{ pβ(v) | β<α }=qα(v)となり, g∈Z(qα, f)である.
φ, ψ∈Z(qλ, f)とする. α<λとするとφ, ψ∈Kαだから φ(vα) = pα(vα) = ψ(vα) である. 故にφ=Vψである.即ちZ(qλ, f)={φ}と書ける. このφがextreme pointである.
あるg, h∈Z(p, f), g, h≠φと 0<t<1 を使ってφ=tg+(1-t)h と書けたと仮定する. γ := min{ α<λ | g ∉ Kα または h ∉ Kα } と置く. φ∈K0だからp0(v0)=φ(v0)=tg(v0)+(1-t)h(v0)となる. g(v0), h(v0)≦p0(v0)であるから, g(v0) = h(v0) = p0(v0) でなければならない. 故にg, h∈ K0だから,γ>0である. g, h∈∩α<γ Kα=Z(qγ, f)だから g, h≦qγ となる. 「g ∉ Kγ または h ∉ Kγ」だから, 「g(vγ)<pγ(vγ)またはh(xγ)<pγ(vγ)」である.どちらにしてもφ(vγ)=tg(vγ)+(1-t)h(vγ)<pγ(vγ)となり,φ∈Z(qλ, f)⊂ Kγに矛盾する.
(2 ⇒ 3) (V, ||・||V)を実ノルム空間とする. ||・||V: V→Rは劣線型写像である. そこで W := 0, f := 0:0→Rとして仮定2を使えば Z(||・||V, f)⊂V*はextreme pointを持つ. S⊂V*を単位球体とする. 即ちS := { g∈V* | ||g||V*≦1 } であるが, || g||V*≦1 ⇔ |g(・)| ≦V ||・||Vである. 故にZ(||・||V, f)=Sとなり,Sはextreme pointを持つ.
(3 ⇒ 1)
![]() を非空集合の族とする.Xλは互いに素としてよい.
X :=
を非空集合の族とする.Xλは互いに素としてよい.
X := ![]() として
として
V := { f∈R^X | 任意のε>0に対し{ x∈X | |f(x)|>ε } は有限集合,
Σλ∈Λ sup{ |f(x)| | x∈Xλ }<∞ }
W := { g∈R^X | sup{ Σx∈Xλ |g(x)| | λ∈Λ }<∞ }
と定める.これらは次のノルムでノルム空間になる.
||f||V := Σ_{λ∈Λ}sup{ |f(x)| | x∈Xλ }
||g||W := sup{ Σ_{x∈Xλ}|g(x)| | λ∈Λ }
S := { g∈W | ||g||W≦1 }⊂W を単位球体とする. V* := { ξ: V→R:有界線型 } をVの双対空間とすると, 後で述べる補題により等長同型 W ≅ V*が成り立つ.
これによりSをV*内の単位球体とみなす.仮定よりSは extreme point e∈S を持つ.任意のλ∈Λを取る.e(x)≠0となるx∈ Xλが一意に存在する.
まず存在を示す.その為に,全てのx∈Xλについてe(x)=0であると仮定する. u∈Xλを一つ取り,x∈Xに対し
f(u) := 1
x≠uのとき f(x) := e(x)
g(u) := -1
x≠uのとき g(x) := e(x)
と定めるとf, g∈Sであり,これらはf≠e, g≠e, e=(f+g)/2 を満たす.即ちeがextreme pointであることに矛盾する.故にe(x)≠0となるx∈Xλは存在する.
次に一意性を示す.その為に,u, v∈Xλ, u≠vがe(u), e(v)≠0を満たすと仮定する.
f(u) := e(u)(1+|e(v)|)
f(v) := e(v)(1-|e(u)|)
x≠u, vのとき f(x) := e(x)
g(u) := e(u)(1-|e(v)|)
g(v) := e(v)(1+|e(u)|)
x≠u, vのとき g(x) := e(x)
と定めるとf, g∈Sであり,これらはf≠e, g≠e, e=(f+g)/2 を満たす.即ちeがextreme pointであることに矛盾する.故にe(x)≠0となるx∈ Xλは一意的である.
そこで F: Λ→ X=∪XλをF(λ) := (e(x)≠0となるx∈ Xλ) で定めればFが選択関数となる.
さて,関数解析において次のような定理がある.
Banach-Alaogluの定理 ノルム空間 X の双対空間 X* の閉単位球体 B⊂X* は弱*位相でコンパクトである.
Krein-Milmanの定理 局所凸位相線型空間のコンパクト凸集合はextreme pointを持つ.
定理 選択公理 ⇔ Banach-Alaogluの定理 + Krein-Milmanの定理
証明 ( ⇒ ) 略
( ← )前定理の条件3を示す. X を実ノルム空間とする. X* は局所凸位相線型空間で,単位球体 B⊂X* は凸集合である.Banach-Alaogluにより B⊂X* はコンパクトである.故にKlein-Milmanの定理により B はextreme pointを持つ.
補題 等長同型 W ≅ V*が成り立つ.
証明f∈V, g∈Wに対し
Σ_{λ∈Λ}(Σ_{x∈ Xλ}|g(x)||f(x)|)
≦Σ_{λ∈Λ}((sup_{y∈ Xλ}|f(y)|)Σ_{x∈ Xλ}|g(x)|)
≦(sup_{λ∈Λ}Σ_{x∈ Xλ}|g(x)|)(Σ_{λ∈Λ}sup_{y∈ Xλ}|f(y)|)
≦||g||W||f||V
故にΣ_{λ∈Λ}Σ_{x∈ Xλ}g(x)f(x)は絶対収束する.そこで
φ(g)(f):=Σ_{λ∈Λ}Σ_{x∈ Xλ}g(x)f(x)
と定義する.φ(g): f |→ φ(g)(f)はV*の元である. 故に線型写像φ: W→V*が得られる. また||φ(g)||V*≦|| g||Vも分かる.
任意のε>0を取る.||g||Wの定義とsupの性質により,あるμ∈Λが存在して Σ_{x∈ Xμ}|g(x)|>||g||W-ε/2となる. 更に,ある有限部分集合A⊂ Xμが存在して Σ_{x∈A}|g(x)|>Σ_{x∈Xμ}|g(x)|-ε/2 とできる.そこでh∈Vを
x∈Aかつg(x)>0のとき h(x) := 1
x∈Aかつg(x)<0のとき h(x) := -1
(それ以外のとき h(x) := 0
で定義すれば||h||V=1であり,
||φ(g)||V*
≧Σ_{x∈A}|g(x)|
>||g||W-ε.
故に||φ(g)||V*>||g||W-εとなる. ε>0は任意だったから,||φ(g)||V*≧||g||Wが分かる. 即ち||φ(g)||V*=||g||Wであり,φは等長写像である.
任意のξ∈ V*を取る. x∈Xに対しchx:=ch{x}∈Vを特性関数として gξ(x) := ξ(chx)と置く.gξ∈Wである.
gξ∉ Wと仮定する.gξ∈RXだから
sup_{λ∈Λ}(Σ_{x∈Xλ}|g(x)|)=∞
でなければならない.そこで任意の実数M>0を取ると,あるμ∈Λが存在して Σ_{x∈Xμ}|g(x)|>2Mとなる. 更に,ある有限部分集合A⊂Xμが存在して Σ_{x∈A}|g(x)|>Mとできる. そこでh∈Vを
x∈Aかつg(x)>0のとき h(x) := 1
x∈Aかつg(x)<0のとき h(x) := -1
それ以外のとき h(x) := 0
で定義すれば|| h||V=1であり,
|ξ(h)|
=|ξ(Σ_{x∈ A}h(x)chx)|
=|Σ_{x∈ A}h(x)ξ(chx)|
=Σ_{x∈ A}|gξ(x)|>M
となる.故に
||ξ||V*=sup_{0≠ f∈ V}\frac{|ξ(f)|}{|| f||V} ≧\frac{|ξ(h)|}{|| h||V}>M.
M>0は任意だったから||ξ||V*=∞となるが,これは ξの有界性に矛盾する.
任意のf0∈Vを取る.
任意のε>0を取ると,φ(g), ξ∈V^*は有界,即ち連続だから, あるδ>0が存在して任意のf∈Vに対し
||f-f0||V<δ⇒ |φ(g)(f)-φ(g)(f0)|<ε/2, |ξ(f)-ξ(f0)|<ε/2.
(i) n := |{ λ∈Λ | ∃x∈Xλ(f0(x)≠0) }| < ∞のとき.
{ λ∈Λ | ∃x∈Xλ(f0(x)≠0) } = {λ1, …, λn}と書く.
Vの定義より
A := { x∈X | |f(x)|≧δ/n } は有限集合となる.
そこでf∈Vとして
x∈Aのとき f(x) := f0(x)
x∉Aのとき f(x) := 0
を取れば
||f-f0||V
=Σ_{λ∈Λ}sup{ |f(x)-f0(x)| | x∈Xλ }
=Σ_{i=1}^n sup{ |f0(x)| | x∈Xλ_i\A }
<Σ_{i=1}^n δ/n
=δ.
更に
φ(gξ)(f)
=Σ_{λ∈Λ}Σ_{x∈Xλ}gξ(x)f(x)
=Σ_{x∈A}gξ(x)f(x)
=Σ_{x∈A}ξ(chx)f(x)
=ξ(Σ_{x∈A}f(x)chx)=ξ(f)
故に
|φ(gξ)(f0)-ξ(f0)|
≦|φ(gξ)(f0)-φ(gξ)(f)|+|ξ(f)-ξ(f0)|
<ε/2 + ε/2
=ε.
(ii) |{ λ∈Λ | ∃x∈Xλ(f0(x)≠0) }| = ∞のとき.
||f0||V=Σ_{λ∈Λ}sup{ |f0(x)| | x∈Xλ }だから,
ある有限部分集合Λ1⊂Λが存在して
Σ_{λ∈Λ1}sup{ |f0(x)| | x∈Xλ } >||f0||V-δ/2
となる.このときΛ2 := Λ\Λ1と置けば
Σ_{λ∈Λ2}(sup{ |f0(x) | x∈Xλ })<δ/2.
n := |Λ1| としてΛ1={λ1, …, λn}と書く. Vの定義より A := { x∈Xλ_1∪…∪Xλ_n | |f(x)|≧δ/2n } は有限集合となる. そこでf∈Vとして
x∈Aのとき f(x) := f0(x)
x∉Aのとき f(x) := 0
を取れば
||f-f0||V
=Σ_{λ∈Λ}sup{ |f(x)-f0(x)| | x∈Xλ }
=Σ_{λ∈Λ1}sup{ |f(x)-f0(x)| | x∈Xλ }
+Σ_{λ∈Λ2}sup{ |f(x)-f0(x)| | x∈Xλ }
=Σ_{λ∈Λ1}sup{ |f0(x)| | x∈Xλ\A }
+Σ_{λ∈Λ2}sup{ |f0(x)| | x∈Xλ }
<Σ_{i=1}^n δ/2n + δ/2
=δ.
更に
φ(gξ)(f)
=Σ_{λ∈Λ}Σ_{x∈Xλ}gξ(x)f(x)
=Σ_{x∈A}gξ(x)f(x)
=Σ_{x∈A}ξ(chx)f(x)
=ξ(Σ_{x∈A}f(x)chx)
=ξ(f)
故に
|φ(gξ)(f0)-ξ(f0)|
≦|φ(gξ)(f0)-φ(gξ)(f)|+|ξ(f)-ξ(f0)|
<ε/2 + ε/2
=ε.
ε>0は任意だったから,(i)(ii)により |φ(gξ)(f0)-ξ(f0)|=0,即ちφ(gξ)(f0)=ξ(f0)である.
f0∈Vは任意だったからφ(gξ)=ξが分かる.故にφ: W→V^*は全射である. 以上より等長同型 W≅V* が示された.
参考文献
- P. R. Andenaes, Hahn-Banach Extensions which are Maximal on a Given Cone, Math. Ann. 188, 90-96 (1970)
- F. F. Bonsall, Sublinear Functionals and Ideals in Partially Ordered Vector Spaces, Proc. London Math. Soc. (1954), 402-418
- J. L. Bell and D. H. Fremlin, A geometric form of the axiom of choice, Fundamenta mathematicae, 77(1973), 167-170,
- H. Rubin and J. Rubin, Equivalents of the Axiom of Choice II, North Holland, 1985.
コメント
定理1のpのdefのところで、各λに対してsup v+(x)が定まらない(有界でない)恐れがあるので、Vの定義にそれを課すべきではないでしょうか