明らかに有限集合はDedekind有限集合である(即ち，Dedekind無限集合は無限集合である)． 逆に無限集合がDedekind無限集合であることはZFでは証明できないことが知られている． つまり，ZFに命題「Dedekind有限な無限集合が存在する」を加えても(ZFが無矛盾ならば)矛盾しないのである． 一方，選択公理を仮定すれば無限集合がDedekind無限集合であることが証明できる．

まずDedekind無限集合であることの同値な条件を述べておく． 濃度に関する記号については基数の性質を参照．

命題 集合Xに対し次の条件は(ZF上)同値

1. XはDedekind無限集合．
2. 全射でない単射 X→X が存在する．
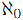3. ≦|X|
4. 単射 N→X が存在する．
5. Xは可算無限部分集合を持つ．
6. |X| = |X|+
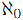
7. |X| = |X|+1

証明 1⇔2 と 3⇔4⇔5 は明らか．

(2⇒4) f: X→X を全射でない単射とする． 全射でないから x∈X＼f(X) が取れる． このとき g: N→X を

g(0) := x
n>0に対し g(n) := f(f(…f(x)…))　(fのn回合成)

で定義すればこれは単射である．

(5⇒6) Y⊂Xを可算無限部分集合とする．|Y|=|Y|+だから

|X| = |(X＼Y)∪Y| = |X＼Y|+|Y| = |X＼Y|+|Y|+ = |X|+.

(6⇒7) =+1だから

|X| = |X|+ = |X|++1 = |X|+1.

(7⇒1) Xに含まれない元∞を一つ取る．|X| = |X|+1 より 全単射 f: X∪{∞}→X が存在する． このとき f(X) ⊊ X かつ |f(X)| = |X| である．

定理選択公理を仮定する．無限集合はDedekind無限である．

証明整列可能定理を使えば明らか．

直接示すには「選択公理⇒整列可能定理」の証明を真似ればよい． Xを無限集合とする．命題により単射f: N→ Xの存在を示せばよい．選択公理によりP(X)＼{∅}の選択関数 g が存在する． このとき f: N→X を帰納的に f(n) := g(X＼{g(0), g(1), …, g(n-1)})で定義すればよい．

Xが無限集合であるから，X＼{g(0), g(1), …, g(n-1)}≠∅となることに注意する．

実は，この命題は可算選択公理があれば証明できる．

定理可算選択公理を仮定する．無限集合はDedekind無限である．

証明Xを無限集合とする．命題により可算無限部分集合Y⊂Xの存在を示せばよい．非負整数 n に対し X_n := { <x₀, x₁, …, x_n>∈Xⁿ⁺¹ | i≠j ならば x_i≠x_j } と置く． X が無限集合だから X_n≠∅ である． そこで集合族{X_n}_n∈Nに可算選択公理を適用して選択関数φ : N→∪_n∈NX_nを得る．φ(n)∈X_n⊂Xⁿだからφ(n)=<x₀⁽ⁿ⁾, x₁⁽ⁿ⁾, …, x_n⁽ⁿ⁾>と書ける． Y := { x_i⁽ⁿ⁾ | i≦n } と置けば， A := {<i, n>∈N×N | i≦n } は可算無限集合だから Y は高々可算集合である．しかし X_n の定義から明らかに Y は無限集合である． 従って Y⊂X は可算無限部分集合である．

定理任意の無限集合Xに対し |X|+|X| = |X|
⇒無限集合はDedekind無限集合

証明Xを無限集合とすると仮定より全単射 f: ({0}×X)∪({1}×X)→X が存在する． このとき明らかに f({0}×X) ⊊ X かつ |f({0}×X)| = |X| である．

定理 |X|<|Y| かつ |Y|≦*|X| となるような無限集合X, Yは存在しない
⇒無限集合はDedekind無限集合

証明AをDedekind有限な無限集合とする． A_n := { <a₀, a₁, …, a_n>∈Aⁿ⁺¹ | i≠jならばx_i≠x_j } と置いて X := ∪_n∈NA_n, Y := X∪{∅} と置く． 明らかに |X|≦|Y|, |Y|≦*|X| である． 従って |X|≠|Y| を示せばよい．

AがDedekind有限であることからYもDedekind有限集合である． 明らかに |Y| = |X|+1 で，また命題により |Y|≠|Y|+1 である． よって |X|≠|Y| である．

最後に，命題「無限集合はDedekind無限集合である」と同値な命題を述べておく．その為にまず補題を一つ示す．

補題 Xを集合とする．このとき

≦* |X|⇔≦P(X)

証明(⇒) f: X→Nを全射とする．このとき f^-1: N→P(X)は単射である．

(←) f: N→P(X) を単射とする． g: N→P(X) を以下のように帰納的に定義する．

nを非負整数とする．0≦m≦n-1に対しg(m)が

| { f(k)＼∪_m<ng(m) | k≧n } | = ∞

となるように定義されているとする． このとき

n^* := min{ k∈N | k≧n, f(k)＼∪_m<ng(m)≠∅, (X＼f(k))＼∪_m<ng(m)≠∅ }

として

( | { f(k)＼(f(n^*)∪∪_m<ng(m)) | k>n^* } | = ∞ のとき
g(n) := f(n^*)＼∪_m<ng(m)
それ以外のとき
g(n) := X＼(f( n^*)＼∪_m<ng(m) )

と定める．

このとき h: X→N を

x∈g(n) のとき　h(x) := n
x∈X＼∪_m∈Ng(m) のとき　h(x) := 0

と定めればhは全射である．

定理次の命題は(ZF上)同値．

1. 任意の無限集合はDedekind無限集合である．
2. Dedekind有限集合からNへの全射は存在しない．
3. Dedekind有限集合の冪集合はDedekind有限集合である．
4. Dedekind有限集合 X とDedekind無限集合 Y に対し |X|≦ |Y|．
5. 非可算集合 X と可算集合 Y に対し |X∪Y| = |X|．
6. 非可算集合 X と可算集合 Y に対し |X＼Y| = |X|．
7. |X|> 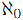かつ |Y|= 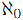ならば |X＼Y|>．
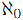8. 任意の集合 X に対し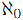≦|X| または |X|≦．

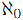証明(1⇒2) 仮定1よりDedekind有限集合は有限集合だから明らか．

(2⇒3) XをDedekind有限集合とする． 仮定2により ￢≦*|X| だから 補題により ￢≦P(X) となる． 即ち P(X) はDedekind有限集合である．

(3⇒1) Dedekind有限な無限集合 X が存在すると仮定する． Xが無限集合だから P(X)∋Y |→ |Y|∈N は全射である． 即ち≦*|P(X)|． 従って補題により P(P(X)) はDedekind無限集合である． 一方 X がDedekind有限だから仮定3により P(P(X)) がDedekind有限集合となり矛盾する．

(1⇒4) 仮定1よりDedekind有限集合は有限集合だから明らか．

(4⇒1) XをDedekind有限集合とする． NはDedekind無限集合だから仮定4により |X|≦． よって X が無限集合と仮定すると X は可算無限，即ちDedekind無限集合となって矛盾する．

(1⇒5) X を非可算集合，Y を可算集合とする．仮定より X はDedekind無限集合である． |Y＼X|≦だから 命題の条件6と7により

|X∪Y| = |X|+|Y＼X| = |X|.

(5⇒6) X を非可算集合，Y を可算集合とすると X＼Y も非可算集合である． 故に仮定5により |X| = |(X＼Y)∪Y| = |X＼Y|．

(6⇒7) 明らか．

(7⇒1) Xを無限集合とする．X が可算無限ならば明らかにDedekind無限だから，X は非可算無限集合としてよい． 更にX∩N = ∅ としても一般性を失わない． このとき |X∪N|>だから仮定7により |X| = |(X∪N)＼N| > ． 故に X はDedekind無限集合である．

(1⇔8) 明らか．