濃度の性質
以下の命題の証明は順序数・濃度の簡単なまとめを参照.
命題1
任意の濃度 κ, λ について
κ≦λ ⇔ ある濃度 μ が存在して κ+μ= λ
命題2 濃度 κ, λ≧2 に対し κ+λ≦κ・λ .
命題3
![]() 0≦κ ならば 2κ-κ=2κ .
0≦κ ならば 2κ-κ=2κ .
命題4
任意のアレフ ![]() に対して
に対して ![]() 2=
2=![]() .
.
命題5
任意のアレフ ![]() ,
, ![]() ' に対し
' に対し ![]() ・
・![]() '=
'=![]() +
+![]() '=max {
'=max { ![]() ,
, ![]() ' } .
' } .
命題6
濃度 κ, λ, μ とアレフ ![]() が κ・
が κ・![]() ≦λ+μ を満たすとき, κ≦λまたは
≦λ+μ を満たすとき, κ≦λまたは ![]() ≦μ.
≦μ.
命題7
濃度 κ, λ, μ とアレフ ![]() が κ・λ≦
が κ・λ≦![]() +μ を満たすとき, κ≦
+μ を満たすとき, κ≦![]() または λ≦μ .
または λ≦μ .
命題8
濃度 κ, λ とアレフ ![]() が
が ![]() ≦κ・λ を満たすとき,
≦κ・λ を満たすとき, ![]() ≦κ または
≦κ または ![]() ≦λ である.
≦λ である.
命題9 Pfin(X) := { Y⊂X | Y は有限集合 } と置くと,整列可能な無限集合 X に対し |X|=|Pfin(X)| .
命題10 Γ(X):= { α|α は順序数, |α|≦|X| } と置く.この Γ をHartogs関数という.また κ=|X| のとき κ*:=|Γ(X)| と書く.これをHartogs numberという.Hartogs numberはアレフである.
- Γ(X) は |α|
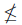 |X| となるような順序数 α のうち最小の順序数である.
|X| となるような順序数 α のうち最小の順序数である. - κ* は

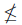 κ となるようなアレフ
κ となるようなアレフ  のうち最小のアレフである.
のうち最小のアレフである. - κ*≦22κ2
- κ*≦222κ
- 無限濃度 κ に対して κ**=(κ+κ*)*
- 無限濃度 κ に対して (κ2)*=κ*
定理11
κ, λ, μ, ν は無限濃度, ![]() はアレフを表すとする.次の命題は( ZF 上)同値.
はアレフを表すとする.次の命題は( ZF 上)同値.
- 選択公理
- 任意の κ に対しある
 が存在して κ≦
が存在して κ≦ .
. - κ≦κ* .
- κ・κ*=κ+κ* .
- κ・λ=κ+λ .
- κ2=κ .
- κ+κ*=κ* .
- κ+λ=κ または κ+λ=λ .
- κ・κ*=κ* .
- κ・λ=κ または κ・λ=λ .
- 任意の κ に対しある λ が存在して κ=λ2 .
- κ2 =λ2 ならば κ=λ .
- κ < λ かつ μ < ν ならば κ+μ < λ+ν .
- κ < λ かつ μ < ν ならば κ・μ < λ・ν .
- κ+μ < λ+μ ならば κ < λ .
- κ・μ < λ・μ ならば κ < λ .
- κ < λ ならば λ-κ が存在する.
- κ < λ ならば λ-κ=λ .
- κ < λ ならばある μ が存在して λ=κ・μ
- κ < λ ならば λ÷κ が存在する.
- κ < λ ならば λ÷κ=λ .
- κ+μ=κ+ν ならば μ=ν または μ, ν < κ .
- κ+κ < κ+λ ならば κ < λ .
- μ < κ かつ ν < κ ならば μ+ν≠κ .
- μ < κ かつ ν < κ ならば μ・ν≠κ .
- μκ < μλ かつ μ≠0 ならば κ < λ .
- κ*=μ*⇒κ=μ .
- κ* < μ < κ+κ* となる μ は存在しない.
- κ* < μ*⇒κ < μ .
- κ* <
 *⇒κ <
*⇒κ <  .
. - κ < μ⇒κ* < μ* .
-
 < μ⇒
< μ⇒ * < μ* .
* < μ* . - κ* < κ*+κ⇒κ**≦κ*+κ .
- κ≦λ+μ ならば κ≦λ または κ≦μ .
- κ≦λ+
 ならば κ≦λ または κ≦
ならば κ≦λ または κ≦ .
. - κ≦λ・μ ならば κ≦λ または κ≦μ .
- κ≦λ・
 ならば κ≦λ または κ≦
ならば κ≦λ または κ≦ .
.
証明 (1 ⇒ その他)整列可能定理により,全ての無限濃度はアレフである.よって命題4等から容易に2-37が従う.(26は濃度の比較可能性により対偶が「 κ≧λ ならば μκ≧μλ または μ= 0 」なので成り立つ.)
(2 ⇒ 1)明らか.
(3 ⇒ 2) κ* がアレフであるから明らか.
(4 ⇒ 3) κ・κ*=κ+κ* とすると, κ* はアレフだから命題6より κ≦κ* または κ*≦κ である. κ*![]() κ だから κ≦κ* となる.
κ だから κ≦κ* となる.
(5 ⇒ 4)明らか.
(6 ⇒ 5) κ+λ=(κ+λ)2=κ2+2・κ・λ+λ2≧κ・λ≧κ+λ .
7 ⇒ 3は明らか.
(8 ⇒ 7) κ+κ*=κ と仮定すると κ*≦κ となり矛盾する.故に仮定8より κ+κ*=κ* である.
(9 ⇒ 3)明らか.
(10 ⇒ 9) κ・κ*=κ と仮定すると κ*≦κ となり矛盾する.故に仮定10より κ・κ*=κ* である.
(11 ⇒ 7)仮定11より, κ+κ*=λ2 となる λ が存在する. κ*≦κ+κ*=λ2 である.よって命題8より κ*≦λ となる.従って命題1により λ=κ*+μ となる μ が取れる.このとき
κ+κ*=λ2=(κ*+μ)2=(κ*)2+2・κ*・μ+μ2≧κ*・μ.
よって命題6から κ*≦κ または μ≦κ* が分かる. κ*![]() κ なので μ≦κ* ,従って λ=κ*+μ≦κ*+κ*=κ* ,故に λ=κ* である.よって κ+κ*=λ2=(κ*)2=κ* である.
κ なので μ≦κ* ,従って λ=κ*+μ≦κ*+κ*=κ* ,故に λ=κ* である.よって κ+κ*=λ2=(κ*)2=κ* である.
(12 ⇒ 3) λ:=κ![]() 0 と置くと κ≦λ かつ λ2=κ2・
0 と置くと κ≦λ かつ λ2=κ2・![]() 0=κ
0=κ![]() 0=λ である. (λ+λ*)2=λ2+2・λ・λ*+(λ*)2≧λ・λ* となるが,一方
0=λ である. (λ+λ*)2=λ2+2・λ・λ*+(λ*)2≧λ・λ* となるが,一方
(λ+λ*)2
= λ2+2・λ・λ*+(λ*)2
= λ+2・λ・λ*+λ*
≦λ・λ*+2・λ・λ* (命題2より)
= λ・(3・λ*)
= λ・λ*
だから, (λ+λ*)2=λ・λ* となる.よって (λ+λ*)2=λ・λ*=λ2・(λ*)2=(λ・λ*)2 が成り立つ.従って仮定12より λ+λ*=λ・λ* である.故に命題6から κ≦λ≦λ* が分かる.
(13 ⇒ 2) λ:=![]() 0・κ と置くと κ≦λ かつ 2・λ=2・
0・κ と置くと κ≦λ かつ 2・λ=2・![]() 0・κ=
0・κ=![]() 0・κ=λ である. λ < λ+λ* かつ λ* < λ+λ* と仮定すると仮定13より λ+λ* < (λ+λ*)+(λ+λ*)=2・λ+2・λ* =λ+λ* となって矛盾する.故に λ=λ+λ* または λ*=λ+λ* である. λ*
0・κ=λ である. λ < λ+λ* かつ λ* < λ+λ* と仮定すると仮定13より λ+λ* < (λ+λ*)+(λ+λ*)=2・λ+2・λ* =λ+λ* となって矛盾する.故に λ=λ+λ* または λ*=λ+λ* である. λ*![]() λ なので λ* =λ+λ* でなければならない.即ち κ≦λ≦λ* である.
λ なので λ* =λ+λ* でなければならない.即ち κ≦λ≦λ* である.
(14 ⇒ 2) λ:=κ![]() 0 として13 ⇒ 2と同様にすればよい.
0 として13 ⇒ 2と同様にすればよい.
(15 ⇒ 7) κ* < κ+κ* と仮定すると κ*+κ*=κ* < κ+κ* だから仮定15より κ* < κ となり矛盾する.
(16 ⇒ 9)15 ⇒ 7と同様.
(17 ⇒ 7) κ* < κ+κ* と仮定する.仮定17より κ+κ* =κ* +μ となる μ が唯一つ存在する. μ=κ も μ=κ+κ* もこの式を満たすから,一意性より κ=κ+κ* .従って κ*≦κ となり矛盾.
(18 ⇒ 17)明らか.
(19 ⇒ 7) κ* < κ+κ* と仮定する.仮定19より κ+κ*=κ*・μ となる μ が存在する.従って命題6より κ*≦κ または μ≦κ* である. κ*![]() κ だったから μ≦κ* である.よって命題5より κ+κ*=κ*・μ=κ* となり矛盾する.故に κ*=κ+κ* である.
κ だったから μ≦κ* である.よって命題5より κ+κ*=κ*・μ=κ* となり矛盾する.故に κ*=κ+κ* である.
20 ⇒ 19と21 ⇒ 20は明らか.
(22 ⇒ 3) κ*+κ=κ*+(κ+κ*) だから仮定22より κ=κ+κ* または κ, κ+κ* < κ* である. κ*![]() κ だから κ, κ+κ* < κ* となる.従って κ≦κ* である.
κ だから κ, κ+κ* < κ* となる.従って κ≦κ* である.
(23 ⇒ 7) κ*+κ*=κ*≦κ*+κ である. κ*+κ* < κ*+κ だとすると仮定23から κ* < κ となり矛盾するので κ*=κ*+κ である.
(24 ⇒ 18) κ < λ とする.命題1より λ=κ+μ となる μ が存在する.仮定24より λ=μ となる,即ち μ は一意に決まる.よって λ-κ=λ である.
(25 ⇒ 9) κ≦κ・κ*, κ*≦κ・κ* なので,仮定25より κ=κ・κ* または κ*=κ・κ* である. κ*![]() κ だったから κ*=κ・κ* となる.
κ だったから κ*=κ・κ* となる.
(26 ⇒ 2) μ:=2κ![]() 0 と置く. μκ=(2κ
0 と置く. μκ=(2κ![]() 0)κ=2κ
0)κ=2κ![]() 0+1=2κ
0+1=2κ![]() 0=μ≦μμ* である. μκ=μμ* だとすると μ*≦μμ*=μκ=μ となり矛盾するから, μκ < μμ* である.故に仮定26より κ < μ* である.
0=μ≦μμ* である. μκ=μμ* だとすると μ*≦μμ*=μκ=μ となり矛盾するから, μκ < μμ* である.故に仮定26より κ < μ* である.
(27 ⇒ 7)命題10の3より κ**=(κ+κ*)* だから仮定27により κ*=κ+κ* となる.
(28 ⇒ 6) (κ2)*=κ*≦κ+κ*≦κ2+κ* だから,仮定28により κ*=κ+κ* または κ+κ*=κ2+κ* である.もし κ*=κ+κ* ならば κ≦κ* だから命題4により κ2=κ である.
そこで κ+κ*=κ2+κ* とすると κ≦κ2≦κ+κ* となる.よって再び仮定28により κ=κ2 または κ2=κ+κ* である. κ2=κ+κ* と仮定すると κ*≦κ2 だから命題8より κ*≦κ となり矛盾する.故に κ=κ2 である.
(29 ⇒ 30)明らか.
(30 ⇒ 3) κ* はアレフだから, κ* < κ** より κ < κ* である.
(31 ⇒ 32)明らか.
(32 ⇒ 7) κ* < κ+κ* と仮定する.命題10の3より κ**=(κ+κ*)* だから,仮定32より κ** < (κ+κ*)*=κ** となり矛盾する.従って κ*=κ+κ* である.
(33 ⇒ 3) κ**≦κ*+κ と仮定する. κ** はアレフだから命題4より (κ**)2=κ** となる.故に (κ**)2≦κ*+κ だから命題6より「 κ**≦κ* または κ**≦κ 」となり矛盾する.従って κ**![]() κ*+κ であるから,仮定33より κ*=κ*+κ となる.従って κ≦κ* である.
κ*+κ であるから,仮定33より κ*=κ*+κ となる.従って κ≦κ* である.
(34 ⇒ 35)明らか
(35 ⇒ 3) κ+κ*≦κ+κ* だから仮定35より「 κ+κ*≦κ または κ+κ*≦κ* 」となる. κ+κ*≦κ と仮定すると κ*≦κ となり矛盾するから κ+κ*≦κ* ,従って κ≦κ* である.
(36 ⇒ 37)明らか
(37 ⇒ 3) κ・κ*≦κκ* だから仮定35より「 κ・κ*≦κ または κ・κ*≦κ* 」となる. κ・κ*≦κ と仮定すると κ*≦κ となり矛盾するから κ・κ*≦κ* ,従って κ≦κ* である.
※条件6「 κ2=κ 」は選択公理と同値であるが, 2・κ=κ は選択公理と同値ではない.
※条件12「 κ2 =λ2 ならば κ=λ 」は選択公理と同値であるが,「 2・κ=2・λ ならば κ=λ 」は ZF で成り立つ.
※条件19「 κ < λ ならばある μ が存在して λ=κ・μ 」は選択公理と同値であるが,「 κ < λ ならばある μ が存在して λ=κ+μ 」は ZF で成り立つ.(命題1)
定理12
選択公理
⇔ 無限濃度 κ, λ に対して以下が成り立つ.
「κ≦λ < 2κ かつある μ が存在して κ=μ2」ならばある ν が存在して λ=ν2.
証明 ( ⇒ )明らか.
( ⇐ )定理11の条件2を示す. κ を無限濃度として λ:=κ![]() 0 とおく. λ2=κ2・
0 とおく. λ2=κ2・![]() 0=κ
0=κ![]() 0=λ である.命題10の1より λ*≦22λ2=22λ となるから 2λ≦2λ+λ*≦2λ+22λ=22λ である.
0=λ である.命題10の1より λ*≦22λ2=22λ となるから 2λ≦2λ+λ*≦2λ+22λ=22λ である.
もし 2λ+λ*=22λ であれば, ![]() 0≦λ≦2λ だから命題3より λ*=22λ となり κ≦λ≦22λ=λ* である.
0≦λ≦2λ だから命題3より λ*=22λ となり κ≦λ≦22λ=λ* である.
そこで 2λ+λ* < 22λ とする.このとき 2λ≦2λ+λ* < 22λ かつ 2λ=(2λ)2 だから,仮定によりある ν が存在して 2λ+λ*=ν2 と書ける.故に命題7により ν≦λ* または ν≦2λ である.もし ν≦λ* であれば
κ≦λ≦2λ≦2λ+λ*=ν2≦(λ*)2=λ*
である.
そこで ν≦2λ とする.このとき λ≦λ+λ*≦2λ+λ*=ν2≦(2λ)2=2λ である.
もし λ+λ*=2λ (=(2λ)2) ならば命題7により 2λ≦λ または 2λ≦λ* だから κ≦λ≦2λ≦λ* となる.
そこで λ+λ* < 2λ とする.このとき λ≦λ+λ* < 2λ かつ λ=λ2 だから仮定によりある μ が存在して λ+λ*=μ2 と書ける.故に命題7により μ≦λ または μ≦λ* である. μ≦λ と仮定すると λ*≦λ+λ*=μ2≦λ2=λ となり矛盾する.故に μ≦λ* であり κ≦λ+λ*=μ2≦λ* となる.
定理13
選択公理
⇔ 無限濃度 κ, λ に対して「 κ≦λ < 2κ ならばある μ が存在して λ=κ・μ 」.
証明 ( ⇒ )明らか.
( ⇐ )定理11の条件2を示す.前定理の証明と同様である. κ を無限濃度として λ:=κ![]() 0 とおく. 2λ≦2λ+λ*≦22λ である.
0 とおく. 2λ≦2λ+λ*≦22λ である.
もし 2λ+λ*=22λ であれば κ≦λ≦22λ=λ* であるから, 2λ+λ* < 22λ とする.このとき 2λ≦2λ+λ* < 22λ だから,仮定によりある μ が存在して 2λ+λ*=λ・μ と書ける.故に命題7により λ≦λ* または μ≦2λ である.もし λ≦λ* であれば κ≦λ≦λ* となる.
そこで μ≦2λ とする.このとき λ≦λ+λ*≦2λ+λ*=λ・μ≦(2λ)2=2λ である.
もし λ+λ*=2λ ならば κ≦λ≦2λ≦λ* であるから, λ+λ* < 2λ とする.このとき λ≦λ+λ* < 2λ だから仮定によりある ν が存在して λ+λ*=λ・ν と書ける.故に命題7により ν≦λ または λ≦λ* である. ν≦λ と仮定すると λ*≦λ+λ*=λ・ν≦λ2=λ となり矛盾する.故に λ≦λ* であり κ≦λ≦λ* となる.
定理14 選択公理 ⇔ 無限集合 X に対し |X|=|Pfin(X)| .
証明 ( ⇒ )命題9より明らか.
( ⇐ )定理11の条件6を示す. X を集合とするとき X×X = { <a, b> | a, b∈X } で, <a, b> = { {a}, {a, b} } が順序対の定義だったから X×X⊂Pfin(Pfin(X)) .故に
|X|≦|X×X|≦|Pfin(Pfin(X))|=|Pfin(X)|=|X|.
定義 κ を濃度とする. κ=|X| となる X を取り e(κ):=|Pfin(X)| と定める.
命題18
κ, λ を無限濃度, ![]() をアレフとする.
をアレフとする.
- e(
 )=
)= .
. - e(κ+λ)=e(κ)・e(λ) .
- κ・
 0=κ ならば e(κ・
0=κ ならば e(κ・ )=e(κ)・e(
)=e(κ)・e( ) .
) .
証明 (1)命題9より明らか.
(2) 互いに素な無限集合 X, Y に対して f: Pfin(X)×Pfin(Y)→Pfin(X∪Y) を f(A, B):=A∪B と定めれば f は全単射である.
(3)2より e(κ・![]() )=e(κ+
)=e(κ+![]() ) を示せばよい.命題2より κ+
) を示せばよい.命題2より κ+![]() ≦κ・
≦κ・![]() だから e(κ+
だから e(κ+![]() )≦e(κ・
)≦e(κ・![]() ) である.
) である.
逆を示す.今仮定より κ・![]() 0=κ だから e(κ・
0=κ だから e(κ・![]() )≦e(κ・
)≦e(κ・![]() 0+
0+![]() ) を示せばよい. κ=|X|,
) を示せばよい. κ=|X|, ![]() =|W|, (N×X)∩W= ∅ として f: Pfin(X×W)→Pfin((N×X)∪W) を以下のように定める. A∈Pfin(X×W) とする. w∈W に対して Aw:= { x∈X|(x, w)∈A } と置けば,ある w1, …, wn∈W が一意に存在して
=|W|, (N×X)∩W= ∅ として f: Pfin(X×W)→Pfin((N×X)∪W) を以下のように定める. A∈Pfin(X×W) とする. w∈W に対して Aw:= { x∈X|(x, w)∈A } と置けば,ある w1, …, wn∈W が一意に存在して
A=∪i=1n(Awi× { wi } ), w1 < w2 < … < wn
と書ける.このとき f(A):= { w1, …, wn } ∪∪i=1n( { i } ×Awi) と定める.この f は単射である.よって e(κ・![]() )≦e(κ・
)≦e(κ・![]() 0+
0+![]() ) である.
) である.
定理19
κ, λ は無限濃度, ![]() はアレフを表すとする.次の命題は( ZF 上)同値.
はアレフを表すとする.次の命題は( ZF 上)同値.
- 選択公理
- e(κ)=κ .
- e(κ+λ)=e(κ)+e(λ) .
- e(κ+
 )=e(κ)+e(
)=e(κ)+e( ) .
) . - e(κ)=e(λ), κ≦λ⇒κ=λ .
- e(κ+λ)=e(κ) または e(κ+λ)=e(λ) .
- e(κ+e(κ)*)=e(κ)* .
証明 1 ⇔ 2は定理14である.
(1 ⇒ その他)1 ⇔ 2により明らか.
(3 ⇒ 4)明らか.
(4 ⇒ 1)定理11の2を示す. e(κ)* はアレフだから仮定4により e(κ+e(κ)*)=e(κ)+e(e(κ)*)=e(κ)+e(κ)* となる.一方命題18により e(κ+e(κ)*)=e(κ)・e(e(κ)*)=e(κ)・e(κ)* となる.従って e(κ)・e(κ)*≦e(κ)+e(κ)* だから命題6より e(κ)*≦e(κ) または e(κ)≦e(κ)* となる.故にHartogs numberの性質より e(κ)≦e(κ)* となり κ≦e(κ)≦e(κ)* が分かる.
(5 ⇒ 1)定理11の2を示す. λ:=κ・![]() 0 とおく.命題18を使って e(λ+λ*)=e(λ)・e(λ*)=e(λ・λ*) が分かる.命題2より λ+λ*≦λ・λ* だから仮定5より λ+λ*=λ・λ* となる.従って命題6とHartogs numberの性質から κ≦λ≦λ* となる.
0 とおく.命題18を使って e(λ+λ*)=e(λ)・e(λ*)=e(λ・λ*) が分かる.命題2より λ+λ*≦λ・λ* だから仮定5より λ+λ*=λ・λ* となる.従って命題6とHartogs numberの性質から κ≦λ≦λ* となる.
(6 ⇒ 7)明らか.
(7 ⇒ 1)定理11の2を示す. κ≦κ+e(κ)*≦e(κ+e(κ)*)=e(κ)* .
定理
選択公理
⇔ X を集合,{ Xi }i=0∞ を集合族として |X| < |∪i=0∞Xi| を満たすとする.このときある n∈N が存在して |X|≦|∪i=0nXi| .
証明
( ⇒ )任意の n∈N に対して |X|![]() |∪i=0nXi| と仮定する.選択公理により濃度は比較可能であるから |∪i=0nXi| < |X| となる.よって |Xi|≦|X| であり |∪i=0∞Xi|≦
|∪i=0nXi| と仮定する.選択公理により濃度は比較可能であるから |∪i=0nXi| < |X| となる.よって |Xi|≦|X| であり |∪i=0∞Xi|≦![]() 0・|X|=|X| となって矛盾する.
0・|X|=|X| となって矛盾する.
( ⇐ )整列可能定理を示す.その為 X を任意の集合とする. Y0:=X, Yi+1:=P(Yi), Y:=∪i=0∞Γ(Yi) と定める. Y は整列可能である.各 i∈N について標準的な単射 Γ(Yi)→P(P(P(Yi)))=Yi+3 が構成できるから |Y|≦|∪i=0∞( { i } ×Yi)| である.
|Y| < |∪i=0∞( { i } ×Yi)| と仮定する.ある n∈N が存在して |Y|≦|∪i=0n( { i } ×Yi)| となる.よってある Zi⊂Yi が存在して |Y|=|∪i=0n( { i } ×Zi)| とできる. Y が整列可能だから Zi も整列可能であり |Y|=|∪i=0n( { i } ×Zi)|=∪i=0n|Zi|=max0≦i≦n|Zi| となる. |Zj|=max0≦i≦n|Zi| となる j を取れば |Γ(Yj)|≦|Y|=|Zj|≦|Yj| となり矛盾する.
故に |Y|=|∪i=0∞( { i } ×Yi)|≧|Y0|=|X| となり, X は整列可能である.
定理 次の命題は( ZF 上)同値.
- 選択公理
- 任意の集合 X に対してある集合 Y が存在して Y = { x⊂Y | |X|
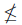 |x| } .
|x| } . - 任意の集合 X に対してある集合 Y が存在して |Y| = |{ x⊂Y | |X|
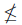 |x| }| .
|x| }| .
証明 (1 ⇒ 2) X を任意の集合とする. α := Γ(Γ(P(X))) とおき, β < α に対して
f(β) := { x⊂∪γ<βf(γ) | |x| < |X| }
と定め, Y := ∪β<αf(β) とする.この Y が Y = { x⊂Y | |X|![]() |x| } を満たす.
|x| } を満たす.
(⊂) x∈Y とする. Y の定義よりある β < α が存在して x∈f(β) となる.故に x⊂Y かつ |x| < |X| ,即ち |X|![]() |x| である.従って x∈{ x⊂Y | |X|
|x| である.従って x∈{ x⊂Y | |X|![]() |x| } .
|x| } .
(⊃) x⊂Y かつ |X|![]() |x| とする.選択公理により,濃度が比較可能だから |x|≦|X| である. a∈x に対して Ba := { β < α | a∈f(β) } , γa := minBa と定め, R := { γa | a∈x }とする. R は順序数の集合だから |R|≦|x| となる.故に |R| < 2|R|≦2|x|≦2|X| である. R は順序数の集合だから整列可能であり,よって Γ の性質から |R| < |α| が分かる. θ:=supR と置く.明らかに |θ|≦|∪β∈R( { β } ×β)| である. β∈R とすれば β < α だったから |β| < |α| である. δ:=Γ(P(X)) とすれば α=Γ(δ) だから |β|≦|δ| となる. β∈R に対して Aβ:= { f: β→δ|f は単射 } ≠ ∅ と定める.選択公理により (fβ)∈Πβ∈RAβ が取れる.これにより |∪β∈R( { β } ×β)|≦|∪β∈R({β}×δ)| である.よって
|x| とする.選択公理により,濃度が比較可能だから |x|≦|X| である. a∈x に対して Ba := { β < α | a∈f(β) } , γa := minBa と定め, R := { γa | a∈x }とする. R は順序数の集合だから |R|≦|x| となる.故に |R| < 2|R|≦2|x|≦2|X| である. R は順序数の集合だから整列可能であり,よって Γ の性質から |R| < |α| が分かる. θ:=supR と置く.明らかに |θ|≦|∪β∈R( { β } ×β)| である. β∈R とすれば β < α だったから |β| < |α| である. δ:=Γ(P(X)) とすれば α=Γ(δ) だから |β|≦|δ| となる. β∈R に対して Aβ:= { f: β→δ|f は単射 } ≠ ∅ と定める.選択公理により (fβ)∈Πβ∈RAβ が取れる.これにより |∪β∈R( { β } ×β)|≦|∪β∈R({β}×δ)| である.よって
|θ|≦|∪β∈R({β}×β)|≦|∪β∈R({β}×δ)|≦|R×δ|=|δ|
となり |θ| < |α| が成り立つ.
a∈x とするとある β∈R が存在して a∈f(β) である.よって x⊂∪β < θ+1f(β) となる. |θ| < |α| だから θ+1 < α である.よって, |x| < |X| だったから, x∈f(θ+1)⊂Y が分かった.
(2 ⇒ 3)明らか.
(3 ⇒ 1)整列可能定理を示す. X を任意の集合とする.仮定3よりある Y が存在して |Y| = |{ A⊂Y | |X|![]() |A| }| となる. S:= { A⊂Y | |X|
|A| }| となる. S:= { A⊂Y | |X|![]() |A| } と置き単射 f: S→Y と ∞ ∉ Y を取る.順序数 α に対して
|A| } と置き単射 f: S→Y と ∞ ∉ Y を取る.順序数 α に対して
g(α) := f(g''α) (g''α∈Sのとき)
g(α) := ∞ (そうでないとき).
と定める. g(α)≠∞, g(β)≠∞ で g(α)≠g(β) ならば α≠β である.故に順序数 γ で g(γ)=∞ なるものが存在する.そのような γ のうち最小の γ を取っておけば W := g''γ⊂Y で, W = g''γ ∉ S である.よって |X|≦|W| となり, W は整列可能だから X も整列可能となる.
参考文献
- Horst Herrlich, Axiom of Choice,Springer, 2006
- H. Rubin and J. Rubin, Equivalents of the axiom of choice, North Holland, 1963.
コメント
コメントはまだありません。