定理1 選択公理
⇔を位相空間の族とし，集合族{A_λ}_λ∈Λは任意のλ∈ΛについてA_λ⊂ X_λを満たすとする．このとき

cl(Π_λ∈ΛA_λ)⊃Π_λ∈Λcl(A_λ)

左辺の cl はでの閉包，右辺の cl は各X_λでの閉包である．
また，逆向きの包含関係 cl(Π_λ∈ΛA_λ)⊂Π_λ∈Λcl(A_λ) は(選択公理によらず)常に成り立つ．

証明 (⇒) x=(x_λ)∈Π_λ∈Λcl(A_λ)を取る． λ∈Λに対してx_λ∈cl(A_λ)だから， x_λの任意の開近傍U⊂ X_λに対しU∩ A_λ≠∅となる． xの任意の開近傍U⊂を取る． 族{U_λ}_λ∈Λが，各U_λはX_λの開集合で Π_λ∈ΛU_λ⊂ Uとなるように取れる． このとき各λ∈ΛについてU_λ∩ A_λ≠∅． 故に選択公理によりΠ_λ∈Λ(U_λ∩ A_λ)≠∅となる． 従ってU∩ A=Π_λ∈Λ(U_λ∩ A_λ)≠∅である． よってx∈cl(Π_λ∈ΛA_λ)．

(←) {A_λ}_λ∈Λを空でない集合の族とする．￢∞∈∪_λ∈ΛA_λとなる∞を一つ用意し，X_λ := A_λ∪{∞}と置く．X_λに密着位相を入れる．明らかに≠∅．このとき

cl(Π_λ∈ΛA_λ)⊃Π_λ∈Λcl(A_λ)=≠∅.

(Π X_λの中で考えて) cl(∅)=∅だから，Π_λ∈ΛA_λ≠∅でなければならない．

定理2 以下の命題は(ZF上)同値．

1. 選択公理
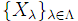2. を位相空間の族とし， {A_λ}_λ∈Λは任意のλ∈Λについて ∅≠ A_λ⊂ X_λを満たすとする．このとき

   Π_λ∈ΛA_λ⊂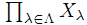が閉集合 ⇒ 任意のλ∈Λ に対しA_λ⊂ X_λが閉集合

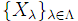3. を位相空間の族とし， {A_λ}_λ∈Λは任意のλ∈Λについて ∅≠ A_λ⊂ X_λを満たすとする．このとき

   Π_λ∈ΛA_λ⊂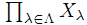が閉集合 ⇒ あるλ∈Λ に対しA_λ⊂ X_λが閉集合

証明 (1⇒2) 定理1によりΠ_λ∈ΛA_λ =cl(Π_λ∈ΛA_λ)=Π_λ∈Λcl(A_λ) である．よって選択公理によりA_λ = cl(A_λ) である(集合に関する命題の定理7を参照)．即ちA_λ⊂ X_λは閉集合である．

(2⇒3) 明らか．

(3⇒1) 選択公理が成り立たないと仮定する．すると非空集合の族{A_λ}_λ∈ΛでΠ_λ∈ΛA_λ=∅となるものが存在する．￢∞∈∪_λ∈ΛA_λなる∞を一つ用意し，X_λ := A_λ∪{∞}と定める．各X_λには密着位相を入れる．∅=Π_λ∈ΛA_λはの閉集合だから， 仮定3より，あるλ∈Λが存在してA_λ⊊ X_λが閉集合となる． X_λには密着位相が入っていたから，A_λ=∅でなければならず，矛盾する．

次の命題はZFで証明できる．

命題 を位相空間の族とし， 族{A_λ}_λ∈Λは任意のλ∈Λについて ∅≠ A_λ⊂ X_λを満たすとする． またΠ_λ∈ΛA_λ≠∅であるとする． このとき

Π_λ∈ΛA_λ⊂が閉集合 ⇒ 任意のλ∈Λ に対しA_λ⊂ X_λが閉集合

証明 命題の仮定を満たすと{A_λ}_λ∈Λを取る． Π_λ∈ΛA_λ≠∅だから，(a_λ)∈Π_λ∈ΛA_λが取れる．

あるμ∈Λが存在してA_μ⊂ X_μが閉集合でないと仮定する． p∈cl(A_μ)＼ A_μが取れる． 写像f: Λ→を

f(μ) := p
λ≠μに対し f(λ) := a_λ

と定める．明らかにf∈かつf∉Π_λ∈ΛA_λである．Π_λ∈ΛA_λ⊂は閉集合だから，fの開近傍U⊂でU∩Π_λ∈ΛA_λ=∅となるものが存在する．族{U_λ}_λ∈Λを，各U_λはX_λの開集合で，Π_λ∈ΛU_λ⊂ Uとなるように取る．このとき

∅=U∩Π_λ∈ΛA_λ ⊃Π_λ∈ΛU_λ∩Π_λ∈ΛA_λ ⊃Π_λ∈Λ(U_λ∩ A_λ)

である．p∈U_μかつp∈ cl(A_μ)だから， U_μ∩A_μ≠∅である．そこでq∈ U_μ∩ A_μを一つ取り，写像g: Λ→を

g(μ) := q
λ≠μに対し g(λ) := a_λ

で定めれば，g∈Π_λ∈Λ(U_λ∩ A_λ)=∅となり矛盾する．