整列可能定理について

PDF版

定理1 次の命題は同値

任意の集合は整列可能．
任意の全順序集合は整列可能．
集合 X が整列可能ならば冪集合 P(X) も整列可能．

証明 (1⇒2) 自明

(2⇒3) 「任意の順序数αに対して P(α) は整列可能」を示せばよい． P(α)に順序 < を

A<B ⇔ ∃a∈A＼B(∀b∈B＼A (a<b) )

で定める(ただし，a<bは順序数αの順序)．この順序によってP(α)が全順序集合になることを確かめる．

(i) ￢A<A について．
A＼A= ∅ なので明らか

(ii) A<B ⇒ ￢B<A について．
A<Bとすると < の定義より，あるa₀∈A＼Bが有って∀b∈B＼A(a₀<b)となる．よって明らかに￢∃b∈B＼A(∀a∈A＼B (b<a) )，即ち￢B<Aである．

(iii) A<B または A=B または B<A について．
(￢A<Bかつ￢B<A) ⇒ A=B を示す．A≠Bと仮定する．A＼B≠∅としても一般性を失わない．<の定義より

(1)　∀a∈A＼B(∃b∈B＼A (b≦a) )
(2)　∀b∈B＼A(∃a∈A＼B (a≦b) )

である．αは整列順序集合なので a₀ := min(A＼B) が存在する．このa₀に対し(1)から∃b₀∈B＼A(b₀≦a₀)である．このb₀に対し(2)から∃a₁∈A＼B(a₁≦ b₀)．a₀の最小性よりa₀≦a₁，従ってa₀≦a₁≦b₀≦a₀となる．故にa₀ = b₀∈(A＼B)∩(B＼A) = ∅ となり矛盾．

(iv)(A<B かつ B<C) ⇒ A<C について．
￢A<Cと仮定する．A=CだとするとA<B∧B<Aとなり(ii)に反するのてA≠Bである．故に(iii)からC<Aである．A<B, B<C, C<Aより

(3)　∃a∈A＼B(∀b∈B＼A (a<b) )
(4)　∃b∈B＼C(∀c∈C＼B (b<c) )
(5)　∃c∈C＼A(∀a∈A＼C (c<a) )

これらを満たすa₀∈A＼B, b₀∈B＼C, c₀∈C＼Aを取る．a₀∈A＼Cである．

a₀∉A＼Cと仮定する．即ちa₀∈A^c∪C．a₀∈A＼Bだったからa₀∈(A^c∪C)∪(A＼B)=A∪C＼B⊂C＼Bである．よって(4)により b₀ < a₀．従って(3)から b₀ ∉ B＼A でなければならない．すると同様の議論を繰り返して a₀ < c₀ < b₀ < a₀ が導かれ，矛盾．

同様にしてb₀∈B＼A, c₀∈C＼Bである．従って(3)(4)(5)から a₀<b₀<c₀<a₀ となり，矛盾する．

以上より(P(α), <)は全順序集合である．よって，仮定より整列可能である．

(3⇒1) Xを任意の集合とすると基礎の公理により順序数αが存在してX⊂R(α)となる．

基礎の公理とはZFに含まれる公理の1つで x≠∅ ⇒ ∃y∈x( x∩y = ∅ ) を表す．また，順序数αに対しR(α)は
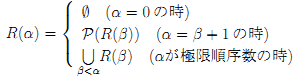
R(α)の定義
と定義される．このとき「ZFから基礎の公理を除いた公理系」の元で基礎の公理と∀x∃α：順序数(x∈R(α))は同値になる．

故にR(α)が整列可能であることを示せば十分である．

α= 0 の時．R(0)=∅は明らかに整列可能である．

α=β+1 の時．R(α) = P(R(β)) で，帰納法の仮定からR(β)は整列可能，よって仮定よりR(α)も整列可能である．

αが極限順序数の時．R(α)=∪_{β<α}R(β) で，帰納法の仮定から各R(β)は整列可能である．もしα上の関数Sで
任意のβ<αに対しS(β)はR(β)の整列順序
となるようなものがあれば，R(α)は整列可能である．

R(α)上の二項関係
≦ := { <u, v>∈R(α)^2 | ρ(u)<ρ(v)∨(ρ(u)=ρ(v)∧uS(ρ(u)+1)v) } を考える．これがR(α)の整列順序関係になる事を示す．

ここでρ(u)とはu∈R(β+1)となるような最小の順序数βの事．

(i) u≦u について．
uS(ρ(u)+1)uから明らか．

(ii)(u≦v∧v≦u)⇒u=v について．
u≦v∧v≦uとするとρ(u)=ρ(v)である．即ちuS(ρ(u)+1)vかつvS(ρ(u)+1)u．S(ρ(u)+1)が反対称律を満たすのでu=vである．

(iii)(u≦v∧v≦w)⇒u≦w について．
ρ(u)<ρ(v)またはρ(v)<ρ(w)の時は明らかなのでρ(u)=ρ(v)=ρ(w)とする．この時uS(ρ(u)+1)vかつvS(ρ(u)+1)wであり，S(ρ(u)+1)の推移律よりuS(ρ(u)+1)wである．

以上より(R(α), ≦)は順序集合である．次に任意の部分集合A⊂R(α)をとる．ρ(u) (u∈ A)と表されるような最小の順序数をξとする．次にB:={u∈ A|ρ(u)=ξ}を考える．B⊂R(ξ+1)であり，S(ξ+1)はR(ξ+1)を整列するからBは最小元u₀を持つ．u₀の選び方から，これはAの最小元である．即ち(R(α), ≦)は整列順序集合である．

そのようなSを定義するため，まず十分大きい順序数δを取っておく．仮定によりP(δ)は整列可能なので，その整列順序rを1つとる．s(β) (β<α)を帰納法により定義する．

β= 0 の時．S(0):=∅．これは明らかにR(0)を整列する．

β=γ+1 の時．整列集合(R(γ), S(γ))と順序同型な順序数ξをとり，f: R(γ)⇒ξを順序同型写像とする．δが十分大きければξ≦δなので，fはR(γ)からδの中への順序同型とみなせる．そこでS(β)をfと(P(δ), r)から自然に導かれるR(β)の整列順序とする．

βが極限順序数の時．

S(β) := { <u, v>∈ R(β)^2 | ρ(u)<ρ(v)∨(ρ(u)=ρ(v)∧uS(ρ(u)+1)v) }

とすれば，これは整列順序になる．

この定義が上手くいくためには全てのβ<αについてOrd(R(β), S(β))<δでなければならない．その為にはδ= $(sup_{β<α}|R(β)|)^+$ とすれば良い．

定理2 整列可能定理⇔選択関数を持つ集合は整列可能

証明 ⇒は明らか． ←を示す．任意の集合Xに対し Y := { {x} | x∈X } と置けば，Yは明らかに選択関数を持つ．故にYは整列可能．よって明らかにXも整列可能．

定理3 λは基数を表すとし，WO(X, m)で命題

ある順序数αとα上の関数fが存在して∀β<α( |f(β)| <λ ) かつ X=∪_β<α f(β)

を表すことにする．mは2以上の整数を表すとするとき，次の命題は(ZF上)同値．

1. 整列可能定理
2(m). 任意の集合 X に対し WO(X, m)
3. ある m≧2 が存在して任意の集合 X に対し WO(X, m)
4. 任意の集合 X に対しある m≧2 が存在して WO(X, m)
5. 任意の集合 X に対し WO(X, )

証明 1⇔2(2) と 2(m)⇒3 と 3⇒4 と 4⇒5 は明らか．m≦n に対し 2(m)⇒2(n) も明らか．なので 5⇒1 を示せばよい．その為には選択公理と同値なAMCを示せばよい．

AMC(=the Axiom of Multiple Choice)とは次の命題のこと．

集合Xが￢ ∅ ∈X を満たす時， X上の写像fが存在して，任意のx∈Xに対し f(x)⊂x, 0 < |f(x)| <∞ を満たす

同値性の証明はthe Axiom of Multiple Choiceを参照．

Xを集合とし，￢ ∅ ∈X とする．仮定5により WO(∪X, ) の条件を満たす順序数αと写像 g が存在する．x∈X に対し β(x) := min{ γ< α | x∩g(γ) ≠ ∅ } と定めて f(x) := x∩g(β(x)) と置けば，この f がAMCを満たす．

基礎の公理を仮定しないと AMC⇒選択公理は証明できない．つまりこの 5⇒1 の証明は基礎の公理を使っていることになる．実は 5⇒1 は基礎の公理を仮定しないと証明できないことが知られている．( 5⇔AMC は基礎の公理を使わずに証明できる．)一方，4⇒1 は基礎の公理を使わなくても証明できるので，その証明を書いておく．

証明まず Y×Y⊂Y を満たす集合 Y が整列可能であることを示す．m>1 で WO(Y, m) が成立しているとする． (この時 WO(Y, m-1) であることをこれから示す．) WO(Y, m) の条件を満たす順序数αと関数 f を取り

u(β, γ, δ) := (f(β)×f(γ))∩f(δ)　(β, γ, δ<α)

を考える．定義より u(β, γ, δ) は二項関係とみなせる． (即ち定義域 dom，値域 ran を考えることができる．) fの性質から

| dom(u(β, γ, δ)) |≦| f(β) |≦m
| ran(u(β, γ, δ)) |≦| f(γ) |≦m
| u(β, γ, δ) |≦| f(δ) |≦m

である．

(i)全てのβ<αに対し「f(β)≠∅⇒∃γ, δ<α(0< |dom(u(β, γ, δ))| <m)」の時．
f(β)≠ ∅ なるβ<αに対し，0<| dom(u(β, γ, δ)) |<mとなる組<γ, δ>のうち辞書式順序で最小のものを<λ_β, μ_β>で表す．

f(β)≠ ∅ の時　v_β := dom(u(β, λ_β, μ_β))
f(β)= ∅ の時　v_β := ∅
w_β := f(β)＼v_β

と置き，α+α上の関数gを

β<αの時　g(β) := v_β
α≦β, β＼α≅γ<αの時　g(β) := w_γ

で定義する．すると∪_β<α+α g(β) = y である．次に，定義から明らかに | v_β|<m, | w_β|<m だから | g(β) |≦m-1　(β<α+α)である．即ち，α+αとgが WO(Y, m-1) の条件を満たす．

f(γ)≠ ∅ の時　v_γ := { u(β, γ, δ_γ)(s) }
f(γ)= ∅ の時　v_γ:= ∅
w_γ := f(γ)＼v_γ

と置き，α+α上の関数gを

γ<αの時　g(γ) := v_γ
α≦γ, γ＼α≅λ<αの時　g(γ) := w_λ

で定義する．すると(i)の場合と同様，α+αとgが WO(Y, m-1) の条件を満たす．

(i)(ii)より WO(Y, m-1) が成立する．仮定4. より WO(Y, m) が成立するmは存在するから，WO(Y, 1)が成立することが分かる．即ち，Y は整列可能である．

さて，X を任意の集合とする．この時

Z₀ := X, Z_n+1 := Z_n ∪(Z_n×Z_n), Y := ∪_n=0∞ Z_n

と置く．すると m<n の時 Z_m ⊂ Z_n, Z_m×Z_m ⊂ Z_n だから

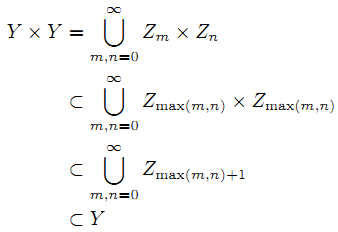
$Y×Y=∪_{m, n=0}^{∞}Z_m×Z_n⊂∪_{m, n=0}^{∞}Z_{max(m, n)}×Z_{max(m, n)}⊂∪_{m, n=0}^{∞}Z_{max(m, n)+1}⊂Y$

よって先に述べた通り Y は整列可能であり，明らかに X⊂Y だから X も整列可能である．

参考文献

Horst Herrlich『Axiom of Choice』
Azriel Levy『Basic set theory』pp164-165
H. Rubin and J. Rubin『Equivalents of the axiom of choice, II』

コメントはまだありません。

整列可能定理について

参考文献

コメント

コメントする