位相空間の直積・直和

定理1 選択公理
⇔ { X_λ }_λ∈Λ と { Y_λ }_λ∈Λ は位相空間の族で，各 λ∈Λ について X_λ ≅ Y_λ (同相)とする．このとき Π_λ∈ΛX_λ ≅ Π_λ∈ΛY_λ である．

証明 ( ⇒ ) H_λ := { f: X_λ→Y_λ | f は同相写像 } と置けば仮定により H_λ≠ ∅である．選択公理によって (f_λ)_λ∈Λ∈Π_λ∈ΛH_λ を取る． f: Π_λ∈ΛX_λ→Π_λ∈ΛY_λ を f((x_λ)_λ∈Λ) := (f_λ(x_λ))_λ∈Λ で定めれば f は同相写像である．

( ⇐ ) { X_λ }_λ∈Λ を非空集合の族とする．まず，各 X_λ がDedekind無限であるとする．

「集合 X がDedekind無限 ⇔ X に含まれない元 ∞ に対して |X|=|X∪{∞}| 」が成り立つ．定義などは有限集合・無限集合の定義を参照．

どの X_λ にも含まれない元 ∞ を一つ取り， Y_λ := X_λ∪{∞} とする． X_λ, Y_λ に離散位相を入れると， |X_λ| = |Y_λ| だから X_λ ≅ Y_λ である．故に仮定から Π_λ∈ΛX_λ ≅ Π_λ∈ΛY_λ≠ ∅ が分かる．

X_λ がDedekind無限とは限らないときは Z_λ := X_λ×N と置く． Z_λ はDedekind無限だから，既に示したように Π_λ∈ΛZ_λ≠ ∅ である．よって元 (<x_λ, n_λ>)_λ∈Λ∈Π_λ∈ΛZ_λ が取れるが，このとき (x_λ)_λ∈Λ∈Π_λ∈ΛX_λ である．

この定理の ⇐ の証明では X_λ や Y_λ が離散位相である場合しか使っていない．故に次の系が分かる．

系2 次の命題は( ZF 上)同値．

選択公理
{ X_λ }_λ∈Λ と { Y_λ }_λ∈Λ は集合族で，各 λ∈Λ について |X_λ| = |Y_λ| とする．このとき |Π_λ∈ΛX_λ| = |Π_λ∈ΛY_λ| である．
{ X_λ }_λ∈Λ と { Y_λ }_λ∈Λ は離散位相空間の族で，各 λ∈Λ について X_λ ≅ Y_λ とする．このとき Π_λ∈ΛX_λ ≅ Π_λ∈ΛY_λである．
{ X_λ }_λ∈Λ と { Y_λ }_λ∈Λ は距離空間の族で，各 λ∈Λ について X_λ ≅ Y_λ とする．このとき Π_λ∈ΛX_λ ≅ Π_λ∈ΛY_λである．
{ X_λ }_λ∈Λ と { Y_λ }_λ∈Λ は一様空間の族で，各 λ∈Λ について X_λ ≅ Y_λ とする．このとき Π_λ∈ΛX_λ ≅ Π_λ∈ΛY_λである．

定理3 選択公理
⇔ { X_λ }_λ∈Λ と { Y_λ }_λ∈Λ はコンパクトHausdorff空間の族で，各 λ∈Λ について X_λ ≅ Y_λ とする．このとき Π_λ∈ΛX_λ ≅ Π_λ∈ΛY_λである．

証明 ( ⇒ )明らか．

( ⇐ ) { X_λ }_λ∈Λ を非空集合の族とする．次の性質を満たすようなDedekind無限集合 K を取ることができる: { F_λ }_λ∈Λが有限集合の族ならばK ⊄ ∪_λ∈ΛF_λである.

A := { | 全射 Λ×N→ が存在する } として |K| > supA となるような整列順序集合 K を取ればよい．

この K が条件を満たすことを示すため，有限集合の族 { F_λ }_λ∈Λ が K⊂∪_λ∈ΛF_λ を満たすと仮定する． K=∪_λ∈ΛF_λ としてよい．このとき K の整列順序により各 F_λ に順序が入る．これを使って F_λ = { x_λ⁰, …, x_λ^n_λ-1 } と書くことが出来る．元 a∈K を一つ取り，写像 f: Λ×N→K を

f(λ, n) := x_λⁿ　(n < n_λのとき)
f(λ, n) := a　(それ以外).

により定める．この f は明らかに全射である．故に |K|∈A となるが，それは |K| > supA に矛盾する．

前定理のときと同様，必要ならば X_λ×K を考えることにより， |K|≦|X_λ| と仮定しても一般性を失わない．(このとき X_λ はDedekind無限である．)

どの X_λ にも含まれない異なる二つの元 a, b を取る． Y_λ := X_λ∪{ a } を離散位相空間 X_λ の一点コンパクト化， Z_λ := X_λ∪{ a, b } を離散位相空間 X_λ∪{ a } の一点コンパクト化，とする．即ち， Y_λ, Z_λ の位相を

O_{Y_λ} := P(X_λ)∪ { O⊂Y_λ | |Y_λ＼O| < ∞ }
O_{Z_λ} := P(Y_λ)∪ { O⊂Z_λ | |Z_λ＼O| < ∞ }

で定める．これにより Y_λ, Z_λ はコンパクトHausdorff空間で， Y_λ ≅ Z_λ となる．故に仮定から同相写像 f: Π_λ∈ΛY_λ→Π_λ∈ΛZ_λ が存在する． z := (a)_λ∈Λ∈Π_λ∈ΛZ_λ だから f(y)=z となるような y=(y_λ)_λ∈Λ∈Π_λ∈ΛY_λ が存在する． y∈Π_λ∈ΛX_λ であることを示せば証明が終わる．その為に y ∉ Π_λ∈ΛX_λ と仮定すると，ある μ∈Λ が存在して y_μ∈Y_μ＼X_μ= { a } ，即ち y_μ=a である． A := (Π_λ≠μ { y_λ } )×X_μ⊂Π_λ∈ΛY_λ と置く． |A|=|X_μ|≧|K| である． y の開近傍 U⊂Π_λ∈ΛY_λ を任意に取ると O_{Y_λ} の定義から |A＼U| < ∞ である． B := f(A) と置けば f が同相写像だから， |B| = |A|≧K ，かつ z の任意の開近傍 V⊂Π_λ∈ΛZ_λ に対し |B＼V| < ∞ が分かる． { a }⊂Z_λ は開集合だから |B＼π_λ^-1(a)| < ∞ である． y ∉ A だから z=f(y) ∉ B ，故に

B=B＼{ z } =B＼∩_λ∈Λπ_λ^-1(a)=∪_λ∈Λ(B＼π_λ^-1(a)).

これは K の取り方に反する．

同様のことが，直積を直和に変えても成り立つ．

定理4 次の命題は( ZF 上)同値．

選択公理
{ X_λ }_λ∈Λ と { Y_λ }_λ∈Λ は位相空間の族で，各 λ∈Λ について X_λ ≅ Y_λ とする．このとき 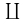$\coprod$ _λ∈ΛX_λ ≅ 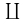$\coprod$ _λ∈ΛY_λである．
{ X_λ }_λ∈Λ と { Y_λ }_λ∈Λ は距離空間の族で，各 λ∈Λ について X_λ ≅ Y_λ とする．このとき 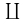$\coprod$ _λ∈ΛX_λ ≅ 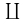$\coprod$ _λ∈ΛY_λである．
{ X_λ }_λ∈Λ と { Y_λ }_λ∈Λ はコンパクトHausdorff空間の族で，各 λ∈Λ について X_λ ≅ Y_λ とする．このとき 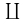$\coprod$ _λ∈ΛX_λ ≅ 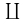$\coprod$ _λ∈ΛY_λである．

証明 1⇒2 と 2⇒3 と 2⇒4 は明らか．

(4 ⇒ 1) { X_λ }_λ∈Λ を互いに素な非空集合の族とする．前定理の証明と同様， X_λ はDedekind無限集合としてよい．どの X_λ にも含まれない元 ∞ を一つ取り Y_λ:=X_λ∪{ ∞ } と置き， X_λ と Y_λ に離散位相を入れる． I := (0, 1]⊂R を半開区間として，直積位相空間 X_λ×I, Y_λ×I を考える．これらは局所コンパクトHausdorff空間である． X_λ^* と Y_λ^* を X_λ×I と Y_λ×I の一点コンパクト化とすると X_λ^* と Y_λ^* は連結なコンパクトHausdorff空間である．

まず X_λ×I の一点コンパクト化 X_λ^* の定義を確認する．( Y_λ×I についても同様．) X_λ×I に含まれない元 a_λ を一つ取り X_λ^* := (X_λ×I)∪{ a_λ } と置く． X_λ^* の位相を

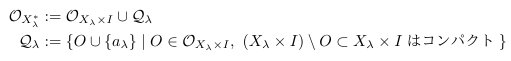
で定める．

まず X_λ^* がコンパクトHausdorff空間であることは簡単に分かる．

次に X_λ^* が連結であることを示す． O₁, O₂⊂X_λ^* を互いに素な開集合で X_λ^*=O₁∪O₂ を満たすとする． a_λ∈O₁ としてよい． O₂≠ ∅ と仮定する．ある x∈X_λ, r∈I が存在して <x, r>∈O₂ である．すると， I は連結だから { x }×I⊂O₂ である． O_{X_λ^*} の定義から (X_λ×I)＼O₁=O₂ は( X_λ×I の)コンパクト閉集合である O₂ がコンパクトだから，その閉部分集合 { x }×I⊂O₂ もコンパクト．しかし，明らかに { x }×I はコンパクトでないから矛盾する．故に O₂= ∅ となり X_λ^* の連結性が分かった．

λ∈Λ とする．このとき X_λ^* ≅ Y_λ^* である．

X_λ がDedekind無限であるから全単射 h_λ: X_λ→Y_λ が存在する．このとき g_λ := h_λ×id_I: X_λ×I→Y_λ×I とすると g_λ は同相写像である． Y_λ^*＼(Y_λ×I)= { b_λ } と書いて， f_λ: X_λ^*→Y_λ^* を

f(y) := g(x)　(x∈X_λ×Iのとき)
f(y) := b_λ　(x=a_λのとき) .

で定めれば f_λ は同相写像である．

よって仮定4から同相写像 f: $\coprod$ _λ∈Λ X_λ^*→ $\coprod$ _λ∈ΛY_λ^* が存在する． X_λ^*, Y_λ^* はそれぞれ $\coprod$ _λ∈Λ X_λ^*, $\coprod$ _λ∈ΛY_λ^* の連結成分である．故にある写像 h: Λ→Λ が存在して，任意の λ∈Λ に対して f(X_λ^*)=Y_h(λ)^* となる． <∞, 1>∈Y_h(λ)×I⊂Y_h(λ)^* だから <x_λ, r_λ> := f^-1(<∞, 1>) と定めると <x_λ, r_λ>∈X_λ×I である．

(3 ⇒ 1) 4⇒1 の証明において X_λ^*, Y_λ^* の位相を次のように変更すればよい． X_λ^* の位相は

a_λの開近傍系を { X_λ×(0, r) | r∈I }
<x, r> の開近傍系を { { x } ×U | r∈U∈O_I }

で定める． Y_λ^* についても同様．

系2の条件2の直和バージョン「 { X_λ }_λ∈Λ と { Y_λ }_λ∈Λ は集合族で，各 λ∈Λ について |X_λ|=|Y_λ| とする．このとき | $\coprod$ _λ∈ΛX_λ|=| $\coprod$ _λ∈ΛY_λ| である」が選択公理と同値かどうかは未解決問題であるが，Partition Principleを導くことは知られている．Partition Principleを参照．

定義 (X, O) を位相空間，U⊂O とする．

V⊂O が U の開細分 ⇔ 任意の V∈V に対してある U∈U が存在して V⊂U となる．
U が局所有限 ⇔ 任意の x∈X に対してある x∈O∈O が存在して | { U∈U | U∩O≠ ∅ } | < ∞ となる．
U が点有限 ⇔ 任意の x∈X に対して | { U∈U | x∈U } | < ∞ となる．
U がshrinkable ⇔ 開被覆 { V_U } _U∈U で，任意の U∈U に対して ∅ ≠cl(V_U)⊂U となるものが存在する．

定義 X を位相空間とする．

X がパラコンパクト ⇔ X の開被覆は局所有限な開細分を持つ．
X がメタコンパクト ⇔ X の開被覆は点有限な開細分を持つ．
X がPFCS ⇔ X の点有限な開被覆はshrinkableである．

定理5 AMC ⇔ パラコンパクト空間の直和はパラコンパクトである．

証明 ( ⇒ ) ${X_λ}_{λ∈Λ}$ をパラコンパクト空間の族として X := $\coprod$ _λ∈ΛX_λ を直和，U を X の開被覆とする．任意の U∈U に対して λ∈Λ が一意に存在して U⊂X_λ となる，としてよい． U_λ := { U∈U | U⊂X_λ }，A_λ := { V | V は U_λ の局所有限な開細分 } と置く． U_λ は X_λ の開被覆で X_λ がパラコンパクトだから， A_λ≠ ∅ である．故に { A_λ }_λ∈Λ にAMCを適用して，有限集合の族 { F_λ }_λ∈Λ を ∅ ≠F_λ⊂A_λ となるように取ることが出来る．このとき V_λ := ∪_{W∈F_λ}W は U_λ の局所有限開細分で， ∪_λ∈ΛV_λ は U の局所有限な開細分である．

( ⇐ ) ${X_λ}_{λ∈Λ}$ を非空集合の族とする．各 X_λ は無限集合としてよい． X_λ に離散位相を入れて X_λ^*=X_λ∪{ ∞_λ } を一点コンパクト化とする． X_λ^* はパラコンパクトだから，仮定により直和 X := $\coprod$ _λ∈ΛX_λ^* もパラコンパクトである．

U := { U⊂X | ある λ∈Λ に対してU⊊X_λ^* かつ U は∞_λ の開近傍 }

は X の開被覆だから，局所有限な開細分 V が存在する．このとき F_λ:=∪_{∞_λ∈U∈V}X_λ＼U は有限集合である．

定理6 AMC ⇔ メタコンパクト空間の直和はメタコンパクトである．

証明定理5と同様．

定理7 AMC ⇔ PFCS空間の直和はPFCSである．

証明 ( ⇒ ) 定理5と同様．

( ⇐ ) ${X_λ}_{λ∈Λ}$ を非空集合の族とする．各 X_λ は無限集合としてよい．定理5の証明と同様の構成をすれば， X_λ^* はPFCSだから仮定より X もPFCSである． U := { X_λ | λ∈Λ }∪{ X_λ^* | λ∈Λ } は X の開被覆だから，開被覆 { V_U }_U∈U で，任意の U∈U に対して ∅ ≠ cl(V_U)⊂U となるものが存在する．即ち λ∈Λ に対して ∅ ≠ cl(V_{X_λ})⊂X_λ である．このとき V_{X_λ}⊂X_λ は空でない有限集合である．

定理8 AMC ⇔ コンパクトHausdorff空間の直和はパラコンパクトである．

証明 ( ⇒ ) 定理5から明らか．

( ⇐ ) 定理5の証明の X_λ^* はコンパクトHausdorffである．故に同様にしてAMCがわかる．

定理9 AMC ⇔ コンパクトHausdorff空間の直和はメタコンパクトである．

証明定理8と同様．

定理10 AMC ⇔ コンパクトHausdorff空間の直和はPFCSである．

証明定理8と同様．

定義

集合 A に対して ∪A:=∪_x∈Ax と書く．
集合 S が Δ -システム
⇔ ある集合 r が存在して任意の x, y∈S に対して「 x≠y⇒x∩y=r 」．
この集合 r を根と呼ぶ．

補題11 nを正整数，Sをn元集合からなる無限集合とするとき，ある有限部分集合r⊂∪Sが存在して任意の正整数kに対してあるT⊂Sが存在して「|T| = k かつTはrを根とするΔ-システム」となる．

証明 nに関する帰納法．n=1のときは r = ∅ とすればよい．

n>1のとき．x∈Sとm≧0に対して

E₀(x) := { x }
E_m(x) := { y∈S | y∩(∪E_m-1(x)) ≠ ∅ }　(m>0のとき)

とする．Sの同値関係～を

x～y ⇔ ある m≧0 が存在して y∈E_m(x)

で定める．x∈Sの属する同値類を[x]で表すことにする．明らかに，[x]≠[y]のとき x∩y = ∅ である．よってS/～が無限集合のときは r = ∅ とすればよいから，S/～は有限集合であるとする． [x]が無限集合となるようなx∈Sが存在するので，そのようなx∈Sを一つ取る．

(i)任意の有限部分集合z⊂∪[x]に対して，あるy∈[x]が存在して y∩z = ∅ となるとき．任意の正整数kに対してあるT⊂[x]が存在して「|T|=kかつTは∅を根とするΔ-システム」となる．

kに関する帰納法．k=1のときは明らか．

k>1のとき．帰納法の仮定によりT⊂[x]で「|T| = k-1 かつ T は ∅ を根とするΔ-システム」となるものが存在する．T = { y₁, …, y_k-1 } と書く．y₁∪…∪y_k-1⊂∪[x]は有限部分集合だから，あるy_k∈[x]が存在して y_k∩(y₁∪…∪y_k-1) = ∅ である．よって T∪{ y_k } が条件を満たす．

故にr=∅とすればよい．

(ii)ある有限部分集合z⊂∪[x]が存在して，任意のy∈[x]に対してy∩z≠∅となるとき．w⊂zで U := { y∈[x] | y∩z=w } が無限集合となるものを取る．([x]が無限集合だからこのようなwは存在する．)|w|≧1である．A := { y＼w | y∈U } と置く．wの取り方から，Aは(n-|w|)元集合からなる集合である．故に帰納法の仮定から，r₀⊂∪Aが取れる．

r := r₀∪wとする．正整数kを取る．r₀の取り方から，あるB⊂Aが存在して「|B|=kかつBはr₀を根とするΔ-システム」となる．よって T := { b∪w | b∈B } と置けば「|T| = k かつ T は r を根とするΔ-システム」である．

補題12 Aを有限集合からなる無限集合として，kは非負整数，xは∪Aの有限部分集合を動くとする．D(x) := { a∈A | a∩x = ∅ } と置く．Aは「あるk, xに対して|D(x)|≦k」を満たすとして

n₀ := min{ n>0 | あるx, kが存在して|x|=nかつ|D(x)|≦k }

と置き，

k₀∈{ k≧0 | あるxが存在して|x|=n₀かつ|D(x)|≦k }

を一つ取る．このとき S := { x⊂∪A | |x|=n₀, |D(x)|≦ k₀ } は有限集合である．

証明 Sが無限集合であると仮定する．Sに補題1を適用してr⊂∪Sを得る．明らかに|r|<n₀であり，またn₀の最小性からD(r)は無限集合である．T⊂Sをrを根とするΔ-システムとするとき任意のa∈D(r)に対して| { x∈T | x∩a≠∅ } |≦|a| である．

x₁, …, x_m∈{ x∈T | x∩a≠∅ } を互いに異なる元とする．Tの取り方からx_i∩x_j=rである．故にx₁＼r, …, x_m＼rは互いに素である．一方b∈D(r)だからb∩r=∅となる．よって(x_i＼r)∩a=x_i∩a≠∅である．従って((x₁＼r)∩a)∪…∪((x_m＼r)∩a)⊂bからm≦|a|でなければならない．

異なるk₀個の元a₁, …, a_k₀∈D(r)を取る． | ∪_i=1^k₀ { x∈T | x∩a_i≠∅ } | ≦ Σ_i=1^k₀ |a_i| =: M である．N>0を任意に取る．rの取り方により，あるT⊂Sが存在して「|T|=M+NかつTはrを根とするΔ-システム」とできる．T' := T＼∪_i=1^k₀ { x∈T | x∩a_i≠∅ } と置けば |T'|≧N である．a₀∈D(r)＼{ a₁, …, a_k₀ } を一つ取る．

任意のx∈T'を取る．任意の1≦i≦k₀に対して x∩a_i = ∅ となる．またx∈T'⊂Sだから|D(x)|≦ k₀であり，a∩x=∅となるa∈Aは高々k₀個しかない．よってa₀∩x≠∅でなければならない．x∈T'は任意だったから，T'⊂{x∈T| a₀∩x≠∅}である．故にN≦|T'|≦|{x∈T| x∩a₀≠∅}|≦|a₀|となる．N>0は任意だったからa₀が無限集合となり矛盾する．

定義 X を位相空間とする．

X が T₄ 空間
⇔ 互いに素な閉集合 E, F⊂X に対して，ある開集合 U, V⊂X が存在して E⊂U, F⊂V, U∩V= ∅ となる
X がU-空間
⇔ 互いに素な閉集合 E, F⊂X に対してある連続関数 f: X→[0, 1] が存在して f|_E=0, f|_F=1 となる．
X がT-空間
⇔ F⊂X を閉集合， f: F→[0, 1] を連続関数とするとき，ある連続関数 f': X→[0, 1] が存在して f'|_F=f となる．
X がcollectionwise Hausdorff
⇔ F⊂X が離散閉集合ならば， X の互いに素な開集合の族 { U_x }_x∈F が存在して， x∈F に対して x∈U_x となる．
X がcollectionwise T₄
⇔ { F_λ }_λ∈Λ が X の互いに素な閉集合の族ならば， X の互いに素な開集合の族 { U_λ }_λ∈Λ が存在して， λ∈Λ に対して F_λ⊂U_λ となる．

命題13

T-空間はU-空間である．
U-空間はT₄空間である．
パラコンパクトHausdorff空間はT₄空間である．
選択公理 ⇒ T₄空間はU-空間である．(Urysohnの補題)
選択公理 ⇒ T₄空間はT-空間である．(Tietzeの拡張定理)

即ち，選択公理の下ではT₄空間，U-空間，T-空間は同一の概念である．また「T₄空間 ⇒ U-空間」や「T₄空間 ⇒ T-空間」は ZF では証明できないことが知られている．

定理次の命題は( ZF 上)同値．

AMC
T-空間の直和はT-空間である．
T-空間の直和はU-空間である．
T-空間の直和はT₄空間である．
U-空間の直和はU-空間である．
U-空間の直和はT₄空間である．
T₄空間の直和はT₄空間である．
パラコンパクトHausdorff空間の直和はT₄空間である．
collectionwise Hausdorff空間の直和はcollectionwise Hausdorffである．
collectionwise T₄空間の直和はcollectionwise T₄である．
collectionwise T₄空間の直和はT₄空間である．

証明 2⇒3，3⇒4，5⇒6，6⇒4，8⇒7，7⇒6，10⇒11 は明らかだから，1⇒2，1⇒5，1⇒8，4⇒1 と 1⇒9，9⇒1 と 1⇒10，11⇒1 を示せばよい．

(1 ⇒ 2) { (X_λ, O_λ) }_λ∈Λ をT-空間の族として X := $\coprod$ _λ∈ΛX_λ とする． F⊂X を閉集合， f: F→[0, 1] を連続写像とする． F_λ := F∩X_λ, f_λ := f|_{F_λ} とすれば， X_λ がT-空間であることから

A_λ := { g: X_λ→[0, 1] | g|_{F_λ}=f_λ }

は空でない． { A_λ }_λ∈Λ にAMCを適用して空でない有限集合 B_λ⊂A_λ を得る．このとき連続関数 f': X→[0, 1] を x∈X_λ に対して f'(x) := max{ g(x) | g∈B_λ } で定めれば f'|_F=f である．

(4 ⇒ 1) { X_λ }_λ∈Λ を非空集合の族とする．各 X_λ は無限集合としても一般性を失わない． P_fin⁰(X_λ) := { F⊂X_λ | 0 < |F| < ∞ } として

M_λ := { <A, B> | A, B⊂P_fin⁰(X_λ), A, B≠ ∅ 任意のF∈Aと任意のG∈Bに対してF∩G≠ ∅ }

と定義する．このとき f_λ: M_λ→P_fin⁰(X_λ) となる写像の族 (f_λ)_λ∈Λ が存在する．

<A, B>∈M_λ とする．まず A が無限集合だとする．G∈B に対して G∩∪A は ∪A の有限部分集合であり， M_λ の定義から |D(G∩∪A)|≦0 を満たす．よって

n₀ := min{ n > 0 | あるx, kが存在して|x|=nかつ|D(x)|≦k }

が存在する．

k₀ := min{ k≧0 | あるxが存在して|x|=n₀ かつ|D(x)|≦k }

とすれば，補題12により S := { x⊂∪A | |x|=n₀, |D(x)|≦k₀ } は有限集合である．

そこで

f_λ(A, B) := ∪A　(Aが有限集合のとき)
f_λ(A, B) := ∪S　(Aが無限集合のとき)

とすれば f_λ(A, B)∈P_fin⁰(X_λ) である．

a_λ := <0, X_λ>, b_λ := <1, X_λ> として Y_λ := { a_λ, b_λ }∪P_fin⁰(X_λ) と置く． F∈P_fin⁰(X_λ) に対して F^↑ := { G∈P_fin⁰(X_λ) | F⊂G } , F^* := { G∈P_fin⁰(X_λ) | F∩G≠ ∅ } とする． Y_λ の開集合 U⊂Y_λ を次の二条件を満たすものとして定める．

a_λ∈U ならばある F∈P_fin⁰(X_λ) が存在して F^↑⊂U
b_λ∈U ならばある F∈P_fin⁰(X_λ) が存在して F^*⊂U

すると各 Y_λ はT-空間である．

まず Y_λ が位相空間であることを示す．

(i)明らかに ∅ と Y_λ は開集合である．

(ii) 開集合の和集合も明らかに開である．

(iii) U, V を開集合とする． a_λ∈U∩V とする．このとき a_λ∈U, a_λ∈V である．よってある F_U, F_V∈P_fin⁰(X_λ) が存在して F_U^↑⊂U, F_V^↑⊂V となる．このとき F := F_U∪F_V と置けば明らかに F^↑⊂U∩V である．故に U∩V は開集合の定義(1)を満たす．(2)についても同様である．

以上により Y_λ は位相空間である．

Y_λ がT-空間であることを示すため， A⊂Y_λ を閉集合， f: A→[0, 1] を連続写像とする． Y_λ の位相の定義から， y≠a_λ, b_λ のとき { y } ⊂Y_λ が開であることに注意し， f': Y_λ→[0, 1] を以下のように定義すればよい．

(i) a_λ, b_λ ∉ A のとき．

f'(y) := f(y)　(y∈Aのとき)
f'(y) := 0　(y ∉ Aのとき)

と定義すれば f' は連続である．

(ii) a_λ, b_λ∈A のとき．
開近傍 U∋a_λ, V∋b_λ, U∩V= ∅ を取り

f'(y) := f(y)　(y∈Aのとき)
f'(y) := f(a_λ)　(y∈U＼Aのとき)
f'(y) := f(b_λ)　(y∈V＼Aのとき)
f'(y) := 0　(それ以外のとき)

と定義すれば f' は連続である．

(iii) a_λ∈A, b_λ ∉ A のとき．
開近傍 U∋a_λ, V∋b_λ, U∩V= ∅ , V∩A= ∅ を取り

f'(y):= f(y)　(y∈Aのとき)
f'(y):= f(a_λ)　(y∈U＼Aのとき)
f'(y):= 0　(それ以外のとき)

と定義すれば f' は連続である．

(iv) a_λ ∉ A, b_λ∈A のとき．
(iii)と同様．

Y := $\coprod$ _λ∈ΛY_λ と置く．仮定により Y は T₄ 空間である． A := { a_λ | λ∈Λ }, B := { b_λ | λ∈Λ } とすればこれらは Y の閉集合で互いに素である．故に U⊃A, V⊃B, U∩V= ∅ となる開集合 U, V が存在する． A_λ := { F∈P_fin⁰(X_λ) | F^↑⊂U }, B_λ := { F∈P_fin⁰(X_λ) | F^*⊂V } と置くと A_λ≠ ∅, B_λ≠ ∅ で，任意の F∈A_λ と任意の G∈B_λ に対して F∩G≠∅となる．

F∩G=∅ とすると F∈G^* である．よって F^↑∩G^*≠ ∅ となり U∩V= ∅ に矛盾する．

故に <A_λ, B_λ>∈M_λ である．そこで F_λ := f_λ(A_λ, B_λ) と置けばよい．

(1 ⇒ 5) 1⇒2と同様．

(1 ⇒ 7) { (X_λ, O_λ) }_λ∈Λ を T₄ 空間の族として X := $\coprod$ _λ∈ΛX_λ とする． E, F⊂X を互いに素な閉集合とする． E_λ := E∩X_λ, F_λ := F∩X_λ と置けばこれらは X_λ の互いに素な閉集合．よって X_λ が T₄ だから

A_λ := { <U, V>∈O_λ×O_λ | U⊃E_λ, V⊃F_λ, U∩V= ∅ }

は空でない． { A_λ }_λ∈Λ にAMCを適用して空でない有限集合 B_λ⊂A_λ を得る．このとき U_λ := ∩_{<U, V>∈B_λ}U，V_λ := ∩_{<U, V>∈B_λ}V とすれば E_λ⊂U_λ，F_λ⊂V_λ，U_λ∩V_λ= ∅ である．そこで U := ∪_λ∈ΛU_λ∈O, V := ∪_λ∈ΛV_λ∈O とすれば明らかに

U⊃E, V⊃F, U∩V= ∅ .

故に X は T₄ である．

(9 ⇒ 1) 4⇒1 の証明で定義した Y_λ はcollectionwise Hausdorffである．故に仮定11から Y := $\coprod$ _λ∈ΛY_λ はcollectionwise Hausdorffとなる． A, B⊂Y は離散閉集合となるから，4⇒1 と同様にしてAMCを示すことができる．

(11 ⇒ 1) 4⇒1 の証明で定義した Y_λ はcollectionwise T₄ である．故に仮定11から Y := $\coprod$ _λ∈ΛY_λ は T₄ 空間となり，4⇒1 と同様にしてAMCを示すことができる．

命題15 可算選択公理 ⇔ コンパクトな空間の可算直和はLindelöfである．

証明 ( ⇒ ) 明らか．

( ⇐ ) { X_n }_n∈N を非空集合の族とする．離散位相空間 ∪_n∈NX_n の一点コンパクト化を X = { ∞ }∪(∪_n∈NX_n) とする． X はコンパクトだから，仮定より XN=X{ 0 }{ 1 }… はLindelöfである． { X }∪{ { n, x } | n∈N, x∈X_n } は X∪N の開被覆だから，可算部分被覆 { U_n | n∈N } が存在する． n∈N に対して n^* := min{ m∈N | n∈U_m } として U_n^*= { n, x_n } と書けば (x_n)_n∈N∈Π_n∈NX_n である．

定理16 選択公理
⇔ コンパクトな空間の直積はLindelöfである，かつコンパクトな空間の可算直和はLindelöfである．

証明 ( ⇒ ) 明らか．

( ⇐ ) 選択公理が成り立たないと仮定する．非空集合の族 ${X_λ}_{λ∈Λ}$ で $Π_{λ∈Λ}X_λ$ = ∅ となるものが存在する．各 X_λ に密着位相を入れて直和 Y_λ := X_λ∪{ ∞ } を考える． Y_λ はコンパクトだから仮定により Y := Π_λ∈ΛY_λ はLindelöfとなる．π_λ: Y→Y_λ を標準射影とすると， $Π_{λ∈Λ}X_λ$ = ∅ だから { π_λ^-1(∞) | λ∈Λ } は Y の開被覆である． Y がLindelöfだから，可算部分集合 Γ⊂Λ が存在して { π_λ^-1(∞) | λ∈Γ } が Y の開被覆となる．このとき Π_λ∈ΓX_λ= ∅ であるが，一方命題15より可算選択公理が成立するから，矛盾する．

参考文献

Paul Howard, Kyriakos Keremedis, Herman Rubin and Jean E. Rubin, Disjoint Unions of Topological Spaces and Choice, Math. Log. Quart. 44 (1998), 493--508, http://onlinelibrary.wiley.com/doi/10.1002/malq.19980440408/
Horst Herrlich and Kyriakos Keremedis, Topological sums and products in ZF-set theory,Topology and its Applications 156 (2009), 1994--1999,http://www.sciencedirect.com/science/article/pii/S0166864109000960
H. Lauchli, Auswahlaxiom in der Algebra, Comment. Math. Helv. 37 (1963), 1--18
Horst Herrlich, Products of Lindelof T₂ -spaces are Lindelof ― in some models of ZF, Comment. Math. Univ. Carolin. 43,2 (2002), 319--333, http://dml.cz/handle/10338.dmlcz/119322

コメントはまだありません。

位相空間の直積・直和

参考文献

コメント

コメントする