次の命題をKönigの定理という．

命題 { X_λ }_λ∈Λ と { Y_λ }_λ∈Λ が集合族で，各 λ∈Λ に対して |X_λ| < |Y_λ| ならば， |∪_λ∈ΛX_λ| < |Π_λ∈ΛY_λ| である．

定理 次の命題は( ZF 上)同値．

1. 選択公理
2. 各 λ∈Λ に対して |X_λ| < |Y_λ| ならば， |∪X_λ| ≦ |ΠY_λ| である．
3. 各 λ∈Λ に対して |X_λ| < |Y_λ| ならば， |∪X_λ| ≦^* |ΠY_λ| である．
4. 各 λ∈Λ に対して |X_λ| < |Y_λ| ならば， |ΠY_λ| 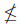^* |∪X_λ| である．
5. 各 λ∈Λ に対して |X_λ| < |Y_λ| ならば， |ΠY_λ| 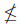|∪X_λ| である．

証明 (1 ⇒ 2) { X_λ }_λ∈Λ, { Y_λ }_λ∈Λ を集合族で，各 λ∈Λ に対して |X_λ| < |Y_λ| を満たすとする． λ≠μ に対して X_λ∩X_μ= ∅ としてよい．

A_λ := { <f, y>∈Y_λ^X_λ×Y_λ | fは単射，y ∉ Im(f) }

と置けば A_λ≠ ∅ である．よって選択公理により (<f_λ, y_λ>)_λ∈Λ∈Π_λ∈ΛA_λ が存在する． μ∈Λ に対して g_μ: ∪X_λ→Y_μ を

g_μ(x) := f_μ(x)　(x∈X_μ のとき)
g_μ(x) := y_μ　(x ∉ X_μ のとき)

と定める．これにより g: ∪X_λ→ΠY_λ が g(x) := (g_λ(x))_λ∈Λ で定まる． g は単射である．

よって |∪X_λ|≦|ΠY_λ| が分かった．

(2 ⇒ 3) |X|≦|Y| ⇒ |X|≦^*|Y| だから明らか．

(3 ⇒ 1) を非空集合の族とする．各 λ∈Λ に対して 1 < |X_λ| としてよい．このとき Y_λ:= { ∅ } とすれば， |Y_λ| = 1 < |X_λ| だから仮定2により 1 = |∪Y_λ|≦^*|ΠX_λ| である．その為には ΠX_λ≠ ∅ でなければならない．

(1 ⇒ 4)全射 f: ∪X_λ→ΠY_λ が存在すると仮定する． π_λ: ΠY_λ→Y_λ を標準全射とすれば写像 g_λ := π_λf|_Xλ: X_λ→Y_λ が得られる．このとき C_λ := Y_λ＼Im(g_λ)≠ ∅ だから選択公理により (y_λ)_λ∈Λ∈Π_λ∈ΛC_λ⊂Π_λ∈ΛY_λ が存在する． f は全射だったから，ある x∈∪X_λ が存在して f(x)=(y_λ)_λ∈Λ となる． x∈X_μ とすれば g_μ(x)=π_μ(f(x))=π_μ((y_λ)_λ∈Λ)=y_μ となり y_μ ∉ Im(g_μ) に矛盾する．

(4 ⇒ 5) |X|^*|Y| ⇒ |X||Y| だから明らか．

(5 ⇒ 1) を非空集合の族とする． λ∈Λ に対して Y_λ:= ∅ とすれば， |Y_λ| = 0 < |X_λ| だから仮定3により |ΠX_λ||∪Y_λ| = 0 である．その為には ΠX_λ≠ ∅ でなければならない．

系 選択公理 ⇔ Konigの定理

証明 前定理の条件2かつ条件5がKönigの定理であるから明らか．

定理 選択公理
⇔ { X_λ }_λ∈Λ が集合族で，各 λ∈Λ に対して 2≦|X_λ| ならば |∪_λ∈ΛX_λ|≦|Π_λ∈ΛX_λ| ．

証明 ( ⇒ ) { X_λ }_λ∈Λ を各 λ∈Λ に対して 2≦|X_λ| なる集合族とする． A_λ:= { <a, b>∈X_λ² | a≠b } と置けば A_λ≠ ∅ である．よって選択公理により (<a_λ, b_λ>)_λ∈Λ∈Π_λ∈ΛA_λ が存在する． μ∈Λ に対して f_μ: ∪X_λ→X_μ を

f_μ(x) := x　(x∈X_μ のとき)
f_μ(x) := a_μ　(x∈X_λ＼{ a_λ }, λ≠μ のとき)
f_μ(x) := b_μ　(x=a_λ, λ≠μ のとき).

と定める．これにより f: ∪X_λ→ΠY_λ が f(x) := (f_λ(x))_λ∈Λ で定まる． f は単射である．よって |∪X_λ|≦|ΠX_λ| が分かった．

( ⇐ ) を非空集合の族とする．各 λ∈Λ に対して 2≦|X_λ| としてよい．このとき 0 < |∪X_λ|≦|ΠX_λ| である．