定義 X を順序集合とする．

1. X が帰納的 ⇔ 任意の部分全順序集合 C⊂X が上界を持つ．
2. X が鎖完備 ⇔ 任意の部分全順序集合 C⊂X が上限を持つ．
3. X が準帰納的 ⇔ 任意の部分整列順序集合 C⊂X が上界を持つ．
4. X が準鎖完備 ⇔ 任意の部分整列順序集合 C⊂X が上限を持つ．
5. x∈X に対して x^↓ := { y∈X | y < x } と置く．

定義 P = 帰納的，鎖完備，準帰納的，準鎖完備，に対して命題 F_i(P) を以下のように定める．

1. F₁(P) ⇔ X が P順序集合で，写像 f: X→X が「任意の x∈X に対して上限 sup{ x, f(x) } が存在する」を満たすならば， φ(x) := sup{ x, f(x) } は不動点を持つ．
2. F₂(P) ⇔ X が P順序集合で，写像 f: X→X が「任意の x∈X に対して x≦f(x) 」を満たすならば， f は不動点を持つ．
3. F₃(P) ⇔ X が P順序集合で，順序を保つ写像 f: X→X が「ある x∈X について x≦f(x) 」を満たすならば， f は不動点を持つ．
4. F₄(P) ⇔ X が P順序集合で，順序を保つ写像 f: X→X が「任意の x∈X について x≦f(x) 」を満たすならば， f は不動点を持つ．

定理 次の命題は( ZF 上)同値．

1. 選択公理
2. P = 帰納的，鎖完備，準帰納的，準鎖完備，に対する F₁(P) ， F₂(P)
3. P = 鎖完備，準鎖完備，に対する F₃(P) ， F₄(P)

証明 「A ならば B」を「A→B」と書くとき，以下は明らかである．

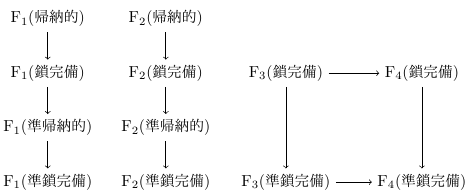
よって以下を示せばよい．

• 選択公理 ⇒ F₁(帰納的)
• F₁(P) ⇒ F₂(P)
• P = 鎖完備，準鎖完備に対する F₂(P) ⇒ F₃(P)
• F₄(準鎖完備) ⇒ 選択公理

(選択公理 ⇒ F₁(帰納的)) Zornの補題により， X は極大元 x∈X を持つ． φ の定義より x≦φ(x) だから， x の極大性から x=φ(x) となり x が φ の不動点である．

(F₁(P) ⇒ F₂(P)) x≦f(x) だから， sup{ x, f(x) } = f(x) は存在する．よって F₁(P) より φ(x) := sup{ x, f(x) } が不動点 y を持つ．このとき y = φ(y) = sup{ y, f(y) } = f(y) だから y は f の不動点である．

(F₂(鎖完備) ⇒ F₃(鎖完備)) A := { x∈X | x≦f(x) } と置く． f が順序を保つので， x≦f(x) ならば f(x)≦f(f(x)) ，故に f|_A: A→A となる．部分全順序 W⊂A を取る． X が鎖完備だから上限 s = sup(W)∈X が存在する．任意の w∈W を取る． w≦s だから f(w)≦f(s) である． w∈A だったから w≦f(w)≦f(s) となる．即ち，任意の w∈W に対して w≦f(s) である．故に上限の定義から s≦f(s) となり s∈A である．即ち W⊂A は A の中に上界を持つことが分かった．よって仮定 F₂(鎖完備)から f|_A は不動点を持つ．

(F₂(準鎖完備) ⇒ F₃(準鎖完備)) 同様．

(F₄(準鎖完備) ⇒ 選択公理) 整列可能定理を示す．任意の集合 S を取る．

X := { <T, ≦_T> | T⊂S, ≦_TはTの整列順序 }

と置く． X に順序 ≦ を

<T, ≦_T> < <U, ≦_U> ⇔ あるu∈Uが存在して<T, ≦_T> = <u^↓, ≦_U|_u^↓>

と定める． <X, ≦> は準鎖完備順序集合である．直積 Y := X×N に辞書式順序を入れ，写像 f: Y→Y を f(T, n) := <T, n+1> で定める． f は明らかに不動点を持たず， y∈Y に対して y≦f(y) を満たす．よって仮定より Y は準鎖完備でない．故に部分整列順序集合 W⊂Y で上限を持たないものが存在する．このとき W₁ := { T | <T, n>∈W }⊂X は部分整列順序集合である．故に上限 T = sup(W₁)∈X を持つ．

T⊊S と仮定する．

(i) T∈W₁ のとき
s∈S＼T を取り， T に s を最大元として付け加えた順序集合を T⁺ とする．このとき T⁺∈X で，明らかに <T⁺, 0> = sup(W) となり矛盾する．

(ii) T ∉ W₁ のとき
明らかに <T, 0> = sup(W) となり矛盾する．

(i)(ii)より T=S が分かり， S は整列可能である．