定義 Xを位相空間とする．

1. X の開集合全体のなす集合を O_X で表す．
2. X の閉集合全体のなす集合を A_X で表す．

3. X がコンパクト
   ⇔ 部分集合 U(≠ ∅ )⊂O_X が X=∪U を満たすならば，ある非負整数nとあるU₀, …, U_n∈Uが存在して X=U₀∪…∪U_n．

   集合Aに対して ∪A := ∪_B∈A B, ∩A := ∩_B∈A B である．

4. B⊂O_X が基底
   ⇔ 任意の開集合U∈O_Xに対してある部分集合C⊂Bが存在して U = ∪C と書ける．
5. F⊂A_X が有限交差性(finite intersection property)を持つ
   ⇔ 任意の非負整数nと任意のF₀, …, F_n∈Fに対してF₀∩…∩F_n≠∅．

コンパクトという条件を考えるときには，開集合は基底の元のみを考えればよい．即ち，次の補題が成り立つ．

補題1 B を位相空間 X の基底とするとき，
X がコンパクト
⇔ 部分集合U⊂B が X=∪U を満たすならば，ある非負整数nとあるU₀, …, U_n∈Uが存在して X=U₀∪…∪U_n．

証明⇒は明らか．逆←を示す．

U⊂O_X が X=∪U を満たすとする．U∈U に対して B_U := { V∈B | V⊂U } と置けば，B が基底であることから U = ∪B_U が分かる．よってV := ∪_U∈U B_U⊂B と置けば X = ∪_U∈U U = ∪_U∈U∪_V∈BU V = ∪_V∈V V だから，仮定によりある V₀, …, V_n∈V が存在して X = V₀∪…∪V_n である．このとき各 0≦i≦n について V_i∈B_Ui となる U_i∈U を取れば X = U₀∪…∪U_n である．

定義 X を位相空間とする．

1. A⊂O_X がX上admissible
   ⇔ 任意の非負整数nと任意のU₀, …, U_n∈Aに対してU₀∪…∪ U_n≠ X．
2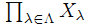. X=を直積位相空間とするとき

   B(X) := { Π_λ∈Λ U_λ | U_λ∈O_X, 有限個のλ∈Λを除いて U_λ = X_λ }

   と置く．B(X)はXの基底である．

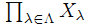3. X=を直積位相空間とするとき， 標準射影X→X_λをπ_Xλで表す．π_Xλは連続である．

補題2 位相空間Xに対して次の命題は同値．

1. X がコンパクト
2. A⊂O_X がX上admissible ⇒ ∪A≠X

証明 対偶を考えればよい．

補題1を踏まれば，条件2では A⊂B としてよいことが分かる．

補題3 Xをコンパクト位相空間，Yを位相空間とし，A⊂B(X×Y) は X×Y 上admissibleとする．x∈Xに対して A_x := { U∈A | x∈π_X(U) } と置く．このときある点x∈Xが存在してπ_Y(A_x) := { π_Y(U) | U∈A_X } はY上admissibleとなる．そのような点 x∈X 全体からなる集合を C(A) と書くと，C(A)⊂X は空でない閉集合である．

証明 A⊂B(X×Y) を X×Y 上admissibleとする．

C :=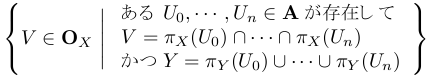

と定めると，CはX上admissibleである．

故にXのコンパクト性からX≠∪Cである．x∈X＼∪Cを任意に一つ取ると {π_Y(U) | U∈A_x } はY上admissibleである．

任意のπ_Y(U₀), …, π_Y(U_n)　(U_i∈A_x)を取る．V := π_X(U₀)∩…∩π_X(U_n)と置く．U_i∈A_xだから x∈π_X(U_i)，故にx∈Vである．一方xの取り方により V ∉ C でなければならない．よって Y≠π_Y(U₀)∪…∪π_Y(U_n) が分かる．

x∈Xは任意だったからX＼∪B⊂C(A)である．X＼∪B ⊊ C(A)と仮定する．x∈C(A)＼(X＼∪C) = C(A)∩∪C が存在する．x∈V となる V∈B を取る． Cの定義から，あるU₀, …, U_n∈Aが存在して

V=π_X(U₀)∩…∩π_X(U_n), Y=π_Y(U₀)∪…∪π_Y(U_n)

と書ける．すると明らかにU₀, …, U_n∈A_Xであるから，{π_Y(U) | U∈A_X } がY上admissibleであることに矛盾する．故にC(A) = X＼∪C⊂X で，これは空でない閉集合である．

定理 をコンパクト位相空間の族とする．Λは整列可能で，∪_λ∈Λ(A_Xλ＼{ ∅ })は選択関数 f を持つとする．このとき直積位相空間もコンパクトである．

証明 A⊂B(ΠX_λ)をΠX_λ上admissibleとする．補題2の条件2からΠX_λ≠∪Aを示せばよい．その為に元y∈(Π X_λ)＼∪Aの存在を示す．存在が仮定されている選択関数fを一つ取っておく．

仮定によりΛは整列可能だから，Λは順序数であるとしてよい．|Λ|=|Λ+1|だから，Λは後続型順序数としてよい．そこで順序数νを使ってΛ=ν+1と書く．同様にして，νも後続型順序数としてよい．α≦νに対してY_α := Π_α≦β≦ν X_βと置く．Y_α = X_α×Y_α+1 である．α<νに対して，帰納的に次を満たすx_α∈X_αが取れることを示す．

α≦νに対してA_α := { U∈A | 任意のβ<αに対してx_β∈π_Xβ(U) } と定義する．
このときα<νに対してπ_Yα+1(A_α+1)はY_α+1上admissible

(i) α=0のとき．
A₀=A と Y₀=X₀× Y₁ に補題3を適用して空でない閉集合 C₀ := C(A)⊂X₀ を得る． x₀ := f(C₀) とすれば

A₁ = { U∈A | 任意のβ<1に対してx_β∈π_Xβ(U) } = { U∈A | x₀∈π_X0(U) }

だから，C₀の取り方によりπ_Y1(A₁)はY₁上admissibleである．

(ii) α=β+1のとき．
β<αだから，帰納法の仮定によりπ_Yβ+1(A_β+1)はY_β+1上admissibleである．今β+1=αだから，π_Yα(A_α)はY_α上admissibleとなる．π_Yα(A_α) と Y_α=X_α×Y_α+1 に補題3を適用して空でない閉集合 C_α := C(π_Yα(A_α))⊂X_α を得る．x_α := f(C_α)とすれば

A_α+1
= { U∈A | 任意のβ<α+1に対してx_β∈π_Xβ(U) }
= { U∈A | 任意のβ<α に対してx_β∈π_Xβ(U) } ∩ { U∈A | x_α∈π_Xα(U) }
= A_α∩{ U∈A | x_α∈π_Xα(U) }
= { U∈A_α | x_α∈π_Xα(U) }

だからπ_Xαπ_Yα=π_Xαに気をつけると

π_Yα(A_α+1)
= {π_Yα(U) | U∈A_α, x_α∈π_Xα(U) }
= {π_Yα(U) | U∈A_α, x_α∈π_Xα(π_Yα(U)) }
= { U∈π_Yα(A_α) | x_α∈π_Xα(U) }

である．よって C_α の取り方によりπ_Yα+1(π_Yα(A_α+1)) はY_α+1上admissibleである．今π_Yα+1π_Yα=π_Yα+1だから，π_Yα+1(A_α+1)はY_α+1上admissibleであることが分かった．

(iii) αが極限順序数のとき．
帰納法の仮定により，任意のβ<αに対してπ_Yβ+1(A_β+1)はY_β+1上admissibleである．定義から明らかにA_α⊂A_β+1である．よってπ_Yβ+1(A_α)はY_β+1上admissibleとなる．π_Yα(A_α)はY_α上admissibleである．

そこでπ_Yα(A_α)とY_α=X_α× Y_α+1に補題3を適用して空でない閉集合 C_α := C(π_Yα(A_α))⊂X_α を得る．x_α := f(C_α) とすれば(ii)のときと同様にしてπ_Yα+1(A_α+1)はY_α+1上admissibleであることが分かる．

(i) (ii) (iii)によりx_α∈ X_α (α<ν)が取れた．今νは後続型だったから，α+1=νとなるα<νを取るとπ_Xα+1(A_α+1)はY_α+1上admissible，即ちπ_Xν(A_ν)はY_ν=X_ν上admissibleである．よってX_νがコンパクトだから C := X_μ＼∪_U∈Aμπ_Xμ(U) は空でない閉集合．x_ν := f(C) と置く．このときy=(x_α)_α≦ν∈Y₀はy ∉∪Aを満たす．

あるU∈Aが存在してy∈ Uとなったとする．勿論任意のα≦νに対してx_α∈π_Xα(U)である．x_ν=f(C)∈ C=X＼∪_U∈Aνπ_Xν(U)だからU∉A_νでなければならない．従ってあるα<νが存在してx_α∉π_Xα(U)となり，x_αの取り方に矛盾する．

系 選択公理 ⇒ Tychonoffの定理

系 選択公理を使わずに次が証明できる．

1. [0, 1]^N はコンパクトである．
2. n∈Nに対して | X_n | = 2 のとき Π_n∈N X_n はコンパクト
3. p進整数環 Z_p はコンパクトである．

証明 (1) Nは整列可能である．A_{[0, 1]}＼{ ∅ } は選択関数を持つ．

f: A_{[0, 1]}＼{ ∅ }→[0, 1] を f(F) := min F で定めればよい．(Fは有界な空でない閉集合だから，最小値を持つ．)

故に定理から [0, 1]^N はコンパクトであることが分かる．

(2) | X_n | = 2 だから「A∈∪_n∈N(A_Xn＼{ ∅ })で |A|≧2 となるもの」は A=X_n しかない．故に { X_n }_n∈N の選択関数が存在すれば∪_n∈N(A_Xn＼{ ∅ })も選択関数を持つ事が分かる．

(i) { X_n }_n∈N の選択関数があるとき，Nは整列可能だからよい．

(ii) { X_n }_n∈N の選択関数がないとき，このとき Π_n∈N X_n = ∅ はコンパクトである．

(3) Z_p⊂Π_n∈NZ/pⁿZ$は閉部分集合である． (1)と同様にしてΠ_n∈NZ/pⁿZはコンパクトだから，閉部分集合Z_pもコンパクトである．

この | X_n | = 2 を | X_n | = 3 に変えた命題，即ち「n∈Nに対して| X_n | = 3 のとき Π_n∈N X_n はコンパクト」は選択公理無しには証明できない．何故ならば，次の定理が成立するからである．

定理正整数mに対して，次が成り立つ．

n∈N に対して 0<| X_n |≦m のとき { X_n }_n∈N は選択関数を持つ．
⇔ n∈N に対して | X_n |≦m+1 のとき Π_n∈N X_nはコンパクト

証明(⇒) { X_n }_n∈Nが | X_n |≦m+1 を満たすとする．

(i) { X_n }_n∈N の選択関数がないとき．
このときはΠ_n∈NX_n= ∅ はコンパクトである．

(ii) { X_n }_n∈N の選択関数があるとき．
∪_n∈N(A_Xn＼{ ∅ , X_n })の元 A は 0<|A|≦m を満たす．よって∪_n∈N(A_Xn＼{ ∅ , X_n })は選択関数を持つ．{ X_n }_n∈Nの選択関数とあわせれば∪_n∈N(A_Xn＼{ ∅ })が選択関数を持つ事が分かる．勿論添え字集合Nは整列可能だから，定理によりΠ_n∈NX_nはコンパクトである．

(←) 通常の「Tychonoffの定理⇒選択公理」の証明と同様にしてできる．

次の命題をBPI (Boolean Prime Ideal Theorem)という．

命題 [BPI]任意のブール代数は素イデアルを持つ．

命題 選択公理 ⇒ BPI

命題 BPIを仮定すると，以下が成り立つ．

1. B がブール代数で F⊂B が有限交差性を持つとき，超フィルター U⊂B で U⊃F となるものが存在する．
2. 位相空間 X がコンパクト ⇔ 任意の超フィルター U⊂P(X) が収束する．

定理 選択公理 ⇒ Tychonoffの定理

証明 をコンパクト位相空間の族として， X := とする． F⊂A_X が有限交差性を持つとする．このときBPIにより，超フィルター U⊂P(X) で U⊃F となるものが存在する．

U_λ:= { π_Xλ(Y) | Y∈U } ⊂P(X_λ) は超フィルターである．よって X_λ のコンパクト性とBPIから， C_λ:= { x∈X_λ | U_λ が x に収束する } ≠ ∅ である．従って選択公理により元 x=(x_λ)_λ∈Λ∈Π_λ∈ΛC_λ⊂X が取れる．このとき x の任意の開近傍 U⊂X に対して U∈U である．

今， F∈F が x ∉ F を満たすと仮定する．すると X＼F∋x は x の開近傍であり，よって X＼F∈U である． F∈F⊂U だったから ∅ =F∩(X＼F)∈U となり矛盾する．故に任意の F∈F に対して x∈F ，即ち x∈∩F であり， X がコンパクトであることが分かった．

系 BPI⇒ コンパクトHausdorff空間の直積はコンパクト．

証明 先の証明で選択公理を使っている部分は三箇所ある．一つ目、二つ目はBPIを使っているところだから，BPIがあればよい．三つ目は x_λ∈C_λ を取る所であるが，今 X_λ はHausdorffと仮定しているから，収束先は一意に定まる．故に選択公理を使わずに x_λ を取ることができる．