定義 Xを位相空間とする．

1. X の開集合全体のなす集合を O_X で表す．
2. X の閉集合全体のなす集合を A_X で表す．

3. X がコンパクト
   ⇔ 部分集合 U(≠ ∅ )⊂O_X が X=∪U を満たすならば，ある非負整数nとあるU₀, …, U_n∈Uが存在して X=U₀∪…∪U_n．

   集合Aに対して ∪A := ∪_B∈A B, ∩A := ∩_B∈A B である．

4. F⊂A_X が有限交差性(finite intersection property)を持つ
   ⇔ 任意の非負整数nと任意のF₀, …, F_n∈Fに対してF₀∩…∩F_n≠∅．

補題1 位相空間Xに対して次の命題は同値．

1. X がコンパクト
2. F⊂A_X が有限交差性を持つ ⇒ ∩F≠ ∅

定義 X を位相空間とする．

1. (I, ≦) を有向集合とするとき， { x_i }_i∈I (x_i∈X) を X の有向点列という．
2. x∈X が X の有向点列 { x_i }_i∈I の集積点(cluster point)
   ⇔ x の任意の開近傍 U⊂X と任意の i∈I に対して，ある j≧i が存在して x_j∈U となる．
3. X の有向点列 { x_i }_i∈I が x∈X に収束する
   ⇔ x の任意の開近傍 U⊂X に対してある i∈I が存在して，任意の j≧i に対して x_j∈U となる．

定義 (I, ≦), (J, ≦) を有向集合とし， { x_i }_i∈I を X の有向点列とする．順序を保つ写像 i: J→I が「任意の i₀∈I に対してある j∈J が存在して i₀≦i(j) 」を満たすとき，有向点列 { x_i(j) }_j∈J を { x_i }_i∈I の部分有向点列という．

命題 X を位相空間とする．

1. x∈X が X の有向点列 { x_i }_i∈I の集積点である
   ⇔ x に収束する { x_i }_i∈I の部分有向点列が存在する．
2. X がコンパクト
   ⇔ X の任意の有向点列が集積点を持つ．
   ⇔ X の任意の有向点列が収束する部分有向点列を持つ．

定理以下の命題は(ZF上)同値．

1. 選択公理
2. コンパクト空間の直積はコンパクト　(Tychonoffの定理)
3. コンパクトなT₁空間の直積はコンパクト
4. 開集合が有限個な空間の直積はコンパクト
5. 開集合が丁度3個な空間の直積はコンパクト

証明(1⇒2) をコンパクト空間の族とする． X := がコンパクトであることを示すために， X の有向点列 ξ= { f_i | i∈I } を取る． Σ⊂Λ に対して ξ|_Σ:= { f_i|_Σ | i∈I } と書く．(各 f_i∈X は写像であることに注意しておく．)

A:= { g | Σ⊂Λ, g∈Π_λ∈ΣX_λ, g は ξ|_Σ の集積点 }

と定義し， A に包含関係 ⊂ で順序を入れる． A にZornの補題を適用する為に，部分全順序 C⊂A を取る． h := ∪_g∈Cg ， Σ := ∪_g∈Cdom(g) と置く． h∈Π_λ∈ΣX_λ は ξ|_Σ の集積点である．

故に h∈A となるから， h が C の上界である．従ってZornの補題により A の極大元 g が存在する．

Σ := dom(g)⊊Λ と仮定する． μ∈Λ＼Σ を取る． g は ξ|_Σ の集積点だから， g に収束する部分有向点列 η= { f_φ(j) | j∈J } が存在する．このとき η(μ):= { f_φ(j)(μ) | j∈J } は X_μ の有向点列である．今 X_μ はコンパクトだったから， η(μ) の集積点 a∈X_μ が存在する．このとき Σ' := Σ∪{ μ } として g'∈Π_λ∈Σ' X_λ を

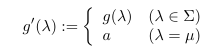
と定めれば g'∈A である．

よって g'⊋g だから g の極大性に矛盾する．故に dom(g)=Λ であり， g は ξ の集積点である．

(2⇒3) 明らか

(3⇒1) を非空集合の族とする．どのX_λにも含まれない元∞ ∉ を用意し，Y_λ := X_λ∪{∞} とする．各Y_λの位相を

O_Yλ := { U⊂Y_λ | Y_λ＼U は有限集合 }∪{ ∅, {∞} }

で定義する．各(Y_λ, O_Yλ)はコンパクトである．

{ U_i }_i∈IをY_λの開被覆とする．O_Yλの定義から，Y_λ＼ U_i0が有限集合となるようなi₀∈Iが存在する．Y_λ＼U_i0 = { y₁, …, y_n } と書く．{U_i}_i∈Iが開被覆であることからy_k∈U_ikとなるi_kが存在する．この時 Y_λ = U_i0∪U_i1∪…∪U_in．従ってY_λはコンパクト．

また明らかにY_λはT₁空間でもある． 故に仮定3から直積空間 Y := Π_λ∈ΛY_λもコンパクトである． O_Yλの定義から，X_λ=Y_λ＼{∞}⊂ Y_λは閉集合． 閉集合の族 {π_λ^-1(X_λ) }_λ∈Λは有限交差性をもつ．

任意のλ₁, …, λ_n∈Λに対し π_λ1^-1(X_λ1)∩…∩π_λn^-1(X_λn)≠ ∅ となることを示せばよい．各X_λは空でないから，x_λ1∈X_λ1, …, x_λn∈X_λn が取れる．λ_i以外のλ∈Λに対しては x_λ := ∞として x := (x_λ)∈Yを考える．明らかにπ_λi(x)∈X_λiだからx∈π_λ1^-1(X_λ1)∩…∩π_λn^-1(X_λn)．

よって補題1から ∅ ≠∩_λ∈Λπ_λ^-1(X_λ)=である．

(2⇒4) 開集合が有限個の空間はコンパクトなので明らか．

(4⇒5) 明らか．

(5⇒1) 3⇒1の証明において，Y_λの位相を

O_Yλ := { ∅ , {∞}, Y_λ }

で定めればよい．

定理 任意の整数n≧3に対して

選択公理 ⇔ 開集合が丁度 n 個な空間の直積はコンパクト

証明 Y_λ := X_λ∪N (disjoint union)として

O_Yλ := { ∅ , N, Y_λ, {4}, {4, 5}, …, {4, 5, …, n} }

と定めればよい．

定理任意の整数n≧3に対して，以下の命題は(ZF上)同値．

1. 選択公理
2. 互いに同相なコンパクト空間の直積はコンパクト
3. 互いに同相な，開集合が丁度n個ある空間の直積はコンパクト

証明 1⇒2 と 2⇒3 は明らか．

(3⇒1) 選択公理は

非空集合の族で全てのX_λの濃度が等しいもの，に対して≠∅ .

と同値だった(集合に関する命題を参照)ことから明らか．

しかし，直接選択公理を示すことも出来るので，その証明を書いておく．簡単のためn=3とする．を互いに素な非空集合の族とする．

, Y := X×N^XとしてYの位相O_λを

O_λ := { ∅, Y, (X＼ X_λ)×N^X }

で定める． λ, μ∈Λとすると|X_λ×N^X|=|X_μ×N^X|である．

そこで，全単射 F: X_λ×N^X→X_μ×N^X により 写像 G: (Y, O_λ)→ (Y, O_μ)を

x∈X_λのとき　G(x, f) := F(x, f)
x∈X_μのとき　G(x, f) := F^-1(x, f)
それ以外のとき　G(x, f) := (x, f)

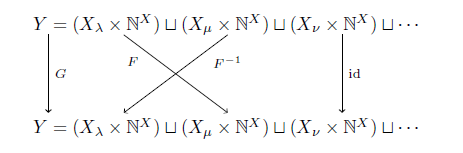
と定める．するとGは同相写像である．故に族 { (Y, O_λ) }_λ∈Λ は仮定3の条件を満たすのでΠ_λ∈Λ(Y, O_λ)はコンパクトである．閉集合の族 {π_λ^-1(X_λ×N^X)}_λ∈Λは有限交差性を持つから，

∅ ≠∩_λ∈Λπ_λ^-1(X_λ×N^X)=×N^X

故に≠ ∅ である．

「コンパクトHausdorff空間の直積はコンパクト」は選択公理と同値でないことが知られている． (BPI (= Boolean Prime Ideal Theorem)と同値である．)