次の命題の証明は順序数・濃度の簡単なまとめを参照．

命題1 濃度 κ, λ≧2 に対し κ+λ≦κ・λ ．

命題2 任意のアレフ に対して ²= ．

命題3 濃度 κ, λ, μ とアレフ が κ・≦λ+μ を満たすとき， κ≦λ または ≦μ となる．

ある自然数 n と全単射 X→n が存在するとき， X を有限集合といい，有限集合でない集合を無限集合という．このように，通常無限集合は「有限集合でない」と定義されるが，では無限集合を直接定義することはできるであろうか．そうして考えられたのがDedekind無限集合である．

定義 X を集合とする．

1. X がDedekind無限 ⇔ |Y| = |X| となる真部分集合 Y ⊊ X が存在する．
2. X がDedekind有限 ⇔ X がDedekind無限でない．

明らかにDedekind無限集合は無限集合(即ち有限集合はDedekind有限)だから，逆に無限集合はDedekind無限(即ちDedekind有限集合はは有限集合)であることを示したいが，実はこれには選択公理を使わなければいけないことが知られている．

命題4 集合 X に対して次の条件は(ZF上)同値．

1. X はDedekind無限集合．
2. 全射でない単射 X→X が存在する．
3. ₀≦|X|．
4. 単射 N→X が存在する．
5. X は可算無限部分集合を持つ．
6. |X| = |X|+₀．
7. |X| = |X|+1．

証明 1⇔2 と 3⇔4⇔5 は明らか．

(2⇒4) f: X→X を全射でない単射とする．全射でないから x∈X＼f(X) が取れる．このとき g: N→X を

g(n) := x　(n=0のとき)
g(n) := f(g(n-1))　(n > 0のとき)

で定義すればこれは単射である．

(5⇒6) Y⊂X を可算無限部分集合とする．|Y| = |Y|+₀ だから

|X| = |(X＼Y)∪Y| = |X＼Y|+|Y| = |X＼Y|+|Y|+₀ = |X|+₀.

(6⇒7) ₀ = ₀+1 だから

|X| = |X|+₀ = |X|+₀+1 = |X|+1.

(7⇒1) X に含まれない元 ∞ を一つ取る． |X| = |X|+1 より全単射 f: X∪{∞}→X が存在する．このとき f(X) ⊊ X かつ |f(X)| = |X| である．

命題5 選択公理を仮定する．無限集合はDedekind無限である．

証明 整列可能定理を使えば明らか．

直接示すには「選択公理 ⇒ 整列可能定理」の証明を真似ればよい． X を無限集合とする．選択公理により P(X)＼{ ∅ } の選択関数 g が存在する．このとき f: N→X を帰納的に f(n) := g(X＼{ f(0), f(1), …, f(n-1) }) で定義すれば f は単射である．

実はこれは可算選択公理があれば証明できる．

命題6 可算選択公理を仮定する．無限集合はDedekind無限である．

証明 X を無限集合とする．命題4により可算無限部分集合 Y⊂X の存在を示せばよい． n≧0 に対して X_n := { <x₀, x₁, …, x_n>∈Xⁿ⁺¹ | i≠j ならば x_i≠x_j } と置く． X が無限集合だから X_n≠ ∅ である．そこで集合族 { X_n }_n=0^∞ に可算選択公理を適用して選択関数 φ: N→∪_n=0^∞X_n を得る． φ(n)∈X_n⊂Xⁿ だから φ(n) = <x₀⁽ⁿ⁾, x₁⁽ⁿ⁾, …, x_n⁽ⁿ⁾> と書ける． Y := { x_i⁽ⁿ⁾ | i≦n } と置けば，{ <i, n>∈N×N | i≦n } は可算無限集合だから Y は高々可算集合である．しかし X_n の定義から明らかに Y は無限集合である．従って Y⊂X は可算無限部分集合である．

命題7 |X| < |Y| かつ |Y|≦^*|X| となるような無限集合 X, Y は存在しない
⇒ 無限集合はDedekind無限集合

証明 A をDedekind有限な無限集合とする． A_n := { <a₀, a₁, …, a_n>∈Aⁿ⁺¹|i≠j ならば x_i≠x_j } と置いて X := ∪_n=0^∞A_n, Y := X∪{ ∅ } と置く．明らかに |X|≦|Y|, |Y|≦^*|X| である．従って |X|≠|Y| を示せばよい．

A がDedekind有限であることから Y もDedekind有限集合である．明らかに |Y| = |X|+1 で，また命題4により |Y|≠|Y|+1 である．よって |X|≠|Y| である．

Dedekind有限以外にも，有限の定義は色々考えられている．

定義 X を集合とする．

1. X が I-finite ⇔ 任意の ∅≠F⊂P(X) が極大元を持つ．
2. X が II-finite ⇔ 任意の部分全順序 ∅≠C⊂P(X) が最大元を持つ．
3. X が III-finite ⇔ P(X) がDedekind有限．
4. X が IV-finite ⇔ X がDedekind有限．
5. X が V-finite ⇔ |X|=0 または 2|X| > |X|．
6. X が VI-finite ⇔ |X|≦1 または |X|² > |X|．
7. X が VII-finite ⇔ X が整列可能でないまたは |N|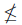|X|．

定義 P(J, K) で次の命題を表す: 任意の X に対して「X が J-finite ⇒ X が K-finite」．

命題8 任意の X に対して「X が有限集合 ⇔ X がI-finite」．

証明 ( ⇒ ) 明らか．

( ⇐ ) X をI-finiteとすると， P_fin(X)⊂P(X) が極大元 Y を持つ．このとき極大性から明らかに Y=X だから X は有限集合である．

命題9 J < K ならば P(J, K) である．

証明 (I-finite ⇒ II-finite) 明らか

(II-finite ⇒ III-finite) 明らか

(III-finite ⇒ IV-finite) 単射 X→P(X) が存在するから明らか．

(IV-finite ⇒ V-finite) X がV-finiteでないとする． |X| > 0 かつ 2|X|=|X| だから X はDedekind無限である，即ちIV-finiteでない．

(V-finite ⇒ VI-finite) X をV-finiteとする． |X| > 1 ならば |X| < 2|X|≦|X|² だからVI-finiteである． |X|≦1 ならば定義からVI-finiteである．

(VI-finite ⇒ VII-finite) X をVI-finiteとする． |X|≦1 ならば |N||X| だからVII-finiteである． |X|² > |X| ならば X は整列可能でない(命題2を参照)からVII-finiteである．

命題10 J < K ならば P(L, J)⇒P(L, K) である．

証明 明らか．

定理11 選択公理 ⇒ P(VII, I) である．従って選択公理の下ではI-finiteからVII-finiteまでの定義は全て同値である．

証明 明らか．

定理12 選択公理 ⇔ P(VII, VI)

証明 ( ⇒ ) 明らか．

( ⇐ ) X を無限集合とする． |X^N| > 1 かつ |X^N|² = |X^N| だから X^N はVI-finiteでない．故にVII-finiteではないが， |N|≦|X^N| だから X^N は整列可能である．故に X も整列可能である．

系 次の命題は( ZF 上)同値．

1. 選択公理
2. P(VII, I)
3. P(VII, II)
4. P(VII, III)
5. P(VII, IV)
6. P(VII, V)

定理13 選択公理 ⇔ P(VI, V)

証明 ( ⇒ ) 明らか．

( ⇐ ) κ を無限基数として λ:=κ・₀+(κ・₀)^* とすれば 2λ=λ である．故に仮定から λ²=λ となる．従って

λ = λ² = (κ・₀)²+2κ・₀・(κ・₀)^*+((κ・₀)^*)²≧κ・₀・(κ・₀)^*

より κ・₀・(κ・₀)^*≦(κ・₀)^*+κ・₀ が分かる．故に命題3から κ・₀≦(κ・₀)^* または (κ・₀)^*≦κ・₀ となる． (κ・₀)^*κ・₀ となるから κ≦κ・₀≦(κ・₀)^* である．

系 次の命題は( ZF 上)同値．

1. 選択公理
2. P(VI, I)
3. P(VI, II)
4. P(VI, III)
5. P(VI, IV)

以上で得られた選択公理と同値な P(J, K) を言い換えると，次の系が得られる．

系 次の命題は( ZF 上)同値．

1. 選択公理
2. P(X) がDedekind無限ならば X は整列可能である． ( P(VII, III) )
3. Dedekind無限集合は整列可能である． ( P(VII, IV) )
4. 2|X|=|X| ならば X は整列可能である． ( P(VII, V) )
5. |X|² = |X| ならば X は整列可能である． ( P(VII, VI) )
6. P(X) がDedekind無限ならば |X|² = |X|． ( P(VI, III) )
7. Dedekind無限集合 X に対して |X|² = |X|． ( P(VI, IV) )
8. 無限集合 X に対して， 2|X| = |X| ⇒ |X|² = |X|． ( P(VI, V) )

定義 X を集合とする．

1. X がD-finite ⇔ |X|≦1 であるか，ある A, B が存在して |A| < |X| かつ |B| < |X| かつ X = A∪B．
2. X がamorphous ⇔ X = A∪B ( A, B は互いに素な無限集合)と書けない．

命題14 P(IV, D) である．

証明 X をIV-finite，即ちDedekind有限とする． |X|≦1 ならばD-finiteであるから |X| > 1 とする． x∈X を一つ取れば， X がDedekind有限だから |X＼{ x }| < |X| である．故に |X＼{ x }| < |X|，|x| < |X|， X = (X＼{ x })∪{ x } と書けるのでD-finiteである．

命題15 P(D, VII) である．

証明 X をD-finiteとする． |X|≦1 ならばVII-finiteである． |X| > 1 の場合は明らかに X は整列不可能であるからVII-finiteである．

命題16 X が有限集合 ⇒ X はamorphous．

証明 明らか．

命題17 X がamorphous ⇒ X はII-finite．

証明 X をII-finiteでない集合とすると，最大元を持たない部分全順序 ∅ ≠C⊂P(X) が存在する．

(i)無限集合 Y∈C が存在する場合
このとき X＼Y も無限集合で X=(X＼Y)∪Y だから， X はamorphousである．

(ii)任意の Y∈C が有限集合の場合
C は最大元を持たないから C= { F_n | n∈N } ， n < m ならば F_n⊊F_m ，と書けることが分かる． G₀ := F₀，G_n+1 := F_n+1＼F_n として

A := ∪_n∈NG_2n
B := ∪_n∈NG_2n+1

とすれば A, B は互いに素な無限集合で X = A∪B である．

定理18 次の命題は( ZF 上)同値．

1. 選択公理
2. κ・λ=κ+λ ．
3. κ+λ=κ または κ+λ=λ ．

証明 濃度の性質を参照．

定理19 選択公理 ⇔ P(D, I)

証明 ( ⇒ ) 定理18の3より明らか．

( ⇐ ) 定理18の3を示す． κ=|X|, λ=|Y| を任意の無限濃度とすれば X∪Y が無限集合だから |X|=|X∪Y| または |Y|=|X∪Y| となる．

定理20 選択公理
⇔「X が有限集合 ⇔ |X|≦1 であるか，ある Y が存在して |X|+|Y| < |X|・|Y|．」

証明 ( ⇒ ) 定理18の2より明らか．

( ⇐ ) 定理18の2を示す． κ=|X|, λ=|Y| を任意の無限濃度とすれば X が無限集合だから命題1より |X|+|Y|=|X|・|Y| となる．

最後に，命題「無限集合はDedekind無限集合である」と同値な命題を述べておく．その為にまず補題を一つ示す．

補題21 集合 X に対して ₀≦^* |X| ⇔ ₀≦P(X) である．

証明 ( ⇒ ) f: X→N を全射とする．このとき f^-1: N→P(X) は単射である．

( ⇐ ) f: N→P(X) を単射とする． g: N→P(X) を以下のように帰納的に定義する． n≧0 とする． 0≦m ≦n-1 に対し g(m) が

| { f(k)＼∪_{m < n}g(m) | k≧n } |=∞

となるように定義されているとする．このとき

n^* := min{ k∈N | k≧n, f(k)＼∪_m<ng(m)≠ ∅, (X＼f(k))＼∪_m<ng(m)≠ ∅ }
A_n := f(n^*)∪∪_m<ng(m)

として

g(n) := f(n^*)＼∪_m<ng(m)　(|{ f(k)＼A_n | k > n^* }| =∞のとき)
g(n) := X＼(f(n^*)＼∪_m<ng(m))　(それ以外のとき)

と定める．

このとき h: X→N を

h(x) := n　(あるnに対してx∈g(n) となるとき)
h(x) := 0　(それ以外のとき)

と定めれば h は全射である．

命題22 次の命題は( ZF 上)同値である．

1. 任意のDedekind有限集合は有限集合である(即ち P(IV, I) )．
2. 任意のDedekind有限集合はamorphousである．
3. 任意のDedekind有限集合はII-finiteである(即ち P(IV, II) )．
4. Dedekind有限集合の冪集合はDedekind有限集合である(即ち P(IV, III) )．
5. Dedekind有限集合 X とDedekind無限集合 Y に対し |X|≦|Y| ．
6. 非可算集合 X と可算集合 Y に対し |X∪Y|=|X| ．
7. 非可算集合 X と可算集合 Y に対し |X＼Y|=|X| ．
8. |X| > ₀ かつ |Y|=₀ ならば |X＼Y| > ₀ ．
9. 任意の集合 X に対し ₀≦|X| または |X|≦₀ ．

証明 1⇒2，2⇒3，3⇒4は明らか．

(4 ⇒ 1) Dedekind有限な無限集合 X が存在すると仮定する． X が無限集合だから P(X)∋Y |→ |Y|∈N は全射である．即ち ₀≦^*|P(X)| となる．従って補題21により P(P(X)) はDedekind無限集合である．一方 X がDedekind有限だから仮定5により P(P(X)) がDedekind有限集合となり矛盾する．

(1 ⇒ 5) 仮定1よりDedekind有限集合は有限集合だから明らか．

(5 ⇒ 1) X をDedekind有限集合とする． N はDedekind無限集合だから仮定6により |X|≦₀ ．よって X が無限集合と仮定すると X は可算無限，即ちDedekind無限集合となって矛盾する．

(1 ⇒ 6) X を非可算集合， Y を可算集合とする．仮定より X はDedekind無限集合である． |Y＼X|≦₀ だから命題4の条件6と7により

|X∪Y|=|X|+|Y＼X|=|X|.

(6 ⇒ 7) X を非可算集合， Y を可算集合とすると X＼Y も非可算集合である．故に仮定7により |X|=|(X＼Y)∪Y|=|X＼Y| ．

(7 ⇒ 8)明らか．

(8 ⇒ 1) X を無限集合とする． X が可算無限ならば明らかにDedekind無限だから， X は非可算無限集合としてよい．このとき |XN| > ₀ だから仮定9により |X|=|(XN)＼N| > ₀ となり， X はDedekind無限集合である．

(1 ⇔ 9)明らか．