このページでは「圏」と書いたら特に断らない限り「小さい圏」を表すものとする．

を互いに素な非空集合の族とする．圏 X, Λ を次のように定める．

• まず Λ は離散圏とする．即ち Ob(Λ) := Λ で

  |Hom_Λ(λ, ν)| = 1　(λ=νのとき)
  |Hom_Λ(λ, ν)| = 0　(λ≠νのとき)

• X については Ob(X) := ∪_λ∈ΛX_λ として

  |Hom_X(x, y)| = 1　(あるλ∈Λについてx, y∈X_λとなるとき)
  |Hom_X(x, y)| = 0　(それ以外)

関手 L: X→Λ を Lx := 「 x∈X_λ となる λ∈Λ 」で定める．このように定義すれば， の選択関数とは L の右随伴関手のことである．

故に，随伴関手の存在に関する定理から選択公理を導くことができる．

定理 次の命題は( ZF 上)同値．

1. 選択公理
2. C, D を圏， F: C→D を関手とする．任意の d∈D に対して F から d への普遍射が存在するならば， F は右随伴を持つ．
3. C を余完備な圏， D を圏， F: C→D を余連続な関手とする． F はsolution set conditionを満たすとする．このとき F は右随伴を持つ．(General Adjoint Functor Theorem)
4. C を余完備かつco-wellpoweredで，generatoring setを持つ圏， D を圏， F: C→D を余連続な関手とする．このとき F は右随伴を持つ．(Special Adjoint Functor Theorem)
5. C, D, U を圏， F: C→D ， E: C→U を関手として，各 d∈D に対して余極限 colim(F↓d→C→U) が存在するとする．このとき F に沿った E の左Kan拡張 F^†E が存在し， F^†E(d) ≅ colim(F↓d→C→U) である．

証明 1⇒2，1⇒3，1⇒4，1⇒5 は省略する．

(2 ⇒ 1) を互いに素な非空集合の族とする． C, D, F として，上で定義した X, Λ, L を取る． λ∈Λ とすると，任意の x∈X_λ に対して一意な射 Lx→λ が普遍射である．よって L が右随伴を持つ．

(3 ⇒ 1) を互いに素な非空集合の族とする．どの X_λ にも含まれない元 0, 1 を取っておく． 0, 1 ∉ Λ としてよい．圏 C, D を次のように定める．

• Ob(C) := 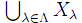∪ { 0, 1 }
• |Hom_C(x, y)| = 1　(あるλ∈Λについてx, y∈X_λとなるとき)
  |Hom_C(x, y)| = 1　(x=0 または y=1 のとき)
  |Hom_C(x, y)| = 0　(それ以外)
• Ob(D) := Λ∪{ 0, 1 }
• |Hom_D(x, y)| = 1　(x=0 または y=1 または x=y のとき)
  |Hom_D(x, y)| = 0　(それ以外)

関手 F: C→D を

Fx := 0　(x=0 のとき)
Fx := 1　(x=1 のとき)
Fx := λ　(x∈X_λのとき)

で定める．このとき C は余完備， F は余連続でsolution set conditionを満たす．故に右随伴 G: D→C が存在する．すると x∈X_μ ， λ∈Λ に対して Hom_D(Fx, λ) ≅ Hom_C(x, Gλ) だから， Gλ∈X_λ となり， G は選択関数である．

(4 ⇒ 1)3 ⇒ 1と同じ圏を使用すればよい．

(5 ⇒ 1) を互いに素な非空集合の族とする． C, D, F として，上で定義した X, Λ, L を取る．また U := X ， E := id_X と定める．

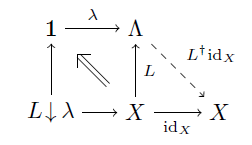
任意の λ∈Λ に対して余極限 colim(L↓λ→X→id_X) は明らかに存在する．よって L^†id_X: Λ→X が存在する． λ∈Λ を取る． X_λ≠ ∅ だから， x∈X_λ が取れる．このとき Lx=λ である．自然変換 η: id_X⇒(L^†id_X)L から射 η_x: x→L^†id_X(Lx) = L^†id_X(λ) が得られる．よって圏 X の定義から L^†id_X(λ)∈X_λ でなければならない．

X^op = X ， Λ^op = Λ であるから，選択関数は L: X→Λ の左随伴関手であることも分かる．よって，先の命題の双対も選択公理と同値である．(省略)

定義 圏 C が骨格的 ⇔ f: c→d が同型射ならば c=d ．

定義 圏 C の骨格的な充満部分圏 S⊂C で「任意の c∈C に対してある s∈S が存在して c ≅ s となる」を満たすものを C の骨格という．

定理 次の命題は( ZF 上)同値．

1. 選択公理
2. 任意の圏は骨格を持つ．
3. 圏の骨格は(もし存在するならば)同型を除いて一意である．

証明 (1 ⇒ 2) C を圏とする．選択公理により，商集合 Ob(C)/≅ の完全代表系 S を取る． S を充満部分圏 S⊂C と見なせば， S が骨格である．

(2 ⇒ 1) を互いに素な非空集合の族とする．上で定義した圏 X の骨格 S を取れば，明らかに Ob(S) が の選択集合である．

(1 ⇒ 3) C を圏， S, T⊂C を骨格とする． s∈S とすると， T が骨格だから Fs∈T が一意に存在して s ≅ Fs となる．このとき A_s := { f: s→Fs | f は同型射 } ≠ ∅ である．よって選択公理により (f_s)_s∈S∈Π_s∈SA_s を取ることができる． f: s₀→s₁ に対して Ff: Fs₀→Fs₁ を Ff := f_s1ff_s0^-1 により定めれば， F: S→T は関手である．

この F が圏同型である．

(3 ⇒ 1) 選択公理と同値な次の命題を示す．

非空集合の族 { X_λ } _λ∈Λ は全ての X_λ の濃度が等しいとする．このときある λ₀∈Λと写像の族 { f_λ } _λ∈Λ が存在して「各 λ∈Λに対して f_λ: Aut(X_λ0)→Aut(X_λ) は群同型」を満たす．

を非空集合の族で， λ≠μ に対して |X_λ| = |X_μ| であるとする． λ₀∈Λ を一つ取る．圏 C を Ob(C) := Λ×{ 0, 1 } で

Hom_C(<λ, i>, <μ, j>) = Bij(X_λ0, X_λ0)　(i=j=0, λ=μ)
Hom_C(<λ, i>, <μ, j>) = Bij(X_λ, X_λ)　(i=j=1, λ=μ)
Hom_C(<λ, i>, <μ, j>) = Bij(X_λ0, X_λ)　(i=0, j=1, λ=μ)
Hom_C(<λ, i>, <μ, j>) = Bij(X_λ, X_λ0)　(i=1, j=0, λ=μ)
Hom_C(<λ, i>, <μ, j>) = ∅　(それ以外).

但し，Bij(X, Y) := { f: X→Y | fは全単射 }

により定める． i=0, 1 に対して C_i := Λ×{ i } と置けば，明らかに C₀, C₁⊂C は骨格である．故に仮定3により圏同型 F: C₀→C₁ が存在する．関手 F から全単射 F_λ: Aut(X_λ0)→Aut(X_λ) が得られる．

定義 C を圏， i, p∈Mor(C) を射とする．i が p に対してleft lifting propertyを持つ，もしくは p が i に対してright lifting propertyを持つとは，任意の可換図式

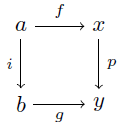
に対して射 h: b→x が存在して，次の図式が可換となることである．

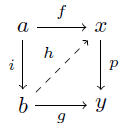
定義 C を(小さいとは限らない)圏，L, R⊂Mor(C) を部分クラスとする．(L, R) が C のweak factorization systemであるとは，以下の条件を満たすことを言う．

1. 任意の射 f∈Mor(C) に対して，ある i∈L ， p∈R が存在して f=pi と書ける．
2. i∈L ⇔ i は任意の p∈R に対してleft lifting propertyを持つ．
3. p∈R ⇔ p は任意の i∈L に対してright lifting propertyを持つ．

命題1 (L, R₀), (L, R₁) が圏 C のweak factorization systemならば R₀=R₁

証明 p∈R₀ とする． (L, R₀) がweak factorization systemだから，任意の i∈L に対してright lifting propertyを持つ．よって， (L, R₁) がweak factorization systemだから， p∈R₁ となる．即ち R₀⊂R₁ である．同様にして R₁⊂R₀ だから R₀=R₁ となる．

定義 Mono, Epi, SplitEpi⊂Mor(Set) を以下のように定義する．

Mono := { f∈Mor(Set) | f は単射 }
Epi := { f∈Mor(Set) | f は全射 }
SplitEpi := { f∈Mor(Set) | f は全射で，ある写像 g が存在して fg=idとなる }

命題 (Epi, Mono) は Set のweak factorization systemである．

証明 省略

命題2 (Mono, SplitEpi) は Set のweak factorization systemである．

証明 任意の写像 f が f=em ， m∈Mono ， e∈SplitEpi と分解できることは容易に分かる．

m∈Mono，e∈SplitEpi として任意の可換図式

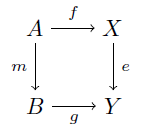
を考える． m: A→B は単射だから A⊂B としてよい．また e∈SplitEpi だから，ある写像 s: Y→X が存在して es=id_Y となる．写像 h: B→X を， b∈B に対して

h(b) := f(b)　(b∈Aのとき)
h(b) := s(g(b))　(b∈B＼Aのとき)

と定める．このとき明らかに hm=f である．また b∈A のとき

eh(b) = e(h(b)) = e(f(b)) = g(b)

であり， b∈B＼A のとき

eh(b) = e(h(b)) = e(s(g(b))) = g(b)

となるから eh=g である．以上により m∈Mono が e∈SplitEpi に対してleft lifting propertyを持つ(即ち e∈SplitEpi が e∈Mono に対してright lifting propertyを持つ)ことが分かる．

写像 f: X→Y が任意の e∈SplitEpi に対してleft lifting propertyを持つとする．次の実線は可換である．

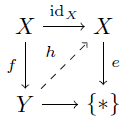
明らかに e∈SplitEpi だから，写像 h: Y→X が存在して可換となる．即ち id_X=hf だから f は単射である．

写像 f: X→Y が任意の m∈Mono に対してright lifting propertyを持つとする．次の実線は可換である．

m∈Mono だから，写像 h: Y→X が存在して可換となる．即ち id_Y=fh だから f∈SplitEpi である．

定理 選択公理 ⇔ (Mono, Epi) は Set のweak factorization systemである．

証明 「任意の全射 F: X→Y に対して，ある G: Y→X が存在して FG=id_Y 」が選択公理と同値であった．故に命題1と命題2から明らか．

定義 C, D を圏とする． C から D へのanafunctorとは組 F = <|F|, F^, F> であって以下を満たすものを言う．

1. |F| は圏である．
2. F^: |F|→C ， F: |F|→D は関手である．
3. F^ は忠実充満で，対象について全射である．

記号で F: C →^a D と表す．

定義 F, G: C→^a D をanafunctorとする． F から G への自然変換とは，次の図式の自然変換 φ のことをいう．( |F|×_C|G| は F^ と G^ のpullbackである．)

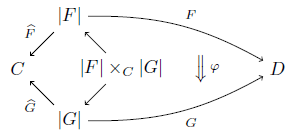
F: C→D を関手とするとき， id: C→C と F: C→D により F をanafunctor F: C→^a D とみなすことができる．

定理 次の命題は( ZF 上)同値．

1. 選択公理
2. 関手 F: C→D が圏同値 ⇔ F が忠実充満かつ本質的全射
3. 任意のanafunctor F: C→^a D に対して，ある関手 G: C→D が存在して F ≅ G となる．

証明 (1 ⇒ 2) 省略．

(2 ⇒ 3) F: C→^a D をanafunctorとする． F^ は忠実充満かつ本質的全射だから，仮定2より関手 K: C→|F| で F^K ≅ id_C，KF^ ≅ id_|F| となるものが存在する．G := FK とする．

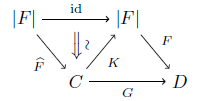
このとき F ≅ GF^ だから，anafunctorとして F ≅ G である．

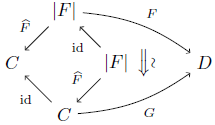
(3 ⇒ 1) を互いに素な非空集合として，最初に述べたように圏 X, Λ と関手 L: X→Λ を取る． 組<X, L, id_X> はanafunctor F: Λ→^a X を定めるから，ある関手 G: Λ→X が存在して F ≅ G となる．即ち自然同型 φ: id⇒GL が存在する．

λ∈Λ に対して x∈X_λ を取れば G(λ)=G(L(x))=id(x)=x∈X_λ となるから G は選択関数である．

定理 選択公理
⇔ C を圏，x∈C を対象とする．任意の a∈C に対して直積 a×x が存在するならば，関手 F: C→C で「任意の a∈C に対して Fa ≅ a×x 」となるものが存在する．

証明 ( ⇒ ) 省略．

( ⇐ ) を互いに素な非空集合の族とする． Λ∩= ∅ としてよい． ∞ ∉ Λ∪ となる元 ∞ を一つ取り，圏 C を以下のように定める．

• Ob(C) := { ∞ }∪Λ∪．

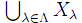• a, b∈C に対して以下のように定める．

  Hom_C(a, b) := 1　(a=bのとき)
  Hom_C(a, b) := 1　(b∈Λ, a∈X_bのとき)
  Hom_C(a, b) := 1　(b=∞, a∈X_λのとき)
  Hom_C(a, b) := 1　(ある λ∈Λ に対して a, b∈X_λ のとき)
  Hom_C(a, b) := 0　(それ以外のとき)
  

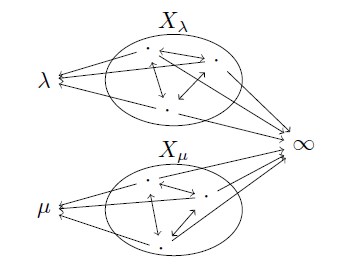
このとき明らかに，任意の a∈C に対して直積 a×∞ が存在する．(特に λ∈Λ に対して λ×∞∈X_λ である．) よって仮定により関手 F: C→C で，任意の a∈C に対して Fa ≅ a×∞ となるものが存在する．このとき F(λ)∈X_λ となるから F|_Λ: Λ→ が選択関数である．