定義 Rを集合X上の二項関係とする．

1. Rが反射的 ⇔ 任意のx∈Xに対してxRx
2. Rが反対称的 ⇔ xRyかつyRxならばx=y
3. Rが推移的 ⇔ xRyかつyRzならばxRz
4. Rがconnected ⇔ xRyまたはx=yまたはyRx
5. Rが前順序関係 ⇔ Rが反射的かつ推移的
6. Rが順序関係 ⇔ Rが反対称的な前順序関係
7. Rが全順序関係 ⇔ Rがconnectedな順序関係
8. x∈Xが極大元 ⇔ 全てのy∈Xに対し「xRyならばyRx」
9. x∈Xが最小元 ⇔ 全てのy∈Xに対し「x≠yならばxRy」
10. x∈XがY⊂Xの上界 ⇔ 全てのy∈Yに対し「x≠yならばyRx」
11. Rが整列順序関係 ⇔ Rが順序関係で，任意のY(≠∅)⊂Xに対して(Y, R)が最小元を持つ．
12. Xが有限性を持つ ⇔「x∈X⇔ xの任意の有限部分集合yに対しy∈X」
13. x∈Xに対してx^↓ := { y∈X | yRx }
14. Y⊂Xが鎖 ⇔ (Y, R)が全順序集合

定義 (X, ≦)を順序集合とする．

1. Y⊂Xが反鎖 ⇔ 任意のx, y∈Yに対して「x≠yならば￢x≦y, ￢y≦x」
2. (X, ≦)がramified ⇔ 任意の元x∈Xに対し(x^↓, ≦)が鎖になる

定義 Xを集合，R⊂X×Xを二項関係とする．

1. R^-1 := { <a, b>∈X×X | <b, a>∈R }
2. R^c := { <a, b>∈X×X | <a, b>∉ R }
3. I := {< a, a>∈X×X | a∈X }

定理1 次の命題は(ZF上)同値．

1. 順序集合Xが「Xの鎖には上界が存在する」を満たすならば，Xの極大元が存在する．(Zornの補題)
2. 集合X上の推移的関係Rに対して極大鎖Y⊂Xが存在する．
3. 順序集合(X, ⊂)は極大鎖を持つ．
4. 順序集合(X, ⊂)が「任意の鎖C⊂Xに対してあるx∈Xが存在して， 任意のy∈Cに対してy⊂x」を満たすならば，Xの極大元が存在する．
5. 順序集合(X, ⊂)が「任意の鎖C⊂Xに対して∪_{y∈C}y∈X」を満たすならば，Xは極大元を持つ．
6. 有限性をもつ非空集合Xは(⊂に関する)極大元をもつ．(Tukeyの補題)
7. 任意の前順序集合(X, ≦)は極大鎖を持つ．
8. 任意の順序集合(X, ≦)は極大鎖を持つ．(Hausdorff's Maximal chain Condition)
9. 任意の順序集合(X, ≦)の任意の鎖は，Xのある極大鎖に含まれる．
10. 任意の前順序集合(X, ≦)は極大反鎖を持つ．
11. 任意の順序集合(X, ≦)は極大反鎖を持つ．(Kurepa's Maximal Antichain Condition)

証明 (1 ⇒ 2) C := { Y⊂X | (Y, R)は鎖 } と定め，⊂でCに順序を入れる．この(C, ⊂)はZornの補題の仮定を満たす．

よってZornの補題より極大元Y∈Cが存在するが，これが極大鎖である．

(2 ⇒ 3) ⊂は推移的だから，仮定2より⊂によって全順序付けされる極大部分集合が存在するが，これは明らかに(X, ⊂)の極大鎖である．

(3 ⇒ 4) 仮定3より極大鎖Y⊂Xが存在する． このYに4の仮定を適用すると，あるx∈Xが存在して， 任意のy∈Yに対してy⊂xとできる．このxがXの極大元である．

(4 ⇒ 5) 明らか

(5 ⇒ 6) Xが有限性を持つとする．順序集合(X, ⊂)が5の仮定を満たすことを示せばよい． C⊂Xを鎖としてx := ∪_y∈C y と置く．z⊂xを任意の有限部分集合とする．xの定義とzが有限集合であることから z⊂y₁∪ y₂∪…∪y_n となるy_i∈Cが存在する．(C, ⊂)が全順序であるからy := max{ y₁, y₂, …, y_n } が存在してz⊂yとなることが分かる．y∈C⊂X，即ちy∈XだからXが有限性を持つ事よりz∈Xである．

従って再びXが有限性を持つ事からx∈Xである．

(6 ⇒ 7) C := { Y⊂X | Yは鎖 } は空ではない．明らかにCは有限性を持つので，Tukeyの補題より極大元を持つ．

(7 ⇒ 8)は明らか．

(8 ⇒ 9) C⊂Xを鎖とする．集合 Y := { y∈X | 任意のx∈Cに対してx≦yまたはy≦x } を考える．明らかにC⊂Yである．(Y, ≦)は順序集合だから，仮定7より極大鎖D⊂Yを持つ．C⊂Dである．

￢C⊂Dと仮定する．x∈C＼Dが取れる．Dの極大性よりD∪{x}⊂Yは鎖ではない．故にあるy∈D⊂Yが存在して￢x≦yかつ￢y≦xとなるが，それはYの定義に矛盾する．

鎖E⊂XがD⊂Eを満たすとする． するとC⊂D⊂EだからYの定義によりE⊂Yである． 即ちEはYの鎖でもある．故にDの極大性によりE=Dである．即ちDはCを含むXの極大鎖である．

(9 ⇒ 8)明らか．

(8 ⇒ 1) Zornの補題と同値な整列可能定理を示す．その為にXを任意の集合とし A := { f: α→A | αは順序数でfは単射 } と置く．(A, ⊂)は順序集合である．よって極大鎖Cを持つ．するとg := ∪_f∈C f はある順序数からXへの単射である．Cの極大性からgは全射．故にXは整列可能である．

(6 ⇒ 10) C := { Y⊂X | Yは反鎖 } は空でない．明らかにCは有限性を持つので，Tukeyの補題より極大元を持つ．

(10 ⇒ 11) 明らか．

11 ⇒ 1) Zornの補題と同値な整列可能定理を示す．その為に，整列可能定理と同値な「全順序集合は整列可能」を示す．

整列可能定理についての定理4を参照．

(X, ≦)を全順序集合とする．A := { (Y, y) | Y⊂X, y∈Y } と置き，Aの順序を

(Y, y)≦(Z, z) ⇔ Y=Zかつy≦z

で定める．(y≦zはXの順序である．) 仮定10より極大反鎖C⊂Aが存在する．Xは全順序だから，明らかC = { (Y, f(Y)) | Y∈P(X)＼{∅} } と書ける．このfは P(X)＼{∅} の選択関数である．よって選択公理から整列可能定理を導くのと同様にしてXが整列可能なことが分かる．

整列可能定理とZornの補題を参照．

定義 Xを集合とする．便宜上，次のように定める．

1. (X, R)が関係 ⇔ RはX上の二項関係
2. (X, R)が推移 ⇔ RはX上の推移的関係
3. (X, R)が反対称 ⇔ RはX上の反対称的関係
4. (X, R)が連結 ⇔ RはX上のconnectedな関係
5. (X, R)が順序 ⇔ (X, R)は順序集合
6. (X, R)が全 ⇔ (X, R)は全順序集合
7. (X, R)が整列 ⇔(X, R)は整列順序集合
8. (X, R)が有向 ⇔ (X, R)は有向順序集合
9. (X, R)が分岐 ⇔ (X, R)はramifiedな順序集合
10. (X, R)が森 ⇔ (X, R)は順序で，任意のx∈Xに対し(x^↓, R)が整列順序集合
11. (X, R)が木 ⇔ (X, R)が森で，最小元を持つ
12. (X, R)が推連 ⇔ (X, R)は推移かつ連結である
13. (X, R)が反連 ⇔ (X, R)は反対称かつ連結である

以上のように定めたとき，MP(P, Q)で命題

Xは任意の集合で，(X, R)はPであるとする．もし「任意のY⊂Xに対して「(Y, R)がQになるならばYはXに上界を持つ」」が成り立つならば，Xは極大元を持つ．

を表す．例えばMP(順序, 全)はZornの補題である．

定理2 Zornの補題 ⇔ MP(推移, 整列)

証明 ←は明らか．逆⇒を示す．その為に，Zornの補題と同値な定理1の2を用いる．

RをX上の推移的関係とし，任意の部分整列順序は上界を持つとする．部分集合Y⊂Xに対して Y^⇓ := ∪_y∈Y y^↓ = { z∈X | あるy∈Yが存在してzRy } と書くことにする．W := { Y⊂X | (Y, R)は整列順序集合 } と置く．W上の関係≦を

Y≦Z ⇔ Y⊂Z かつ Z∩Y^⇓⊂Y

と定める．≦はWの推移的関係である．

故に定理1の2により極大鎖V⊂(W, ≦)が存在する．Z := ∪_Y∈V Y とする．明らかに(Z, R)は順序集合である．任意のA(≠∅ )⊂Zを取る．Zの定義からあるY∈Vが存在してY∩A≠ ∅ である．Y∈V⊂Wだから，(Y, R)は整列順序．よってx := min(Y∩A) が存在する．このxはAの最小元でもある．

よって(Z, R)は整列順序集合である事が分かる．故にZ∈Wである．このZは(W, ≦)の極大元である．

A∈WがZ≦Aを満たすとする．Zの定義から，任意のYVに対しY≦Z，よってY≦Aである．即ちV∪{A}は(W, ≦)の鎖である．Vの極大性から V = V∪{A} となる，従ってA∈V，よってA≦Zとなる．即ちZは極大元である．

(Z, R)⊂Xは整列順序だったから，MP(推移, 整列)の仮定によりZの上界x∈Xが存在する．

y∈XがxRyを満たすとする．勿論yはZの上界である．yRzとなるz∈Zが存在する．

「全てのz∈Zに対し￢yRz」と仮定する．(Z∪{y}, R)は整列順序だから，Z∈Wの極大性から Z = Z∪{y} である．従ってy∈Z，故に￢yRyである．一方xがZの上界であることからyRxであり，ゆえにxRyからyRyとなり矛盾する．

このとき推移律からxRzである．するとxがZの上界であることからz=xまたはzRxであるが，どちらにしてもyRxである．従ってxが(X, R)の極大元であることが分かった．

定理3 P, Qが次のいずれかであるとき，MP(P, Q)はZornの補題と同値である．

P = 推移, 順序, 分岐, 森
Q = 連結, 反連, 推連, 全, 有向, 整列

証明 まず，定理2で示したようにZornの補題 ⇔ MP(推移, 整列)である．次に，MP(森, 有向) ⇒ MP(森, 連結)である．

(X, ≦)を森とし，Xの任意の部分連結集合が上界を持つとする．Y⊂Xを部分有向集合とする．x, y∈Yとすると，Yは有向集合だからあるz∈Yが存在してx≦z, y≦zである．よってx, y∈z^↓⊂Xであり，今Xは森だからz^↓は整列順序集合．故にx≦yまたはy≦xである．即ち，Yは連結である．従って上界を持つ．故に仮定のMP(森, 有向)からXは極大元を持つ．

P⇒P', Q⇒Q'であればMP(P', Q)⇒MP(P, Q)，MP(P, Q)⇒MP(P, Q') である．またP⇒QであることをP→Qと書いて図示すると次のようになる．

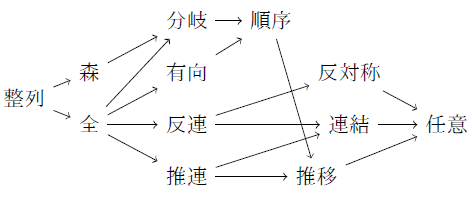
以上により次の図式が分かる．

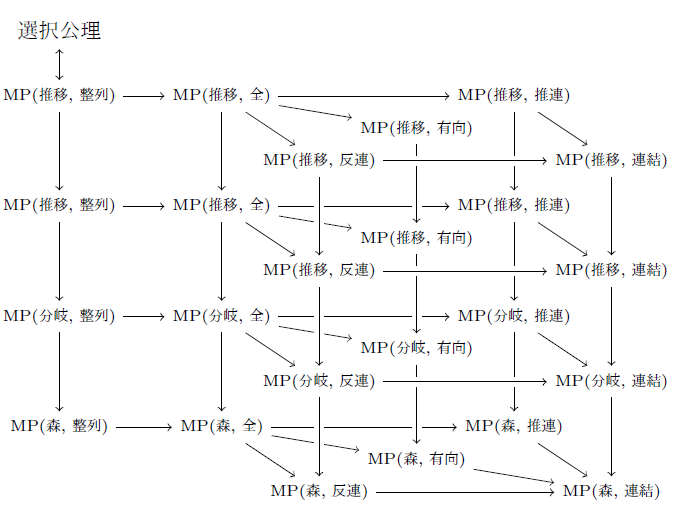
よって後は MP(森, 連結)⇒MP(推移, 整列) を示せばよい．

(X, R)を推移とし，Xの任意の部分整列順序が上界を持つとする．W := { Y⊂X | (R, ≦)は整列順序 } と置く．Wの二項関係≦を

Y≦Z ⇔ Y=Zまたはあるz∈Zが存在してY=z^↓

と定める．すると(W, ≦)は森である．連結部分集合V⊂Wを取ると，明らかに ∪_Y∈V Y がVの上界である．故にMP(森, 連結)によりWは極大元Y∈Wを持つ．Y⊂Xは部分整列順序だから，上界x∈Xを持つ．このxがXの極大元である．故にMP(推移, 整列)が示された．

定理4 Zornの補題⇔ MP(有向, 整列)

証明(⇒) MP(推移, 整列) ⇒ MP(有向, 整列)であるから明らか．

(←) MP(有向, 整列) ⇒ MP(森, 整列)を示せばよい．

(X, ≦)を森として，Xの部分整列順序は上界を持つとする．

Xは整列可能でないと仮定する．W := { (Y, R) | Y⊂X, (Y, R)は整列順序 } と置く． Wの順序≦を

(Y, R)≦(Z, S) ⇔ Y⊊Z または (Y=ZかつR=S)

で定める．(W, ≦)は有向集合である．

V⊂(W, ≦)を部分整列順序とする．Z := ∪_{(Y, R)∈V} Y と置く．z∈Zに対して(Y_z, R_z) := ≦-min{ (Y, R)∈V | z∈Y } とする．Zの順序Sを

zSw ⇔ (Y_z, R_z)<(Y_w, _w)または((Y_z, R_z)=(Y_w, _w)かつzR_zw)

で定めると，(Z, S)は整列順序である．故に(Z, S)∈WはVの上界である．故に仮定のMP(有向, 整列)により(W, ≦)は極大元(Y, R)を持つ．このとき明らかにY=Xであり，Xが整列可能でないことに矛盾する．

従ってXは整列可能である．(X, R)を整列順序とする．￢|λ|≦|X|を満たす順序数λを取る．Xに含まれない元 ∞ ∉ X を一つ取っておく．f: λ→X∪{∞}を

f(α) := R-min{ x∈X＼{f(β)|β<α} | 任意のβ<αに対してf(β)≦x }

で定める(ただし，このようなminが存在しないときはf(α):=∞とする)．fの定義から，f(α)=f(β)≠∞ならばα=βである．λの取り方からfは単射でないので，f(α)=∞となるα<λは存在する．そこでγ := min{ α<λ | f(α)=∞ } と置く．Y := { f(β) | β<γ } とすればY⊂(X, ≦)は部分整列順序である．故に上界x∈Xを持つ．このときxが極大元である．

定理5 次の命題は(ZF上)同値．

1. Zornの補題
2. 順序集合Xが「Xの部分整列順序は上界を持つ」を満たすならば，Xの極大元が存在する．
3. 順序集合Xが「Xの部分整列順序は上限を持つ」を満たすならば，Xの極大元が存在する．
4. 順序集合Xが「Xの鎖は上限を持つ」を満たすならば，Xの極大元が存在する．
5. 順序集合(X, ⊂)が「任意の部分整列順序Y⊂Xに対して∪_{y∈Y}y∈X」を満たすならば，Xは極大元を持つ．

証明 2 はMP(順序, 整列)だから，定理3により 1⇔2 である．また 2⇒3，3⇒4，3⇒5 は明らか．

4⇒1 と 5⇒1 は定理1の条件5が成り立つことから分かる．

MS(P, Q)で命題

(X, R)がPのとき，集合{ Y⊂X | (Y, R)はQである } は⊂に関する極大元を持つ

を表すとする．

定理6 次の(P, Q)に対して Zornの補題 ⇔ MS(P, Q) である．

• P=関係，推移，Q=反対称，連結，反連，推連，順序，全，有向，分岐
• P=反対称，Q=連結，反連，推連，全，有向，分岐
• P=連結，Q=反対称，連結，順序，全，有向，分岐
• P=順序，Q=連結，反連，推連，全，有向，分岐
• P=有向，Q=連結，反連，推連，全，分岐
• P=分岐，Q=連結，反連，推連，全，有向
• P=森，Q=連結，反連，推連，全，有向，整列

証明 (1) P⇒P' ならば MP(P', Q)⇒MP(P, Q) である．

(2) 関係R⊂X×Xに対して「(X, R)が連結 ⇔ (X, R^c)が反対称」「(X, R∪I)が全 ⇔ (X, R^c∪I)が全」が成り立つ．故に MP(反対称, 連結)⇔MP(連結, 反対称) と MP(反対称, 反連)⇔MP(連結, 反連) と MP(反対称, 全)⇔MP(連結, 全) と MP(関係, 反対称)⇔MP(関係, 連結) が分かる．

(3) 次の同値は明らかである．

• MP(推移, 反対称) ⇔ MP(推移, 順序)
• MP(連結, 順序) ⇔ MP(連結, 全) ⇔ MP(連結, 有向) ⇔ MP(連結, 分岐)
• MP(有向, 連結) ⇔ MP(有向, 反連) ⇔ MP(有向, 推連) ⇔ MP(有向, 全) ⇔ MP(有向, 分岐)
• MP(森, 連結) ⇔ MP(森, 反連) ⇔ MP(森, 推連) ⇔ MP(森, 全) ⇔ MP(森, 有向) ⇔ MP(森, 整列)

以上の(1)(2)(3)を合わせると，次の図式が得られる． (ここで黒矢印は(1)，青い太線の矢印は(2)，赤い点線の矢印は(3)による．また MS(P, Q) を P/Q で表した．四角い枠については後述．)



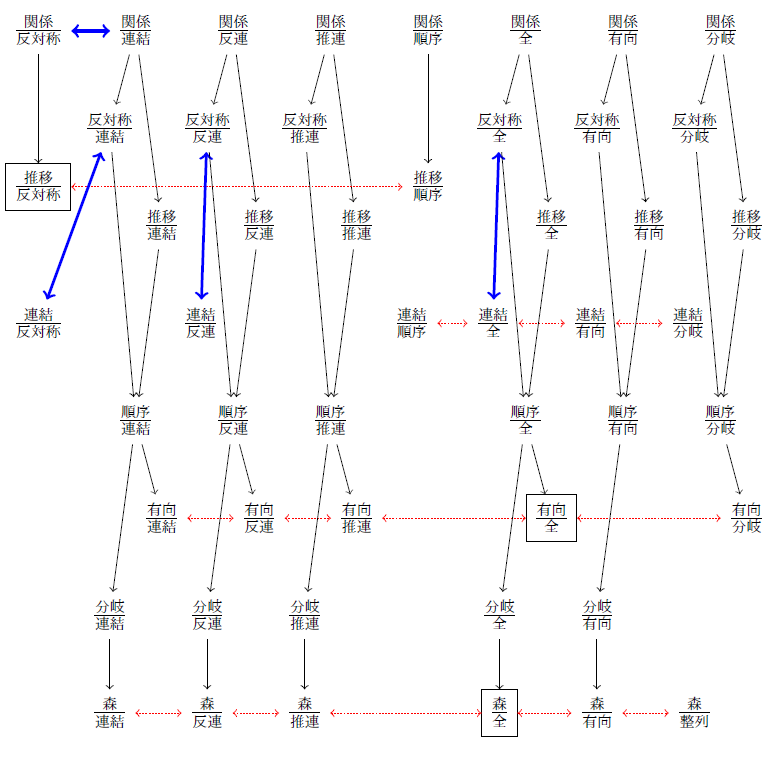
また，Q= 反対称，連結，反連，推連，順序，全，有向，分岐のとき，Zornの補題⇒MP(関係, Q) である．よって後は「図中で四角に囲まれた命題 ⇒ Zornの補題」，即ち次の(i)(i)(iii)を示せばよい．

(i) MS(有向, 全) ⇒ Zornの補題
定理1の条件7「任意の順序集合は極大鎖を持つ」を示す．(X, ≦)を順序集合とする．C := { Y⊂X | (Y, ≦)は鎖 } とすると(C, ⊃)は有向集合になる．よって仮定のMS(有向, 全)により極大な部分全順序M⊂Cが存在する．このとき Z := ∪_Y∈M Y と置けば明らかにこのZ⊂Xが極大鎖である．

(ii) MS(森, 全) ⇒ Zornの補題
MP(順序, 整列)を示す．(X, ≦)を順序集合として，Xの部分整列順序は上界を持つとする．W := { Y⊂X | (Y, ≦)は整列順序 } として，Wに順序≦を

Y≦Z ⇔ Y=Z または あるz∈Zが存在してY=z^↓

で定める．すると(W, ≦)は森になる．よって仮定のMS(森, 全)により極大な部分全順序V⊂Wが存在する．このとき Z := ∪_Y∈V Y と置けば明らかにZ∈Wだから，Zの上界x∈Xが存在する．このxが極大元である．

(iii) MS(推移, 反対称) ⇒ Zornの補題
選択集合の存在を示す．その為にを互いに素な非空集合の族とする．に関係Rを

xRy ⇔ あるλ∈Λ が存在してx, y∈X_λ

と定める．Rは勿論推移的であるから，仮定のMS(推移, 反対称)により極大なYを得る．このYがの選択集合である．

MS'(P, Q)で命題

(X, R)がPであり，Y⊂X で(Y, R)がQであるとする．このとき集合 { Z⊂X | Y⊂Z，(Z, R)はQである } は⊂に関する極大元を持つ

を表すとする．

定理7 定理6で述べた組(P, Q)のうち，(森, 整列)を除いて Zornの補題⇔MS'(P, Q) である．

証明 定理6と同様にして Zornの補題⇒MS'(P, Q) が分かる．一方，明らかに MS'(P, Q)⇒MS(P, Q) であるから MS'(P, Q)⇒Zornの補題 である．

定理8 Zornの補題
⇔ 順序集合Xが「下の条件(*)を満たす任意のA⊂Xが上界を持つ」を満たすならば，Xは極大元を持つ．

(*)　任意の元x, y∈Aに対し{x, y}⊂AはAに上界を持つ．

証明(⇒) Xを順序集合とする．(*)を満たすA⊂Xが上界を持つとする．C⊂Xを任意の鎖とすると鎖は(*)を満たすから，Cは上界を持つ．従ってZornの補題よりXは極大元を持つ．

(←) 選択公理を示す．を非空集合の族とする．X := { f: Γ→ | Γ⊂Λ, f(λ)∈X_λ } と定める．Xに⊂で順序を入れる．

A⊂Xが(*)を満たすとする．g := ∪_f∈A f と置く．λ∈dom(g)を取る．dom(f₁), dom(f₂)∋λとなる任意のf₁, f₂∈Aを取る．条件(*)より，{f₁, f₂}はAに上界hを持つ．このとき h(λ) = f₁(λ) = f₂(λ) である．よってg(λ)は一意に定まる．故にgは写像であり，g∈Xとなる．明らかにgはAの上界である．

よって仮定よりXは極大元を持つが，それが選択関数である．

定理9 Zornの補題
⇔ 任意の集合Xは次の条件を満たす極大部分集合Y⊂Xを持つ．

任意の元a, b∈Y に対してa∈bまたはa=bまたはb∈a

証明(⇒) Tukeyの補題(定理1の5)により明らか．

(←) 整列可能定理を示す．Xを任意の集合として W := { (Y, R) | Y⊂X, R⊂Y×Y, (Y, R)は整列順序 } と定める．Wに順序関係<を次のように定義する．

(Y, R)<(Z, S) ⇔ あるz∈Zが存在して(Y, R)=(z^↓, S).

すると(W, ≦)は木である．W上の写像fを

f(Y, R) := { {R} }∪{ f(W, T) | (W, T)∈W, (W, T)<(Y, R) }

で定める．

(i) f(Y, R)=f(Z, S) ⇔ (Y, R)=(Z, S)

←は明らか． ⇒を示す．f(R)=f(S)かつ(Y, R)≠(Z, S)であるとする．するとR≠Sであるから{R}≠{S}となる．よって，f(R)⊂f(S)だから {R}∈{ f(W, T) | (W, T)∈W, (W, T)<(Z, S) } でなければならない．故にある(W, T)<(Z, S)が存在して R = f(W, T) となる．よって {T}∈f(W, T)=R⊂Y×Y となり矛盾する．

(ii) f(Y, R)∈f(Z, S) ⇔ (Y, R)<(Z, S)

←はfの定義から明らか． f(Y, R)∈f(Z, S)とする．するとfの定義よりf(Y, R)={S}かf(Y, R)∈{ f(W, T) | (W, T)∈W, (W, T)<(Z, S) } のどちらかである．しかしf(Y, R)={S}はありえない．故にある(W, T)<(Z, S)が存在してf(Y, R)=f(W, T)と書ける．すると(i)により(Y, R)=(W, T)となるから，(Y, R)<(Z, S)である．

集合f(W)に仮定を適用して，Q⊂f(W)を得る．V := f^-1(Q) と定める．(i)(ii)により，V⊂Wは「任意の(Y, R), (Z, S)∈Vに対し(Y, R)<(Z, S)または(Y, R)=(Z, S)または(Z, S)<(Y, R)」を満たす極大部分集合である．A := ∪_{(Y, R)∈V} Y, T := ∪_{(Y, R)∈V} R とすれば，明らかに(A, T)∈Wである．

X≠Aと仮定する．x∈X＼Aを取る．T' := T∪(A×{x})∪{ <x, x> } と置くと(A∪{x}, T')∈Wである．V' := V∪{ (A∪{x},T') } を考えると，これは「任意の(Y, R), (Z, S)∈V' に対し(Y, R)<(Z, S)または(Y, R)=(Z, S)または(Z, S)<(Y, R)」を満たす．明らかに V ⊊ V' だから V の極大性に矛盾する．よってX=Aであり，TはXを整列する．

定理10 集合Xと整数n≧2に対して，UN(X, n)で次の命題を表すとする．

任意のR⊂Xⁿに対して { Y⊂X | Yⁿ⊂R } は(⊂に関する)極大元をもつ．

n≧2を整数とするとき，次の命題は(ZF上)同値．

1. Zornの補題
2(n). 任意のXに対してUN(X, n)
3. あるn≧2が存在して任意のXに対しUN(X, n)
4. 任意のXに対してあるn≧2が存在してUN(X, n)

証明 1⇒2(n) と 2(n)⇒3 と 3⇒4 は明らか．

(4⇒2(2)) R⊂X×Xを二項関係とする．仮定4により，あるn≧2が存在してUN(X, n)が成り立つ．そこで R×X^n-2 にUN(X, n)を適用して極大なYを得る．このYは明らかに { Y⊂X | Y²⊂R } の極大元である．

(2(2)⇒1) 2(2)⇒MS(関係, 連結) を示せばよい．R⊂X×Xを二項関係とする．R∪R^-1∪I に2(2)を適用して { Y⊂X | Y²⊂R∪R^-1∪I } の極大元Yを得る．明らかに，このYが { Y⊂X | (Y, R)は連結 } の極大元である．

定義 集合Xに対し，二項関係を次のように定義する．

1. xDy ⇔ x∩y = ∅
2. xKy ⇔ x⊂y または y⊂x
3. xJy ⇔ ￢x⊂y かつ ￢y⊂x かつ x∩y≠∅

R⊂Xを関係とする．部分集合Y⊂Xが「任意の異なる二元x, y∈Yに対しxRy」を満たすとき， Yは property Rを持つということにする．

定理11 関係Rに対しN(R)で次の命題を表すとする．

任意のXに対し { Y⊂X | Yは property R を持つ } は極大元をもつ

このとき

Zornの補題⇔N(D)⇔N(D^c)⇔N(K)⇔N(J)⇔N(J^c)

証明 (Zornの補題⇒N(J)) Tukeyの補題より明らか．

(N(J) ⇒ N(D^c)) 任意の集合Xをとる．uを「任意のx, y∈Xに対し<x, u> ∉ y」を満たすように取り，x∈Xに対し f(x) := x∪{ <x, u> }と定める．仮定 N(J) を f(X) に適用すると，property Jを持つ極大部分集合S⊂f(X)の存在が分かる．Y := f^-1(S) と定める．

x, y∈X, x≠yとする．定義からf(x)K^cf(y)．故に f(x)Jf(y) ⇔ f(x)D^cf(y) が成り立つ．一方，f(x)∩f(y) = x∩y だから f(x)D^cf(y) ⇔ xD^cy となる．即ち f(x)Jf(y) ⇔ xD^cy であり，従って Y⊂X はproperty D^c を持ち極大である．

(N(D^c) ⇒ N(D)) 任意の集合Xをとる．x∈Xに対し f(x) := { {x} }∪{ {x, z} | z∈X, xDz } と置く．

x, y∈X, x≠yとする．定義から f(x)D^cf(y) ⇔ xDy である．よって仮定 N(D^c) を f(X) に適用すれば，N(D) の成立が分かる．

(N(D) ⇒ Zornの補題) 選択公理を示す．を互いに素な非空集合の族とする．X := { {<0, x>, <1, λ>} | λ∈Λ, x∈X_λ } とする．仮定 N(D)をXに適用して，property Dを持つ極大部分集合Y⊂Xを得る．{<0, x>, <1, λ>}D{<0, y>, <1, μ>} ⇔ λ≠μ だから，各λ∈Λに対し{<0, x_λ>, < 1, λ>}∈Yとなるようなx_λ∈X_λが唯一つ存在する．よって { x_λ | λ∈Λ } が選択集合である．

(Zornの補題⇒ N(J^c)) Tukeyの補題より明らか．

(N(J^c) ⇒ N(K)) 任意の集合Xをとる．∪_x∈X x に含まれない元uを取り，x∈Xに対しf(x) := x∪{u} と置く．すると任意のx, y∈X, x≠yに対しf(x)D^cf(y)となるから，f(x)J^cf(y)⇔ f(x)Kf(y)⇔ xKyが分かる．故に仮定N(J^c)をf(X)に適用すれば，N(K)の成立が分かる．

(N(K) ⇒ Zornの補題) 明らかにN(K)⇔「定理1の3」である．

定理12 Zornの補題⇔N(K^c)

証明 省略(PDF版参照)

定理13 Zornの補題
⇔ 順序集合(X, ≦)が「任意の鎖は上界を持つ」を満たすとき， あるt∈Xが存在して t^ := { x∈X | t<x } は最小元を持たない．

証明 省略(PDF版参照)