濃度の比較可能性
順序数や濃度の基本的な性質, Γ(X), K(X), κ*, κ† については順序数・濃度の簡単なまとめを参照.
定義 濃度 κ, λ が比較可能 ⇔ κ≦λ または λ≦κ
定理1 次の命題は( ZF 上)同値
- 選択公理
- 任意の濃度 κ, λ は比較可能
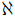 0≦κ, λ ならば κ, λ は比較可能
0≦κ, λ ならば κ, λ は比較可能- 任意の濃度 κ, λ について, κ≦*λ または λ≦*κ .
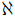 0≦κ, λ ならば κ≦*λ または λ≦*κ .
0≦κ, λ ならば κ≦*λ または λ≦*κ .
証明 (1 ⇒ 2) X と Y を任意の集合とする.整列可能定理により X, Y を整列する.すると整列順序の性質から | X |≦| Y | または | Y |≦| X | が分かる.
2 ⇒ 3と3 ⇒ 5と2 ⇒ 4と4 ⇒ 5は明らか.
(5 ⇒ 1)整列可能定理を示す. X を任意の集合として Y := X∪N とする.「 |A|≦*|B| ならば |A|≦|P(B)| 」であることに注意すると, |Γ(P(Y))|![]() |P(Y)| より |Γ(P(Y))|
|P(Y)| より |Γ(P(Y))|![]() *| Y | が分かる.従って仮定4から |Y|≦*|Γ(P(Y))| となる.よって全射 f: Γ(P(Y))→Y が存在する. Γ(P(Y)) は順序数だから, g(a) := min f-1(a) として単射 g: Y→Γ(P(Y)) が得られる.よって Y は整列可能であり, X⊂Y だから X も整列可能である.
*| Y | が分かる.従って仮定4から |Y|≦*|Γ(P(Y))| となる.よって全射 f: Γ(P(Y))→Y が存在する. Γ(P(Y)) は順序数だから, g(a) := min f-1(a) として単射 g: Y→Γ(P(Y)) が得られる.よって Y は整列可能であり, X⊂Y だから X も整列可能である.
濃度の比較可能性に制限を加えた,次の命題を考える.
命題2 任意の濃度 μ に対して「 μ≦κ0≦2μ, μ≦κ1≦2μ なる濃度 κ0, κ1 は比較可能」である.
補題3 命題2 ⇒ 無限順序数 α に対して |Γ(α)|≦|P(α)|
証明
α を無限順序数として κ := |P(α)| と置く. ![]() 0≦κ だから κ+1=κ である.また κ2=(2|α|)2=22|α|=2|α|=κ である.ここで κ† を考える. κ† の性質により κ < κ†≦2κ2 だから κ≦κ†≦2κ が分かる.一方 |Γ(α)|≦22|α|2=22|α|=2κ であるから κ≦κ+|Γ(α)|≦2κ+2κ=2κ+1=2κ となる.故に仮定から κ† と κ+|Γ(α)| は比較可能である.
0≦κ だから κ+1=κ である.また κ2=(2|α|)2=22|α|=2|α|=κ である.ここで κ† を考える. κ† の性質により κ < κ†≦2κ2 だから κ≦κ†≦2κ が分かる.一方 |Γ(α)|≦22|α|2=22|α|=2κ であるから κ≦κ+|Γ(α)|≦2κ+2κ=2κ+1=2κ となる.故に仮定から κ† と κ+|Γ(α)| は比較可能である.
(i) κ†≦κ+|Γ(α)| のとき
κ < κ†=2κ≦|Γ(α)| である.
順序数・濃度の簡単なまとめの命題16を参照.
κ=|P(α)| で, |Γ(α)| はアレフだから P(α) は整列可能である. |P(α)|![]() | α | だから Γ(α) の最小性により |Γ(α)|≦|P(α)| となる.
| α | だから Γ(α) の最小性により |Γ(α)|≦|P(α)| となる.
(ii) κ+|Γ(α)|≦κ† のとき
|Γ(α)|≦κ† である. κ†=|K(P(α))| だったから, W⊂K(P(α)) で |W| = |Γ(α)| となるものが取れる. K の定義より,各 f∈W はある順序数から P(α) への単射である. W は整列可能なので X := ∪f∈WIm(f) (⊂P(α)) も整列可能となる. ![]() =|X| と置く. X⊂P(α) だから Γ(X)≦Γ(P(α)) である.また X の定義より W⊂K(X) であり, | W |≦|K(X)| となる.ここで Γ(α)≦Γ(P(α)) であるが,もし Γ(α) < Γ(P(α)) ならば Γ(P(α)) の最小性より |Γ(α)|≦|P(α)| となるから, Γ(α)=Γ(P(α)) としてよい.このとき
=|X| と置く. X⊂P(α) だから Γ(X)≦Γ(P(α)) である.また X の定義より W⊂K(X) であり, | W |≦|K(X)| となる.ここで Γ(α)≦Γ(P(α)) であるが,もし Γ(α) < Γ(P(α)) ならば Γ(P(α)) の最小性より |Γ(α)|≦|P(α)| となるから, Γ(α)=Γ(P(α)) としてよい.このとき
![]() <
< ![]() *=|Γ(X)|≦|Γ(P(α))|=|Γ(α)|
*=|Γ(X)|≦|Γ(P(α))|=|Γ(α)|
となる.よって Γ(α) の最小性から ![]() ≦|α| なので
≦|α| なので
|Γ(α)|=|W|≦|K(X)|=![]() †=2
†=2![]() ≦2|α|=|P(α)|
≦2|α|=|P(α)|
である.
定理4 選択公理 ⇔ 命題2
証明 ⇒ は定理1より明らか. ⇐ を示す.その為には整列可能定理と同値な「順序数 α に対して P(α) は整列可能」を示せばよい.
整列可能定理についての定理4を参照.
α を順序数とする. α は無限順序数としてよい.順序数 Γ(α) に補題3を適用して | Γ(Γ(α)) |≦| P(Γ(α)) | を得る.よって | Γ(α) |≦| Γ(Γ(α)) |≦| P(Γ(α)) |=2| Γ(α) | となる. | α |≦| Γ(α) | だから | Γ(α) |≦| Γ(α) |+2| α |≦2| Γ(α) |+2| Γ(α) |=2| Γ(α) | である.従って仮定により | Γ(Γ(α)) | と | Γ(α) |+2| α | は比較可能である.
| Γ(Γ(α)) |≦| Γ(α) |+2| α | と仮定すると| Γ(Γ(α)) |≦| Γ(α) | または | Γ(Γ(α)) |≦2| α | でなければならないが,どちらも成立せず,矛盾する.よって | P(α) |=2| α |≦| Γ(α) |+2| α |≦| Γ(Γ(α)) | となり P(α) は整列可能である.
系 一般連続体仮説( κ≦μ≦2κ ならば μ=κ または μ=2κ ) ⇒ 選択公理
定理5 次の命題は( ZF 上)同値
- 選択公理
- μ < 2κ ならば κ と μ は比較可能である.
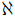 < 2κ ならば κ と
< 2κ ならば κ と 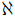 は比較可能である.
は比較可能である.
証明 1 ⇒ 2と2 ⇒ 3は明らか.
(3 ⇒ 1)整列可能定理を示す. X を任意の集合として κ := | X | と置く.κ*≦222κ である. κ* はアレフだから,もし κ*=222κ ならば κ≦222κ=κ* より X は整列可能である.そこで κ* < 222κ だとすると仮定3により κ* と 22κ は比較可能である.もし 22κ≦κ* ならば κ≦22κ≦κ* となり X は整列可能である.そこで κ* < 22κ だとすると再び仮定3により κ* と 2κ は比較可能である.もし 2κ≦κ* ならば κ≦2κ≦κ* となり X は整列可能である.そこで κ* < 2κ だとすると再び仮定3により κ* と κ は比較可能である.このとき κ* の定義から κ≦κ* となり, X は整列可能である.
補題6 κ+1=κ ならば 2κ-κ=2κ
証明 κ=|X| となる集合 X を取る. X∋x |→ { x } ∈P(X) により X⊂P(X) とみなしたとき | P(X) |≦| P(X)\X | を示せばよい.
X に含まれない元 ∞ を一つ取り Y := X∪{ ∞ } と置く. f: P(X)→P(Y)\Y を f(Y) := Y∪{ ∞ } で定める.これは明らかに単射だから | P(X) |≦| P(Y)\Y | である.ここで κ+1=κ だから | Y |=| X | であり,よって | P(Y)\Y |=| P(X)\X | となる.従って | P(X) |≦| P(X)\X | .
定理
選択公理
⇔ κ0, κ1≧![]() 0 とする.次の条件を満たすとき κ0 と κ1 は比較可能である. ある μ≧κ0, κ1 が存在して,任意の ν0, ν1 に対して「 κ0+ν0=κ1+ν1=μ⇒ν0=ν1 」
0 とする.次の条件を満たすとき κ0 と κ1 は比較可能である. ある μ≧κ0, κ1 が存在して,任意の ν0, ν1 に対して「 κ0+ν0=κ1+ν1=μ⇒ν0=ν1 」
証明 ( ⇒ )明らか
( ⇐ )定理の条件3を示す. κ0, κ1 を ![]() 0≦κ0, κ1 なる濃度とする. μ:=2κ0+κ1 と置けば μ≧κ0, κ1 である. κ0+ν0=μ とすると補題6より明らかに ν0=μ である. κ1 についても同様だから,「 κ0+ν0=κ1+ν1=μ⇒ν0=ν1 」が成立する.よって κ0, κ1 は比較可能である.
0≦κ0, κ1 なる濃度とする. μ:=2κ0+κ1 と置けば μ≧κ0, κ1 である. κ0+ν0=μ とすると補題6より明らかに ν0=μ である. κ1 についても同様だから,「 κ0+ν0=κ1+ν1=μ⇒ν0=ν1 」が成立する.よって κ0, κ1 は比較可能である.
定理7 次の命題は( ZF 上)同値
- 選択公理
- 任意の x, y に対して | Pfin(x) | と | Pfin(y) | は比較可能である.
- 任意の x, y に対して | x | と | Pfin(y) | は比較可能である.
- 任意の x, y に対して | x |≦| Pfin(y) | または | y |≦| Pfin(x) | である.
証明 1 ⇒ 2と1 ⇒ 3は明らか.
(2 ⇒ 4) | Pfin(x) |≦| Pfin(y) | ならば | x |≦| Pfin(x) |≦| Pfin(y) | であり, | Pfin(y) |≦| Pfin(x) | ならば | y |≦| Pfin(y) |≦| Pfin(x) | である.
(3 ⇒ 4) | x |≦| Pfin(y) | ならばよい. | Pfin(y) |≦| x | ならば | y |≦| Pfin(y) |≦| x |≦| Pfin(x) | である.
(4 ⇒ 1)整列可能定理を示す. x を集合として y:=Γ(Pfin(x)) と置く.仮定4より | x |≦| Pfin(y) | または | y |≦| Pfin(x) | である. y の定義により | y |![]() | Pfin(x) | だから | x |≦| Pfin(y) | となる. y は順序数だから| y |=| Pfin(y) | である.
| Pfin(x) | だから | x |≦| Pfin(y) | となる. y は順序数だから| y |=| Pfin(y) | である.
順序数・濃度の簡単なまとめの命題11を参照.
故に | x |≦| y | である.よって x は整列可能である.
コメント
コメントはまだありません。