束

PDF版

定義 (L, ≦)を順序集合とする．任意の元x, y∈Lに対し，集合 {x, y}⊂L が上限(=最小上界)と下限(=最大下界)を持つとき，(L, ≦)を束(lattice)という． x∨y := sup{x, y}, x∧y := inf{x, y} と書く．

最大元1と最小元0を持つ束を有界束(bounded lattice)という．
分配律 x∧(y∨z) = (x∧y)∨(x∧z) を満たす束を分配束(distributive lattice)という． (このとき，分配律 x∨(y∧z) = (x∨y)∧(x∨z) も成り立つ．)
任意の部分集合が上限と下限を持つ束Lを完備束(complete lattice)という． A⊂L に対し supA = ∨A = ∨_a∈A a などと表す．下限も同様．

部分集合として空集合を考えれば 0 = ∨∅∈L, 1 = ∧∅∈L である．即ち完備束は有界束．
空でない集合Xに対し，冪集合P(X)は⊂によって束になる．ある X に対する (P(X), ⊂) と同型な束をpowerset latticeという．
空でない位相空間(X, O_X)に対し，O_Xと A_X := (Xの空でない閉集合全体) は包含関係⊂によって束になる．ある X に対する (O_X , ⊂ ) と同型な束をopen lattice， (A_X , ⊂ ) と同型な束をclosed latticeという．

定義(L, ≦)を順序集合とする．

空でない部分集合 F⊊L が次の二条件を満たすとき，Fをフィルター(filter)という．
1. 任意の x, y∈F に対しある z∈F が存在して z≦xかつz≦y となる．
2. x∈Fかつx≦y ならば y∈F
フィルター F⊊L を含むフィルターがF自身しかないとき，Fを極大フィルター(maximal filter)という．
Lを束とする．フィルター F⊊L が

x∨y∈F ⇒ x∈Fまたはy∈F

を満たすとき，Fを素フィルター(prime filter)という．

定理次の命題は(ZF上)同値．

選択公理
二元以上持つ有界束は極大フィルターを持つ
二元以上持つ完備束は極大フィルターを持つ
二元以上持つ分配有界束は極大フィルターを持つ
任意のclosed latticeは極大フィルターを持つ

証明(1 ⇒ 2) Zornの補題による．

(L, ≦)を非自明有界束として集合 X := { F⊂L | Fはフィルター } を考える．⊂で X に順序を入れる．C⊂X を部分全順序集合とする．C = ∅ のときは {1}⊊L が C の上界である．C≠∅ のとき，F := ∪_G∈C G とすればFはフィルターである．

フィルターの定義を確かめる．

(1) x, y∈Fを取る．x∈G₁, y∈G₂となるG₁, G₂∈Cが存在する． (C, ⊂)は全順序だから G₁⊂G₂ または G₂⊂G₁ である．G₁⊂G₂ としても一般性を失わない．このとき x, y∈G₂ となる．G₂ はフィルターだから z≦x, z≦y となる z∈G₂⊂F が存在する．

(2) x∈F, y∈L を取る．x∈G となる G∈C が存在する．G はフィルターだから y∈G⊂F となる．

故にCは上界Fを持つ．故にZornの補題よりXは極大元を持つ．それが極大フィルターである．

(2 ⇒ 3)と(2 ⇒ 4)は明らか．

(3 ⇒ 5)と(4 ⇒ 5)は，closed latticeが非自明完備分配束であることから明らか．

(5 ⇒ 1) ${X_λ}_{λ∈Λ}$ を非空集合の族とする．どのX_λにも含まれない元∞を考え，Y_λ := X_λ∪{∞} とする． A_λ := {Y_λ}∪{ A⊂X_λ | Aは有限集合 } をY_λの閉集合全体としてY_λに位相を定める．直積位相空間 Y := Π_λ∈Λ Y_λ を考える． (∞)_λ∈Λ ∈Y だから，Y は空ではない．よって仮定5よりclosed lattice A_Y は極大フィルターFを持つ． π_λ: Y→ Y_λを射影として F_λ := { A∈A_λ | π_λ^-1(A)∈F } と定める．各F_λは素フィルターである．

A∪B∈F_λとする． F∋π_λ^-1(A∪ B)=π_λ^-1(A)∪π_λ^-1(B) であるからFの極大性によりπ_λ^-1(A)∈Fまたはπ_λ^-1(B)∈Fである．故にA∈F_λまたはB∈F_λ．

Λ₁ := { λ∈Λ | F_λ={Y_λ} }，Λ₂ := Λ＼Λ₁とする．λ∈Λ₂とすると，A∈A_λとなる有限集合 A⊂X_λ がある．故に素フィルターの性質から {x_λ}∈F_λ となるx_λ∈X_λが唯一つ存在することが分かる．よって(x_λ)_λ∈Λ₂∈Π_λ∈Λ₂X_λが取れる．つまり，Λ₂=Λ (即ちΛ₁=∅ ) を示せば証明が終わる． y=(y_λ )_λ∈Λ ∈Y を

λ∈Λ₁のとき y_λ := ∞
λ∈Λ₂のとき y_λ := x_λ

で定義する．λ∈Λとして，U⊂Y_λをy_λの開近傍とする． π_λ^-1(U)はFの全ての元と交わる．

任意のB∈Fを取る．するとyの任意の近傍はBと交わる． FはA_Yのフィルターだから，B∈Fは閉集合．従ってy∈Bとなる．Bは任意だったから y ∈ ∩F := ∩_B∈F B である． ∩Fは閉集合だから，cl({y})⊂∩F となる( cl は閉包)．また cl({y}) = cl(Π_λ∈Λ {y_λ})⊂Π_λ∈Λ cl({y_λ}) である．

λ∈Λ₁のとき Z_λ := Y_λ
λ∈Λ₂のとき Z_λ := {x_λ}

と置けば cl({y_λ})=Z_λ だから cl({y})=Π_λ∈Λ Z_λ となる．

Λ₁≠∅と仮定する．μ∈Λ₁とz_μ∈X_μを取り，閉集合 {z_μ}×Π_λ≠μ Z_λ⊂Y で生成されるA_Yのフィルターを考える．これは明らかにFより真に大きいので，極大性に矛盾する．故にΛ₁=∅である．

定義完備束Lがcompletely distributive
⇔任意の族 ${X_λ}_{λ∈Λ}$ と任意の写像 x: ∪_λ∈Λ ({λ}×X_λ)→L に対し

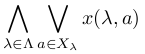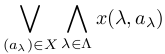
$∧_{λ∈Λ}∨_{a∈X_λ}x(λ, a)$ = $∨_{(a_λ)∈X}∧_{λ∈Λ}x(λ, a_λ)$

が成立する(ただし，X := $Π_{λ∈Λ}X_λ$ と置いた)．

定理次の命題は(ZF上)同値．

選択公理
全順序な完備束はcompletely distributive
powerset latticeはcompletely distributive
完備束 2 := {0, 1} はcompletely distributive

証明(1 ⇒ 2) Lを全順序な完備束として，集合族 ${X_λ}_{λ∈Λ}$ と写像 x: ∪_λ∈Λ ({λ}×X_λ)→L を取る． X := $Π_{λ∈Λ}X_λ$ と置く．

まず≧を示す．任意の(a_λ)∈Xを取る．各λ∈Λについて 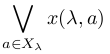$∨_{a∈X_λ}x(λ, a)$ ≧x(λ, a_λ)．故に

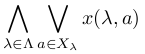$∧_{λ∈Λ}∨_{a∈X_λ}x(λ, a)$ ≧∧_λ∈Λ x(λ, a_λ)

(a_λ)∈X は任意だったから

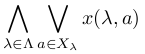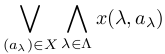
$∧_{λ∈Λ}∨_{a∈X_λ}x(λ, a)$ ≧ $∨_{(a_λ)∈X}∧_{λ∈Λ}x(λ, a_λ)$

が示された．次に≦を示す．

y:=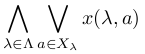 $∧_{λ∈Λ}∨_{a∈X_λ}x(λ, a)$

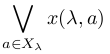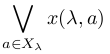と置く．λ∈Λとすると $∨_{a∈X_λ}x(λ, a)$ <yでない．よってLは全順序だから $∨_{a∈X_λ}x(λ, a)$ ≧yである．故にあるa∈X_λが存在してx(λ, a)<yでない． Lは全順序だからx(λ, a)≧yである．即ち，A_λ := { a∈X_λ | x(λ, a)≧y } とすると任意のλ∈Λに対してA_λ≠∅となる．選択公理によりΠ_λ∈Λ A_λ≠∅，即ち元(b_λ)∈Π_λ∈Λ A_λが存在する． A_λの定義から，各λ∈Λに対しx(λ, b_λ)≧ yとなる．このとき

y≦∧_λ∈Λ x(λ, b_λ)≦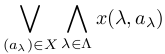 $∨_{(a_λ)∈X}∧_{λ∈Λ}x(λ, a_λ)$

だからyの定義により

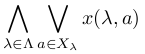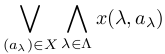
$∧_{λ∈Λ}∨_{a∈X_λ}x(λ, a)$ ≦ $∨_{(a_λ)∈X}∧_{λ∈Λ}x(λ, a_λ)$

が示された．

(1 ⇒ 3) 選択公理から「∩, ∪の分配律」が従うことから分かる．

これは実は同値である．∪∩の分配法則を参照．

(2 ⇒ 4) 2 が全順序であることから明らか．

(3 ⇒ 4) 2 = {0, 1} = {∅, {∅}} = P({∅}) から明らか．

(4 ⇒ 1) ${X_λ}_{λ∈Λ}$ を非空集合の族とする． X := $Π_{λ∈Λ}X_λ$ と置く． x: ∪_λ∈Λ({λ}×X_λ)→2 を x(λ, a) := 1 で定めれば

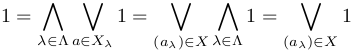
$1=∧_{λ∈Λ}∨_{a∈X_λ}1=∨_{(a_λ)∈X}∧_{λ∈Λ}1=∨_{(a_λ)∈X}1$

∨_a∈∅ x_a = 0 だから，最右辺が1になる為には X≠ ∅ でなければならない．

(名無し) | 2014年5月21日 01:44

ぷよぷよだけでなく集合論でも助けになりました！
ありがとうございました！

束

コメント

コメントする