Bernsteinの定理
Cantor-Bernstein-Schroederの定理
単射 f: X→Y と単射 g: Y→X が存在するならば， 全単射 h: X→Y が存在する．
即ち，|X|≦ |Y|かつ|Y|≦ |X|ならば|X|=|Y|である． この定理は選択公理を使わずに(ZFで)証明できる．
以下，この命題をCBSと書くことにする．
証明
f, gのどちらかが全射ならば明らかだから，どちらも全射でないとする．以下のように集合を定義する．
A := ∪_{n=0}^{∞}X_n, B := X＼ A
C := ∪_{n=0}^{∞}Y_n, D := Y＼ C
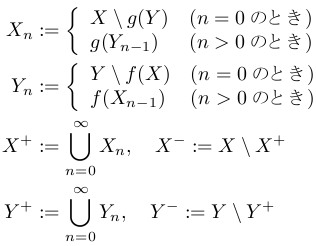
f, gが単射なので，異なる非負整数m, nに対しX_m∩X_n = ∅, Y_m∩Y_n = ∅ である． またX = A∪B = (∪X_n)∪B, Y = C∪D = (∪Y_n)∪D となる．
f(A) = f(∪_{n=0}^∞X_n) = ∪_{n=1}^∞Y_n かつ
f(X) = Y＼Y_0 = (∪_{n=1}^{∞}Y_n)∪D だから，
f(B) = D である．そこで h: X→Y を
x∈X_{2n} のとき h(x) := f(x)
x∈X_{2n+1} のとき h(x) := g-1(x)
x∈B のとき h(x):= f(x)
と定義すれば，これは明らかに全単射である．
この定理から，すぐに「双対版」が思いつく．
双対Bernsteinの定理
全射 f: X→Y と全射 g: Y→X が存在するならば， 全単射 h: X→Y が存在する．
この命題をCBS*で表すことにする． 選択公理を使えば，CBS*はCBSから簡単に導くことができる．
選択公理は「全射の右逆写像の存在」と同値．即ち
選択公理
⇔ 任意の全射 F: X→Y に対しある単射 G: Y→X が存在してFG=idY．
(⇒)Fの全射性より族 { F-1(y) }_{y∈Y} は非空集合の族なので 選択関数 G: Y→∪_{y∈Y}F-1(y)=X が存在する．このとき明らかに FG=idY．
(←)
を非空集合の族とする．各X_λは互いに素としてよい．
このとき F: 
→Λを
F(x) := (x∈X_λとなるλ) で定める．Fは全射だから仮定より
FG=idY となる G: Λ→が存在する．
このときGが明らかに選択関数である．
そこで u: Y→X, v: X→Y を全射f, gの右逆写像として v, uにCBSを適用すれば全単射 h: X→Y が得られる．
つまりCBS*はZFCで証明可能． しかし，CBS*はZF(更に言えばZF+DC)で証明できないことが知られている．
藤田博司さんがそのことについて書かれています． http://www.math.sci.ehime-u.ac.jp/~fujita/notes.jp.htmlにあるPDF双対ベルンシュタイン定理についてを参照． また，ZFで「CBS*⇒選択公理」が成立するかどうかは未解決問題らしいです．
CBSでのhに条件を加えた命題を考える．
命題
単射 f: X→Y と単射 g: Y→X が存在するならば， 全単射 h: X→Y で h⊂f∪g-1 を満たすものが存在する．
h⊂f∪g-1 はf, g-1, hを X×Y の部分集合とみなして考えるということ．
この命題をCBS+で表すことにする．当然これの双対版も考えられます．
命題
全射 f: X→Y と全射 g: Y→X が存在するならば， 全単射 h: X→Y で h⊂f∪g-1 を満たすものが存在する．
この命題をCBS+*で表すことにする．
CBSの証明の中で構成した全単射hは明らかに h⊂f∪g-1 を満たす． 故にCBS+はZFで証明可能である． 一方CBS+*については次が成り立つ．
定理
選択公理⇔ CBS+*
証明
(⇒)f: X→Y と g: Y→X を全射とする． 選択公理によりf, gの右逆写像 u: Y→X, v: X→Y が存在する． 即ち fu = idY, gv = idX． このとき u-1⊂f, v⊂g-1 である．
(i) u-1⊂f について
任意の<x, y>∈u-1を取る．u(y)=xである．fu=idYより
y=fu(y)=f(x)だから<x, y>∈ fである．よってu-1⊂f．
(ii) v⊂g-1について
任意の<x, y>∈vを取る．v(x)=yである．gv=idXより
x=gv(x)=g(y)だから<x, y>∈g-1である．よってv⊂g-1．
単射 v: X→Y と単射 u: Y→X にCBS+を適用して 全単射 h: X→Y で h⊂v∪u-1 を満たすものを取れば h ⊂ v∪u-1 ⊂ f∪g-1．
(←)全射 f: X→Y の右逆写像の存在を示す．
Z := { 0 }∪Y∪(X×N) として写像 k: Z→Z を次で定める．
k(0) := 0
k(y) := 0 (y∈ Y)
k(<x, 0>) := f(x) (x∈ X)
k(<x, n+1>) := <x, n> (x∈ X, n∈N)
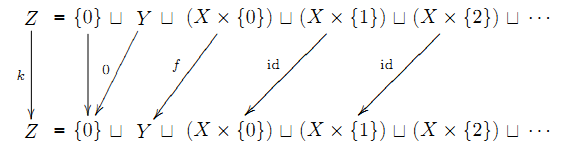
明らかにkは全射である．そこで全射 k: Z→Z と全射 k: Z→Z にCBS+*を適用して 全単射 h: Z→ Z で h⊂k∪k-1 を満たすものを取る． 写像 h|Y を考える．
(i) h|Y⊂k-1のとき
y∈Y に対し h(y)∈k-1(y) となる．
よって kh(y) = y．また，kの定義より k-1(Y) = X×{ 0 } だから
h(y)∈k-1(y)⊂X×{0}である．故に，ある写像
g: Y→X を使って h(y)=<g(y), 0> と書ける．このとき任意のy∈Yに対し
y = kh(y) = k(<g(y), 0>) = f(g(y)) = fg(y)
即ちgはfの右逆写像．
(ii) h|Y⊂k-1でないとき
h⊂k∪k-1 だから
あるa∈Yが存在してh(a)=k(a)である．
このときkの定義からh(a)=0となる．
hは全単射だったから，実はこのようなaは唯一つしか存在しない．
故に A := Y＼{ a } と置けば h|A⊂k-1 となる．
そこでAについて(i)と同様の議論をすれば
写像g: A→X で fg=idA となるものが取れる．
そこで元 b∈f-1(a) を一つ取り g(a) := b として g: Y→X へ拡張すれば
明らかにgがfの右逆写像である．
系
選択公理
⇔全射 f: X→X に対し
全単射 h: X→X で h⊂f∪f-1を満たすものが存在する．
参考文献
- Bernhard Banaschewski and Gregory H. Moore, The dual Cantor-Bernstein theorem and the partition principle
コメント
コメントはまだありません。