定義

• X=Y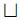Z ⇔ X=Y∪Z かつ Y∩Z = ∅

• X, Y⊂R³ を有界部分集合とする．このときある r = (a, b, c)∈R³ が存在して X∩(Y+r) = ∅　( Y+r := { (x+a, y+b, z+c) | (x, y, z)∈Y } ) とできる．この r を使って X⊕Y := X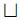(Y+r) と定める．

  もちろんこの X⊕Y はrの取り方によるが，以下ではrの取り方は特に関係ない場面でしか X⊕Y は使用しない．

G₃ を R³ の回転と平行移動がなす群とする．

定義 X, Y⊂R³ が分割合同 (X～Yで表す)
⇔ あるn∈NとX_i, Y_i⊂R³, σ_i∈G₃ (0≦i≦n)が存在して X = X₀…X_n, Y = Y₀…Y_n, Y_i = σ_iX_i．

命題

1. 分割合同～は同値関係である．
2. X₀～Y₀, X₁～Y₁ ならば X₀⊕X₁～Y₀⊕Y₁ である．特に X₀∩X₁ = ∅, Y₀∩Y₁ = ∅ ならば X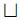₀X₁～Y₀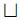Y₁となる．

Banach-Tarskiの定理 B := { (x, y, z)∈R³ | x²+y²+z²≦1 } とすればB～B⊕B．

これを証明するために，まず分割合同の例を二つあげる．

例 適当な方法で S¹ = { x∈C | |x|=1 }⊂R³とみなす．

X := { e^n√-1 | n∈N }, Y := S¹＼X とする．原点を中心とした1ラジアンの回転をσとすればσX = { e^n√-1 | n>0 } = X＼{1} であるから S¹ = XY ～ (X＼{1})Y = S¹＼{1}となる．即ち「円周から一点を抜いた集合」は円周と分割合同である．

例 O∈R³ を原点として，(適当に縮小した)S¹を B の中に O∈B∩S¹ となるように埋め込めば B = (B＼S¹)S¹ ～ (B＼S¹)(S¹＼{O}) = B＼{O} だから「球体から原点を抜いた集合」は球体と分割合同である．

これらの例から分かるように，分割合同というのは(物理的には)かなり変な分割の仕方も許している． また，次のことが分かる．

命題 S²～S²⊕S² とする． このとき B～B⊕B

証明 S² = X₀…X_n, S²⊕S² = Y₀…Y_n, Y_i=σ_iX_i とする．X⊂S²に対してh(X) := { tx | x∈X, 0<t≦1 } とすれば h(S²) = B＼{O} となり，B＼{O} = h(X₀)…h(X_n), B＼{O}⊕B＼{O} = h(Y₀)…h(Y_n), h(Y_i) =σ_ih(X_i) である．故に B～B＼{O}～B＼{O}⊕B＼{O}～B⊕B である．

故に，後は S²～S²⊕S² を示せばよい．

定義 Xを集合とする．有限列の集合{ x₁… x_n | n∈N, x_i∈X∪X^-1 } に積を列の結合 (x₁… x_n)・(y₁… y_m) := x₁…x_ny₁…y_m で定めるとこれは群になる(ただし，x と x^-1 が隣り合ったときはキャンセルする．また空文字列を単位元とみなす)．これを X で生成される自由群という．

二元集合{ρ, τ}で生成される自由群を F₂ と書く．

命題 W(σ) := { x₁…x_n∈F₂ | x₁=σ} と置けば

F₂ = {1}W(ρ) W(ρ^-1)W(τ)W(τ^-1)
= W(ρ)ρW(ρ^-1)
= W(τ)τW(τ^-1).

Banach-Tarskiの証明において，選択公理を使用するのは次の部分だけである．

命題1 選択公理を仮定する．F₂ が集合 X⊂R³ に自由に作用しているとき，ある A, B⊂X が存在して AB⊂X, X～A～B

群GのXへの作用が自由である
⇔ 任意のg∈G, x∈Xに対して「gx=x⇒g=e」

証明 X に同値関係 R を「xRy ⇔ あるσ∈F₂が存在してy=σx」で定める．選択公理により商集合 X/R の完全代表系 M を取ることができる．すると作用が自由であるから X = _σ∈F2σM となる．

A₀ := _σ∈W(ρ)σM, A₁ := _{σ∈W(ρ^-1)}σM, A := A₀ A₁
B₀ := _σ∈W(τ)σM, B₁ := _{σ∈W(τ^-1)}σM, B := B₀ B₁

と置けば，X = A₀ρA₁ = B₀τB₁⊃A₀A₁B₀B₁ であるから AB⊂X かつ X～A～B となる．

定義 A, B⊂R³ に対して二項関係を次のように定める．

AB ⇔ ある B'⊂B が存在して A～B'

Banach-Bernstein-Schröderの定理 AB かつ BAならば A～B．

証明 A～Bのとき，全単射 f: A→B で「任意の A'⊂A に対して A'～f(A') 」を満たすものが取れることに注意しておく．

AB かつ BA とする．ある A'⊂A と B'⊂B が存在して A～B' かつ B～A' である．よって全単射 f: A→ B' と g: A'→B で先の条件を満たすものが取れる．A₀ := A＼A', A_n+1 := g^-1(f(A_n)), X := _n=0^∞A_nと定める．

X⊂A, A＼X⊂A' だから X～f(X), A＼X～g(A＼X) である．従って A = X(A＼X)～f(X)g(A＼X) = B が分かる．

命題 R³の原点を中心とする回転がなす，G₃の部分群をSO(3)で表す． SO(3)はF₂と同型な部分群を持つ．

証明 θ=arccos(1/3)として，R³のz軸を軸とするθラジアンの回転をρ，x軸を軸とするθラジアンの回転をτとすればρ, τが生成するSO(3)の部分群はρ, τが生成する自由群F₂であることが分かる．

この命題によりF₂⊂SO(3)とみなせば，F₂は球面S²に作用する．各元σ∈F₂の不動点x∈S²は丁度2つある．よって D := { x∈S² | あるσ∈F₂が存在してσ x=x } は可算集合である．このとき F₂ は X := S²＼D に自由に作用する．故に命題1からある A, B⊂X, A∩B = ∅ が存在して A～X かつ B～X である．A, B の取り方から X～B⊂X＼A⊂X，即ち XX＼A かつ X＼AX であるからBanach-Bernstein-Schroederの定理により X＼A～X が分かる．改めて B := X＼A と書き直せば X = AB～A～Bが分かる．即ち，S²＼D～(S²＼D)⊕(S²＼D)である．

命題 S²～ S²⊕S²

証明 σ∈SO(3)で D, σ D, σ²D, …が互いに素となるものが存在する．

このとき Y := S²＼(∪_n=0^∞σⁿD) と置けば S² = Yl(∪_n=0^∞σⁿD)～Y(∪_n=0^∞σ^{n+1}D) = S²＼D である．故に S²～S²＼D～(S²＼D)⊕(S²＼D)～S²⊕S² となる．

以上により次が証明された．

Banach-Tarskiの定理 B～B⊕B

強Banach-Tarskiの定理 内部が空でない有界部分集合 X, Y⊂R³ に対して X～Y．

証明 仮定によりある球体 K, L が存在して X⊂K かつ L⊂Y となる．n∈Nを十分大きく取り，L のn個のコピー L₁, …, L_n で K を被覆する．このとき X⊂KL₁⊕…⊕L_n～L⊂Y より XY が分かる．同様にして YX だから X～Y となる．

ところで，Banach-Tarskiの定理の証明で選択公理を使っている部分は命題1のみであった．実は命題1はHahn-Banachの定理から導かれる．

定義 Bをブール代数とする．
μ: B→[0, 1] が B 上の有限加法的測度
⇔ μ(1)=1 かつ「x∧y=0 ⇒ μ(x∨y)=μ(x)+μ(y)」

定理 Hahn-Banachの定理
⇔ 任意のブール代数 B について B 上の有限加法的測度が存在する．

定理 Hahn-Banachの定理 ⇒ 命題1

証明 命題1の証明の X/R を考える．U∈X/R に対してブール代数 B_U := P(U) を考え，ブール代数の直和 B := ⊕_U∈X/RB_U を取る．i_U: B_U→B を標準埋込とする．Hahn-Banachの定理により，B 上の有限加法的測度μが取れる．μ_U := μi_Uと置く．V(σ) := { x₁…x_n∈F₂ | x_n=σ } として

X₁ := { x∈X | μ_[x](V(ρ)x) > 1/2 }
X₂ := { x∈X | μ_[x](V(τ)x) > 1/2 }
X₃ := { x∈X | μ_[x](V(ρ^-1)x) > 1/2 }
X₄ := { x∈X | μ_[x](V(τ^-1)x) > 1/2 }
Y₁ := X＼(ρX₁∪τX₂)
Y₂ := X＼(ρ^-1X₃∪τ^-1X₄)

と定める．X = ρX₁∪τX₂∪ρ^-1X₃∪τ^-1X₄である．

従って Y₁∩Y₂ = ∅ である．また明らかに X₁, X₂, X₃, X₄ は互いに素である．

Y₁ と X₁ は互いに素である．

同様にして i=1, 2, j=1, 2, 3, 4 に対して Y_i∩X_j = ∅ が分かる．

X₂'⊂X₂, X₄'⊂X₄ を ρX₁∪τX₂=ρX₁τX₂', ρ^-1X₃∪τ^-1X₄=ρ^-1X₃τ^-1X₄' となるように取る．A = X₁X₂'Y₁, B := X₃X₄'Y₂ と置けば A B⊂X かつ X～A, X～B である．

系 Hahn-Banachの定理⇒Banach-Tarskiの定理

Banach-Tarskiの証明から得られる B の分割の仕方を見ると，この分割が物理的に可能であったとしても，物理的に移動させることが不可能のようにみえる．そこで，《物理的な移動まで含めた分割合同》というものを考えてみる．

定義 X, Y⊂R³とする．
XY ⇔ n∈N, X_i, Y_i⊂R³，連続写像γ_i: [0, 1]→G₃　(0≦i≦n) が存在して以下を満たす．

• X = X₀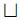…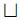X_n
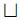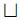• Y = Y₀…Y_n
• γ_i(0) = id_R³
• Y_i = γ_i(1)X_i
• i≠jならば，任意の t∈[0, 1] に対してγ_i(t)X_i∩γ_j(t)X_j = ∅．

命題 は同値関係である．

定義 u∈R³に対してσ_u∈G₃を σ_u(x) = x+u で定める．

命題 X, Y⊂R³を有界部分集合とし，u, v∈R³を X∩σ_uY = ∅, X∩σ_vY = ∅ となるように取る．このときXσ_uY Xσ_vY

証明 略 (PDF版参照。こっちはそのうち書きます)

命題X₀, X₁⊂R³を互いに素な有界集合， σ₀, σ₁∈G₃, σ₀X₀∩σ₁X₁=∅とするとき X₀ X₁σ₀X₀σ₁X₁．

証明 略 (PDF版参照)

命題 内部が空でない有界部分集合 X, Y⊂R³に対してXY

証明 強Banach-Tarskiの定理によりある分割 X = X₀…X_n, Y = Y₀…Y_n とσ_i∈G₃ が存在してσ_iX_i = Y_i となる．故に前命題を繰り返し使用して

X = X₀…X_nσ₀X₀…σ_nX_n = Y.