選択公理と同値な命題リスト
ZF (基礎の公理を含む) で考えています.
選択公理
- 任意の集合は選択関数を持つ (選択公理)
- 非空集合の直積は空でない
- 互いに素な非空集合の族は選択集合を持つ
- 一般化された従属選択公理: ∀αDC(α)
- 任意の X に対し MC(X, m) (m≧2は固定された整数)
- ある m≧2 が存在して任意の X に対し MC(X, m)
- 任意の X に対しある m≧2 が存在して MC(X, m)
- 任意の X に対し MC(X,
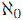 ) (the Axiom of Multiple Choice)
) (the Axiom of Multiple Choice) - the Axiom of Odd Choice
- the Axiom of Even Choice
- 集合 X が「任意の x∈X に対し |x|≧2 」を満たすとするとき, X 上の写像 f が存在して,任意の x∈X に対し f(x) ⊊ x, 0<|f(x)|<∞ を満たす.
整列可能定理
- 任意の集合は整列可能 (整列可能定理)
- 任意の全順序集合は整列可能
- 整列順序集合の冪集合は整列可能
- 選択関数を持つ集合は整列可能
- 任意の集合 X に対し WO(X, m) (m≧2は固定された整数)
- ある m≧2 が存在して任意の集合 X に対し WO(X, m)
- 任意の集合 X に対しある m≧2 が存在して WO(X, m)
- 任意の集合 X に対し WO(X,
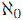 )
)
極大原理
- 空でない順序集合が「任意の部分全順序集合が上界を持つ」を満たすならば極大元を持つ (Zornの補題)
- 空でない順序集合が「任意の部分全順序集合が上限を持つ」を満たすならば極大元を持つ
- 空でない順序集合が「任意の部分整列順序集合が上界を持つ」を満たすならば極大元を持つ
- 空でない集合x上の推移的関係Rが 「xの部分集合でRによって全順序付けされるものには上界が存在する」を満たすならば,xの極大元が存在する.
- 空でない集合x上の推移的関係Rが 「xの部分集合でRによって整列順序付けされるものには上界が存在する」を満たすならば,xの極大元が存在する.
- 集合x上の推移的関係Rに対し,Rによって全順序付けされる極大部分集合が存在する
- 任意の集合xを⊂で順序集合とみなしたとき,xは極大鎖を持つ
- 任意の集合xを⊂で順序集合とみなしたとき,xが「鎖y⊂xに対し,∀a∈y(a⊂b)となるような元b∈xが存在する」を満たすならば,xの極大元が存在する
- 有限性をもつ非空集合xは(⊂に関する)極大元をもつ (Tukeyの補題)
- 任意の前順序集合(x, ≦)は極大鎖を持つ
- 任意の順序集合(x, ≦)は極大鎖を持つ (Hausdorff's Maximal chain Condition)
- 任意の順序集合(x, ≦)の任意の鎖は,xのある極大鎖に含まれる
- 任意の木(T, ≦)は極大鎖を持つ
- 任意の前順序集合(x, ≦)は極大反鎖を持つ
- 任意の順序集合(x, ≦)は極大反鎖を持つ (Kurepa's Maximal Antichain Condition)
- 任意の集合x,正整数n,n項関係R⊂x^nに対し,y^n⊂Rとなる極大なy⊂xが存在する
- 順序集合Xが「下の条件(*)を満たす任意のA⊂Xが上界を持つ」を満たすならば,Xは極大元を持つ.
(*) 任意の元x, y∈Aに対し { x, y }⊂A はAに上界を持つ.
- M(1)
- M(2)
- M(3)
- M(4)
- M(5)
- N(D)
- N(Dc)
- N(K)
- N(J)
- N(Jc)
集合
任意の
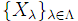 と,
定義域が∪_{λ∈Λ}({λ}×Xλ)である写像Aに対し
と,
定義域が∪_{λ∈Λ}({λ}×Xλ)である写像Aに対し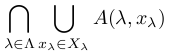 =
=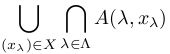
任意の
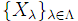 に対し
に対し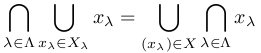
- 全射 f: X→Y と全射 g: Y→X が存在するならば,全単射 h: X→Y で h⊂f∪g-1 を満たすものが存在する
- 全射 f: X→X に対し全単射 h: X→X で h⊂f∪f-1を満たすものが存在する
- 非空集合の族
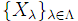 で全てのXλの濃度が等しいもの,に対し直積集合
で全てのXλの濃度が等しいもの,に対し直積集合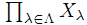 は空でない.
は空でない. - 集合の順序対からなる族 { <Xλ, Yλ> }λ∈Λが,各λ∈Λに対し |Xλ| = |Yλ| を満たしているとする.このとき写像の族 {fλ}λ∈Λ で,「各λ∈Λに対し fλ: Xλ→Yλ は全単射」を満たすものが存在する.
- 非空集合の族
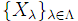 は全てのXλの濃度が等しいとする.このとき写像の族{ f_{λ, μ} }_{λ, μ∈Λ}で,「各λ, μ∈Λに対し f_{λ, μ}: Xλ→X_μ は全単射」を満たすものが存在する.
は全てのXλの濃度が等しいとする.このとき写像の族{ f_{λ, μ} }_{λ, μ∈Λ}で,「各λ, μ∈Λに対し f_{λ, μ}: Xλ→X_μ は全単射」を満たすものが存在する. - 任意の X≠∅ と写像 F: X→Y に対して写像 G: Y→X が存在して FGF = F となる.
- 任意の全射 F: X→Y に対して,ある G: Y→X が存在して FG = id_Y.
- 任意の集合は射影的.
- 任意の集合Xに対して,射影的な集合Yが存在して X⊂Y.
- 二項関係 R⊂X×Xが ∀x∈X∃y∈X xRy を満たすとき,写像 f: X→X で∀x∈X xRf(x) を満たすものが存在する.
- 任意の族
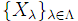 に対し,
互いに交わらない集合の族 {Yλ}λ∈Λ で
Yλ⊂ Xλ, ∪_{λ∈Λ}Yλ=∪_{λ∈Λ}Xλ
を満たすものが存在する
に対し,
互いに交わらない集合の族 {Yλ}λ∈Λ で
Yλ⊂ Xλ, ∪_{λ∈Λ}Yλ=∪_{λ∈Λ}Xλ
を満たすものが存在する - 任意の集合は射影的
群・加群
- 任意の非空集合は群構造を持つ
- strong Nielsen-Schreierの定理
- 任意の可換環 R とR-加群 M に対して次が成り立つ.
任意のイデアル I⊂R と任意の準同型 φ: I→ M に対して
ある準同型 ψ: R→M が存在して ψ|I=φ となる.
⇒ Mが入射的 - 任意の単項イデアル整域 R に対して,可除R-加群は入射的
- 可除アーベル群は入射的
- 任意の環 R とR-加群の族 { Mλ }λ∈Λ に対して
全てのλ∈Λについて Mλ が射影的 ⇒ M :=⊕λ∈Λ Mλ が射影的
- 任意の環 R に対して,任意の自由R-加群は射影的
- 任意の自由アーベル群は射影的
- ある環 R が存在して,任意の自由R-加群は射影的
環
- 右単位的環は極大左イデアルを持つ
- 左単位的環は極大右イデアルを持つ
- 右単位的環は極大イデアルを持つ
- 左単位的環は極大イデアルを持つ
- 右単位的環の真の左イデアルはある極大左イデアルに含まれる
- 左単位的環の真の右イデアルはある極大右イデアルに含まれる
- 右単位的環の真のイデアルはある極大イデアルに含まれる
- 左単位的環の真のイデアルはある極大イデアルに含まれる
- 冪等元(≠0)を持つ環は極大左イデアルを持つ
- 冪等元(≠0)を持つ環は極大右イデアルを持つ
- 左半中心冪等元(≠0)を持つ環は極大イデアルを持つ
- 右半中心冪等元(≠0)を持つ環は極大イデアルを持つ
- 単位的可換環は極大イデアルを持つ
- 一意分解整域は極大イデアルを持つ
- 任意の環は部分直既約な環の部分直積である
- 任意の一意分解整域は部分直既約な環の部分直積である
- 任意の環Rに対して,ある部分直既約な環S≠0と全射環準同型R→Sが存在する
- 任意の一意分解整域Dに対して,ある部分直既約な環S≠0と全射環準同型D→Sが存在する
線型空間
- 任意の線型空間は基底を持つ
- 線型空間の生成系は基底を含む.
- Q-線型空間の生成系は基底を含む.
- F2-線型空間の生成系は基底を含む.
- 線型空間は入射的
- 線型空間は射影的
- 基底を持つ線型空間は射影的
- 任意の一般化線型空間に基底が存在する
束
- 任意の有界束は極大フィルターを持つ
- 任意の完備束は極大フィルターを持つ
- 任意の分配有界束は極大フィルターを持つ
- 任意のclosed latticeは極大フィルターを持つ
- 全順序な完備束はcompletely distributive
- powerset latticeはcompletely distributive
- 完備束 2 := {0, 1} はcompletely distributive
解析学
- Vを実線型空間,W⊂Vを部分空間,S⊂Vを部分集合とする. p: V→Rを劣線型汎関数とし,線型汎関数f: W→Rはf≦Wpを満たすとする.このとき前順序集合(Z(p, f), ≦S)の極大元が存在する.
- Vを実線型空間,W⊂Vを部分空間として,p: V→Rを劣線型汎関数とする. f: W→Rを線型汎関数とし,f≦Wpを満たすとする. このときZ(p, f)はextrime pointを持つ.
- 「実ノルム空間の双対空間」の単位球体はextrime pointを持つ
位相空間
- コンパクト空間の直積はコンパクト (Tychonoffの定理)
- コンパクトかつT1な空間の直積はコンパクト
- 開集合が有限個な空間の直積はコンパクト
- 互いに同相なコンパクト空間の直積はコンパクト
- 互いに同相な,開集合が丁度3個ある空間の直積はコンパクト
- 任意の位相空間の族
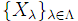 と
部分集合Aλ⊂Xλに対し
cl(Π_{λ∈Λ}Aλ)⊃Π_{λ∈Λ}cl(Aλ)
と
部分集合Aλ⊂Xλに対し
cl(Π_{λ∈Λ}Aλ)⊃Π_{λ∈Λ}cl(Aλ) - コンパクト ⇒ Alexandroff-Urysohn-コンパクト
- コンパクト ⇔ Alexandroff-Urysohn-コンパクト
- Alexandroff-Urysohn-コンパクト空間の有限和はAlexandroff-Urysohn-コンパクト
- 開集合が有限個の位相空間はAlexandroff-Urysohn-コンパクト
- 密着位相空間の有限和はAlexandroff-Urysohn-コンパクト
- Alexandroff-Urysohn-コンパクト空間の直積はAlexandroff-Urysohn-コンパクト
- Alexandroff-Urysohn-コンパクト空間の有限直積はAlexandroff-Urysohn-コンパクト
- 開集合が有限個な空間の直積はAlexandroff-Urysohn-コンパクト
- 有限離散位相の直積はAlexandroff-Urysohn-コンパクト
- 「{0, 1}に離散位相を入れた空間」の直積はAlexandroff-Urysohn-コンパクト
- Tychonoff-コンパクト空間はAlexandroff-Urysohn-コンパクト
- [0, 1]の直積はAlexandroff-Urysohn-コンパクト
- スーパーコンパクト空間の直積はスーパーコンパクト
- 任意の位相空間は極大なT0部分空間を持つ
- 任意の位相空間は極大なT1部分空間を持つ
- 任意の位相空間は稠密なT0部分空間を持つ
- 任意の位相空間はcodenseなT0部分空間を持つ
- 任意の位相空間はthickなT0部分空間を持つ
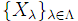 を位相空間の族とし,
{Aλ}λ∈Λは任意のλ∈Λについて
∅≠ Aλ⊂ Xλを満たすとする.このとき
を位相空間の族とし,
{Aλ}λ∈Λは任意のλ∈Λについて
∅≠ Aλ⊂ Xλを満たすとする.このとき
Πλ∈ΛAλ⊂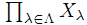 が閉集合 ⇒ 任意のλ∈Λ に対しAλ⊂ Xλが閉集合
が閉集合 ⇒ 任意のλ∈Λ に対しAλ⊂ Xλが閉集合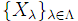 を位相空間の族とし,
{Aλ}λ∈Λは任意のλ∈Λについて
∅≠ Aλ⊂ Xλを満たすとする.このとき
を位相空間の族とし,
{Aλ}λ∈Λは任意のλ∈Λについて
∅≠ Aλ⊂ Xλを満たすとする.このとき
Πλ∈ΛAλ⊂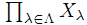 が閉集合 ⇒ あるλ∈Λ に対しAλ⊂ Xλが閉集合
が閉集合 ⇒ あるλ∈Λ に対しAλ⊂ Xλが閉集合