線型空間 V に基底 B があったとき，これの濃度 |B| を V の次元というが，これには一意性がある．即ち次の命題が知られている．

命題 B, C⊂V が共に V の基底であるとき，|B| = |C|．

ところが，この命題の証明には選択公理が必要なのである． それを示すため，以下のようにpermutationモデルを構成する．

アトム全体の集合 A が A=B∪C，B=∪_n=0^∞B_n，C=∪_n=0^∞C_n，B_n= { b_n1, …, b_n6 }，C_n= { c_n1, …, c_n6 } と書けているとする．置換 α_i, β_i, γ_i∈S₆ を以下のように定める．

α₁ = (12)(34)(5)(6)，　α₂ = (12)(34)(5)(6)，
β₁ = (13)(24)(5)(6)，　β₂ = (12)(3)(4)(56)，
γ₁ = (14)(23)(5)(6)，　γ₂ = (1)(2)(34)(56)

α∈Aut(A) を B_n 上 α₁ のように， C_n 上 α₂ のように作用するものとする． β, γ∈Aut(A) も同様に定める．

G= { g∈Aut(A) | 各n∈Nについて g|_Bn∪Cn=1, α, β, γ }

として I := P_fin(A) によりpermutationモデル U を取る．X を B を基底とする実線型空間，Y を C を基底とする実線型空間とする．

命題 X ≅ Y である．

証明 X_n, Y_n を B_n, C_n を基底とする 6 次元実線型空間とする．線型写像 f_n: X_n→Y_n を，次の行列により定める．

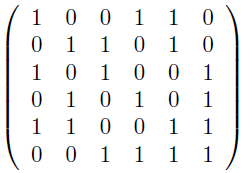
この行列の行列式は -8 となるので， f_n は同型である． X ≅ ⊕ X_n ， Y ≅ ⊕ Y_n だから， f_n から同型 f: X→Y が得られる．また計算すれば α₂(f(α₁^-1(x))) = f(x)，β₂(f(β₁^-1(x))) = f(x)，γ₂(f(γ₁^-1(x))) = f(x) となることがわかる．故に任意の g∈G に対して g(f) = f である．よって f∈U ．

命題 |B|≠|C| である．

証明 ₀≦|B| かつ ₀|C| を示せばよい．

まず f: ω→B を f(n) := b_n6 で定める．このとき明らかに f∈U で f は単射だから ₀≦|B| である．

次に f: ω→C が単射で f∈U とする． f のsupportを E とする． E = C₀∪…∪C_n-1 としてよい． f が単射だから，ある m∈ω が存在して f(m) ∉ E となる．簡単のため， f(m) = c_k1 とする． k≧n である．このとき g∈G を g|_E = id，g|_Ck=α₂ とすれば g(f) = f だから

c_k1 = f(m) = g(f)(m) = g(f(m)) = g(c_k1) = α₂(c_k1) = c_k2

となり矛盾する．

以上により

定理 線型空間の基底の濃度の一意性は ZFA で証明できない．