選択公理とは，非空集合の族は 選択関数f: Λ→を持つという命題だった．このとき，Λや各X_λに制限を加えたものを考えることもできる．

これらは，AC_<などのような簡単な場合を除けばZFでは証明できないようだ． 例えばAC(2)はZFで証明できない(Jech『The Axiom of Choice』p71参照)など．

命題1AC(2)⇔AC(4)

証明(⇒) を4元集合の族とする． λ∈Λに対しA_λ := { Z⊂X_λ | |Z|=2 } と置く． A := ∪_{λ∈Λ}A_λと置けば，Aの各元は二元集合だからAC(2)により選択関数 f: A→∪_{Z∈A}Z=を持つ． λ∈Λとして，x∈X_λに対し n_{λ, x} := | { Z∈A_λ | f(Z)=x } | と置く．これは Σ_{x∈X_λ}n_{λ, x} = 6 を満たす． m_λ := max{ n_{λ, x} | x∈X_λ } と置いて Y_λ := { x∈X_λ | n_{λ, x}=m_λ } とする． |X_λ| = 4 と Σ_{x∈X_λ}n_{λ, x} = 6 により1≦|Y_λ|≦3が成り立つ． g: Λ→を

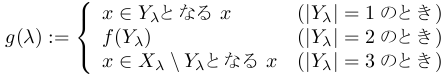
で定めればgが選択関数である．

(←) を2元集合の族とする． λ∈Λに対しA_λ := X_λ×{0, 1}と置けば |A_λ|=4だからAC(4)により選択関数 f: Λ→∪_{λ∈Λ}A_λが存在する． そこでπを第一成分への射影として g := πf: Λ→ とすれば明らかにgが選択関数である．

命題1の←は明らかに次のように一般化できる．

命題2正整数k, nに対し AC(kn)⇒AC(n)．

一般に AC(m)⇒AC(n) は成立するとは限らない．例えばm=2のとき， AC(2)⇒AC(n) が成立するn>1はn=2, 4だけであることが知られている． これにより AC(4)⇒AC(3) が成立しないことも分かる．何故ならば，成立すると仮定すると AC(2)⇔AC(4) により AC(2)⇒AC(3) が成立してしまい，矛盾するからである．

命題1の⇒は以下のように一般化され，命題5を得ることができる．

補題3pを素数，n>pをpの倍数としてAC(p)を仮定する． このときn元集合の族に対し 集合族{Y_λ}_λ∈Λで各λ∈Λに対し ∅≠ Y_λ ⊊ X_λとなるものが存在する．

証明A_λ := { Z⊂X_λ | |Z|=p } と置き A := ∪_λ∈ΛA_λとする． Aの各元はp元集合だからAC(p)により選択関数 f を持つ．

λ∈Λとする．x∈ X_λに対し n_{λ, x} := | { Z∈A_λ | f(Z)=x } | とする． m_λ := max{ n_{λ, x} | x∈X_λ } と置く． Y_λ := { x∈X_λ | n_{λ, x}=m_λ } と置けば ∅≠ Y_λ⊂ X_λである． このときY_λ≠X_λが成立する

|A_λ|=_nC_pであるから Σ_{x∈ X_λ}n_{λ, x} = _nC_p = n(n-1)…(n-p+1)/(p!) となる． n-1, …, n-p+1はpで割れないから Σ_{x∈X_λ}n_{λ, x}はnで割り切れない． よって「任意のx∈X_λに対しn_{λ, x}=m_λ」はありえない． 故にY_λ≠X_λである．

補題4nを正整数とする． 「任意の素数p≦nに対しAC(p)が成り立つ」ならば「任意の正整数k≦nに対しAC(k)が成り立つ」．

証明nについての帰納法．n=1のときは明らか．n>1とする． 任意の素数p≦nに対しAC(p)が成り立つとする． 帰納法の仮定により任意の1≦k≦n-1に対しAC(k)が成り立つ． 故にAC(n)を示せば証明が終わる．

(i) nが素数のとき．仮定によりAC(n)が成り立つから示すべきことは何も無い．

(ii) nが合成数のとき．AC(n)を示すため，をn元集合の族とする． 1≦k≦n-1に対しA_λ^(k) := { Z⊂X_λ | |Z|=k } と置き A^(k) := ∪_λ∈ΛA_λ^(k)とする． AC(k)をA^(k)に適用して 選択関数 f^(k) を得る．

nを割る最小の素数をpとすると，補題3により 集合族{Y_λ}_λ∈Λで各λ∈Λに対し ∅≠Y_λ⊊ X_λとなるものが取れる． 勿論1≦|Y_λ|≦n-1である．そこで f(λ) := f^(|Y_λ|)(Y_λ) と置けばfがの選択関数である． 故にAC(n)が成り立つ．

命題5nを正整数とする． 「任意の素数p≦nに対しAC(p)が成り立つ」ならば「任意の合成数k≦2n+1に対しAC(k)が成り立つ」．

証明補題4により任意の1≦m≦nに対しAC(m)が成り立つ．

k≦2n+1を合成数とする．AC(k)を示すため，をk元集合の族とする． 1≦m≦nに対しA_λ^(m) := { Z⊂X_λ | |Z|=m } と置き A^(m) := ∪_λ∈ΛA_λ^(m)とする． AC(m)をA^(m)に適用して選択関数f^(m)を得る．

kを割る最小の素数をpとすると，明らかにp≦nだからAC(p)が成り立つ． よって補題3により 集合族{Y_λ}_λ∈Λで各λ∈Λに対し ∅≠Y_λ⊊ X_λとなるものが取れる． 勿論1≦|Y_λ|≦k-1≦2nである．そこで

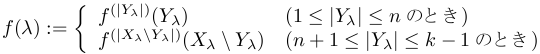
と置けば f がの選択関数である．故にAC(k)が成り立つ．

命題5でn=2とすれば先の AC(2)⇒AC(4) が得られる．またn=4とすれば AC(2)かつAC(3) からAC(6)，AC(8)，AC(9)が得られることが分かる．よって AC(2)かつAC(3) ⇔ AC(6) も分かる．

命題6AC(2)かつAC(5) ⇒ AC(8)

証明AC(2)とAC(5)を仮定する．命題1によりAC(4)が成り立つ．を8元集合の族とする． p=2として補題3を適用すると集合族{Y_λ}_λ∈Λで各λ∈Λに対し ∅≠ Y_λ⊊ X_λとなるものが存在する． 勿論1≦|Y_λ|≦7である．

次に自然数nに対しA_λ⁽ⁿ⁾ := { Z⊂X_λ | |Z|=n } と置き A⁽ⁿ⁾ := ∪_λ∈ΛA_λ⁽ⁿ⁾とする． AC(2)，AC(4)，AC(5)をそれぞれA⁽²⁾, A⁽⁴⁾, A⁽⁵⁾に適用して 選択関数f⁽²⁾, f⁽⁴⁾, f⁽⁵⁾を得る．

あとは，の 選択関数f: Λ→を

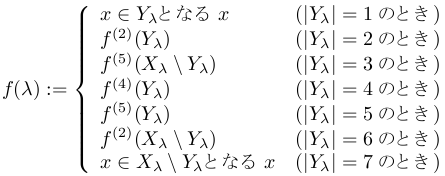
と定義すればよい．

命題7AC(10)⇒AC(8)

証明AC(10)⇒AC(2) と AC(10)⇒AC(5) により明らか．

命題8AC(3)かつAC(7) ⇒ AC(9)

証明AC(3)とAC(7)を仮定する． を9元集合の族とする．

自然数nに対しA_λ⁽ⁿ⁾ := { Z⊂X_λ | |Z|=n } と置き A⁽ⁿ⁾ := ∪_λ∈ΛA_λ⁽ⁿ⁾とする． AC(3)，AC(7)をそれぞれA⁽³⁾, A⁽⁷⁾に適用して 選択関数f⁽³⁾, f⁽⁷⁾を得る．

p=3として補題3を適用すると 集合族{Y_λ}_λ∈Λで各λ∈Λに対し ∅≠Y_λ⊊ X_λとなるものが存在する． 勿論1≦|Y_λ|≦8である．

|Y_λ|=4となるλ∈Λを取る． B_λ := { Z⊂Y_λ | |Z|=2 } と置く． Z∈B_λとするとX_λ＼Z∈A⁽⁷⁾だから g(Z) := f⁽⁷⁾(X_λ＼Z)∈X_λを考えることができる． そこでW_λ := { g(Z) | Z∈B_λ }⊂X_λと置く． |B_λ|=6だから1≦|W_λ|≦6である．

(i) |W_λ|=4とする．このとき

V_λ := { g(Z) | あるZ'∈B_λが存在してZ≠Z', g(Z)=g(Z') }⊂X_λ

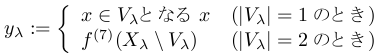
と定める．

(ii) |W_λ|=5とする．このとき

V_λ := { g(Z) | あるZ'∈ B_λが存在してZ≠Z', g(Z)=g(Z') }⊂X_λ

と置けば|B_λ|=6だから|V_λ|=1となる． そこでy_λ∈X_λをx∈ V_λとなるxにより定める．

(i)(ii)に注意して，x_λ∈ X_λを

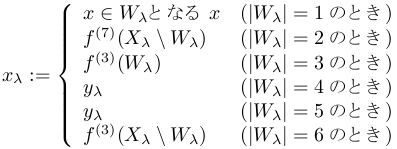
で定義する．

|Y_λ|=5となるλ∈Λの場合も X_λ＼Y_λに対して同様の議論をして x_λ∈X_λを定めておく．

あとは，の選択関数f: Λ→を

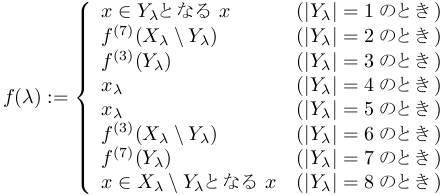
と定義すればよい．

命題9AC
⇔非空集合の族{ X_n }_n∈Nに対し，ある無限集合M⊂Nが存在してΠ_n∈M X_n≠∅

証明(⇒)明らか

(←) Y_m := Π_n=0^m X_nと置く．各Y_mは空でない．{ Y_m }_m∈N に仮定を適用すると， ある無限集合 M⊂N が存在してΠ_m∈M Y_m≠∅となる． 即ち元( y_m )_m∈M∈Π_m∈M Y_mが取れる． y_m∈Y_m=Π_n=0^m X_nだから y_m = < x₀^m, x₁^m, …, x_m^m> と書ける． そこで m(n) := min{ m∈M | n≦m } と置けば (x_n^m(n))_n∈N∈Π_n∈N X_nである．